Es ist schon ein klein wenig laenger her, als ich den ersten Teil schrieb, in dem ich mich eher in einem „meta-Sinne“ ueber den Kommentar (in Artikellaenge) von Shizuyo Sutou in Genes and Environment, 40 (article number 26), 2018 mit dem Titel „Low-dose radiation from A-bombs elongated lifespan and reduced cancer mortality relative to un-irradiated individuals„ ausliesz.
Es waren dann erstmal andere Sachen zu tun und auch keine Lust vorhanden das hier zu schreiben. Nun sitze ich aber gerade (und noch eine Weile) im Zug und habe zwar immer noch keine Lust … aber auch nix anderes zu tun. Selbstueberredung sei dank folgt dem ersten Teil endlich mal der zweite Teil.
Zunaechst sollte ich sagen, was Hormesis ist:
Hormesis is a two-phased dose-response relationship to an environmental agent whereby low-dose amounts have a beneficial effect and high-dose amounts are either inhibitory to function or toxic.
Das ist uns (also euch, meinen lieben Leserinnen und Lesern und mir) hier im Weblog auch schon begegnet, wenn auch in „umgekehrter Form“: lange wurde angenommen, dass Alkohol „hormetisch“ ist; kein oder zu viel Alkohol sind schlecht, das „richtige“ Masz aber ist gut … der Widerlegung dieser dummen „Volksweisheit“ widmete ich eine eine eigene Miniserie und werde deswegen nicht (nochmal) naeher darauf eingehen.
Meine erste persønliche Erfahrung mit einem „hormetischen Stoff“ hatte ich in Form einer Frage die mich sehr beunruhigte. Als naemlich der junge Mann der bei mir wohnt noch nicht geboren war, sein ganz individueller Phaenotyp sich aber schon kraeftig aus dem (ebenso individuellen) Genotyp entwickelte, poppte in meinem Gehirn pløtzlich die Frage auf: .o(Ach du Schreck! Woher weisz der neue Mensch denn, dass er sofort nach der Geburt alleine atmen muss?).
Die Antwort liegt im Kohlenmonoxid. Das ist naemlich ein Neurotransmitter und wenn von dem zu viel im Blut ist (weil man bspw. nicht atmet), dann startet das „Froschgehirn“ den Atemreflex. Das heiszt also, dass dieses Molekuel in kleinen Dosen nuetzlich fuer den Kørper ist, waehrend es bekannterweise in groszen Dosen vergiftend wirkt.
Und nun endlich zu dem worueber das erwaehnte Kommentar eigtl. handelt: (sehr) (leichte) Radioaktivitaet fuehrt zu weniger Krebstoten.
Wie erwaehnt fuehrt Sutou eine Vielzahl (meiner Meinung nach durchaus plausibler) Forschungsergebnisse an, warum dem so sein sollte. Und relativ kurz nachdem ich den Artikel angefangen hatte zu lesen, definitiv noch bevor ich meine Meinung diesbezueglich modifizierte, poppte in meinem oben erwaehnten Gehirn die Idee eines Mechanismus auf, wie das sein kønnte … und der geht (ganz grob und vereinfachend) so:
– Krebszellen sind (im Wesentlichen) unsterblich, die (hier ebenso bereits thematisierte) Apoptose funktioniert nicht richtig, weil die dafuer nøtigen Gene „kaputt“ sind;
– es ist aber so, dass Apoptose auch von den Mitochondrien eingeleitet werden kann;
– wenn nun ein bisschen Strahlung die (Krebs)zelle noch ein bisschen mehr kaput macht, kønnte das gerade ausreichen, dass die Mitochondiren aktiv werden und den Zelltod einleiten, obwohl die (Zellkern)Gene dafuer ausgeschaltet sind;
– das fuehrt dann dazu, dass Krebszellen absterben, bevor sie sich massiv vermehren und zu einem Problem werden;
– gesunde Zellen werden natuerlich auch geschaedigt, aber weil die Apoptose dort richtig funktioniert sterben die einfach nur ab und es macht fuer den Gesamtorganismus keinen Unterschied ob das nun wegen wenig Strahlung oder wegen was anderem war;
– das Ganze ist natuerlich ein Prozess der selber auch zu Krebs fuehren kann, wenn die Strahlung ueberhaupt erste besagte „Apoptosegene“ kaputt macht;
– aber es gibt urst URST viel DNA-„Material“ was scheinbar (anscheinend?) ueberhaupt keine Funktion hat (also bspw. (und meistens) nicht in Eiweisze ausgedrueckt wird) und Strahlung „trifft“ auf die DNA rein statistisch und bei geringer Strahlung ist es wahrscheinlicher, dass ein Bereich der DNA getroffen wird, bei dem das nicht so schlimm ist und unwahrscheinlich, dass ein „Apoptosegen“ beschaedigt wird;
– nun ist die Zelle aber groeszer als der Zellkern und es kønnte sein, dass (geringe) Strahlung in ihr rein statistisch gesehen etwas haeufiger ’ne Sache kaputt macht, die dann die Mitochondiren alarmiert und manchmal ist das dann ’ne Krebszelle;
– das Ganze hørt bei Strahlungsdosen die nicht mehr als gering (!) bezeichnet werden kønnen auf zu funktionieren, einfach weil die Chance „gute DNA“ zu „treffen“ (und damit zu veraendern) sich vergrøszert, waehrend (mglw.?) die Chance „irgendwas in der Zelle kaputt machen“ nicht im gleichen Masze zu nimmt;
– so weit so gut … nun ist es auch so, dass die Erde (viel) frueher etwas mehr radioaktiv war, als sie es heute ist … es wuerde mich also nicht wundern, wenn damals die ersten DNA enthaltenden Organismen sich so entwickelten, dass es insgesamt von Vorteil war mehr „unnuetze DNA“ mit sich „rumzuschleppen“ um etwas bestaendiger gegen besagte Strahlung zu sein;
– damals fuehrte das zwar zu weniger mutierten Zellen, aber weil das so frueh in der Evolution entstanden ist, ist es so sehr in den „Funktionsprinzipien der DNA“ (und damit des ganz allgemeinen Lebens) eingebaut und deswegen ist das immer und ueberall sowieso da und zaehlt somit nicht wirklich zum besagten Mechanismus sondern ist eher eine Art „evolutionaer verminderte Krebsbasisrate“;
– die Mitochondiren kamen spaeter dann dazu und uebernahmen eine wichtige Rolle bei der Apoptose … dazu gehørt Zeichen zu erkennen wann eine Zelle beschaedigt ist … Letzteres ist das was (geringe) Strahlung macht;
– und ich merke gerade, dass ich anfange immer nur ueber die gleichen Sachen zu reden, nur von anderen Blickwinkeln gesehen.
Lange Rede kurzer Sinn: ich konnte es mir das also durchaus vorstellen, dass geringe Strahlung die Krebsraten (leicht!) vermindert. Sutou bringt dann im Artikel auch selbst das Argument der erhøhten Strahlung auf der juengeren Erde und dass es sinnvoll ist anzunehmen, dass die Evolution dafuer sorgte, dass uns das nicht uebermaeszig kaputt macht.
Dass ich die Idee dann selber hatte, half vermutlich unterbewusst, dass es mir leichter viel auch den Rest der Ergebnisse (nach genauem Anschauen und etwas drueber Nachdenken) zu akzeptieren und letztlich meine Meinung wesentlich zu aendern.
Und nun ist der Beitrag schon wieder so lang. Eine Sache fehlt aber noch und die handelt darueber, warum das zwar (vermutlich) alles richtig ist, ich damit aber abseits der wissenschafltich (im Uebrigen hochinteressanten) Diskussion dennoch ein Problem habe. Oder anders: Fortsetzung folgt.
Nach den vielen leckeren Sachen in den letzten Beitraegen (und dem einen Gemuese, welches frueher nicht lecker war, es aber mittlerweile ist) … die eigentlich alle das Gleiche Gruenzeug sind … heute nun der letzte Beitrag in dieser Reihe.
Der Titel verraet es schon: es geht um den Gruenkohl und obwohl das letztlich auch nur ’n Blumenkohl ist, so fand ich den schon immer (und finde den immer noch) voll UNlecker. Egal ob pueriert, im Ofen gerøstet, in der Pfanne „gebraten“, oder in irgendeiner anderen Form. Gruenkohl bringt’s einfach nicht, selbst wenn er zur Familie der Brassica oleracea gehørt, wie all die vorherigen leckeren Sachen.
Es lohnt sich durchaus letzterem Link mal zu folgen, denn der hat ’ne Liste mit noch mehr Blumenkohlkultivaren von denen ich noch nie gehørt habe (sowas wie Kai-lan oder Jersey cabbage).
Nur eins kann man dem Gruenkohl zu gute halten: es ist wenigstens keine Zucchini (oder Aubergine) … dem Zeuch steh ich naemlich so widerstrebend gegenueber, dass ich da nicht mal drauf verlinken will.
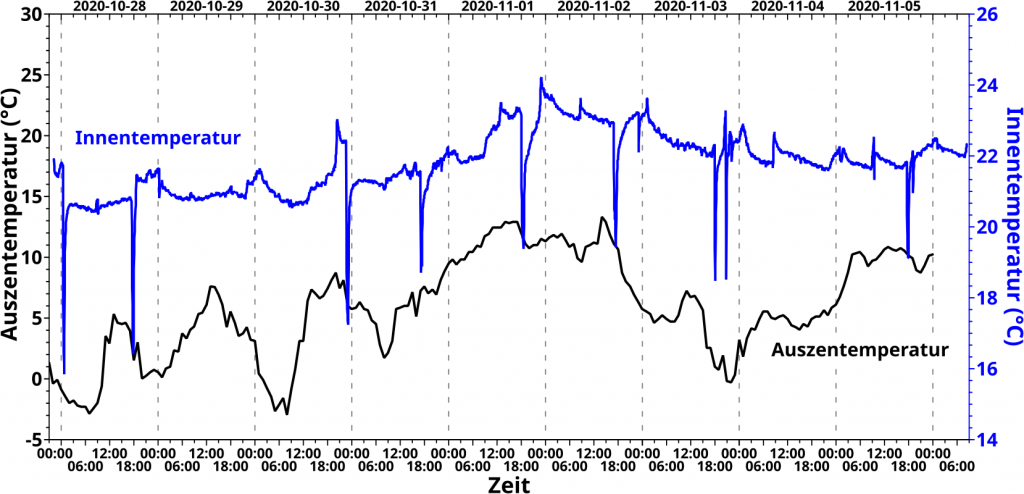
Eine Sache hatte ich bisher mit Absicht auszen vor gelassen, es waere aber unehrlich da nicht drauf einzugehen: die (allgemeine) „Kurvenform“ der Temperaturkurve. Diese hat naemlich nicht nur die besprochenen „herausstechenden“ Merkmale wenn ich bspw. ein Fenster øffnete oder den Herd anmachte, sondern da ist ueber den gesamten Messzeitraum auch eine „mittelfristige“ Veraenderung zu erkennen. Die ersten ca. 3 1/2 Tage blieb die „mittlere“ (so Pi mal Daumen, aber doch gut mit dem Auge zu erkennen) Temperatur relativ stabil um ca. 21 °C … eine feine Innentemperatur. Dann stieg sie innerhalb eines Tages auf ca. 23 °C an. Auf diesem Niveau „verharrte“ die Temperatur fuer ca. 1 1/2 Tage um dann innerhalb ca. eines Tages wieder auf 22 °C abzufallen und dort zu verbleiben fuer den Rest des Messzeitraums.
Zur Erklaerung muss man die Auszentemperatur heranziehen und ich habe die beiden Temperaturen in diesem Diagramm zusammen aufgetragen:
Die linke Ordinate ist fuer die Auszen- und die rechte Ordinate fuer die Innentemperatur … man beachte die unterschiedlichen Skalen.
Zunaechst muss ich sagen, dass ich die Auszentemperaturdaten nicht selber aufgenommen, sondern vom norwegischen Klimaservicezentrum habe. Leider gibt es fuer den Messzeitraum keine Daten fuer die Wetterstation in unmittelbarer Naehe zu mir. Ich habe aber die Daten einer anderen Wetterstation genommen, welche nicht all zu weit weg liegt (aus der Vogelperspektive). Das ist nicht so schlimm, denn ich bin hier ohnehin nicht an den ganz genauen Werten interessiert sondern nur wie warm (bzw. kalt) es insgesamt war.
Ich gehe nun wieder ins Detail und zunaechst schauen wir auf die ersten drei Tage. Hier zeigt die Auszentemperatur charakteristische Tag- und Nachtschwankungen; es wird waermer wenn’s hell ist und kaelter nach Sonnenuntergang.
Wenn man die ersten drei Tage genau hinschaut, dann scheint die Innentemperatur diesem Trend zu folgen, denn dort gibt es eine Art „zick-zack-Muster“ mit einer Periode von ungefaehr einem Tag und einem maximalen Temperaturunterschied von ca. 1/4 °C … wobei das natuerlich sehr „verwaschen ist und „menschengemachte Sachen“ „darueber liegen“.
Weiter is zu den ersten drei Tagen zu bemerken, dass die Nacht(auszen)temperaturen um ca. 0 °C liegen und die Tages(auszen)temperaturen bei ca. 5 °C.
Ab ungefaehr der Mittagszeit am 220-10-31 høren diese Tag- und Nachtschwankungen auf und die Auszentemperatur steigt in der Nacht und bis zum Mittag des darauffolgenden Tages auf fast 13 °C an um dort einen weiteren Tag (auch ueber Nacht) zu bleiben. Am Abend des 2020-11-02 war mit dem warmen Wetter Schluss und die Temperatur faellt innerhalb eines Tages wieder auf ca. 0 °C ab. Die Temperatur macht dann aber auch sofort wieder eine Kehre und steigt (mehr oder weniger gleichmaeszig und auch ueber Nacht) innerhalb eines Tages wieder auf ca. 10 °C an und verbleibt dort bis zum Ende der Messperiode..
Wie oben schon besprochen, zeigt die Innentemperatur ein aehnliches Verhalten, es „fehlt“ nur die starke Abkuehlung um den 2020-11-03 herum.
Worauf ich hinaus will, ist dass hier etwas vor sich geht und meine Innentemperatur vermutlich von der Auszentemperatur beeinflusst wird. … … … Das ist jetzt natuerlich keine so richtig ueberwaeltigende Aussage, denn alle die ’ne Whg. haben wissen, dass es im Sommer auch ohne Heizung in der Stube warm wird.
Bei mir scheint aber ein weiterer Faktor dazu zu kommen und die Erklaerung scheint nicht nur die uebliche, rein thermodynamische Waermeuebetragung vom „Auszenreservior“ in den Innenraum durch eine isolierende Schicht hindurch, zu sein. Dieser Faktor ist das Haus an sich denn ich habe den Eindruck, dass es „atmet“. Oder anders: hier wird viel mit Holz gebaut und wenn es wirklich kalt ist ein paar Tage, dann verzieht sich alles so sehr, dass sogar der Zigarettenrauch meiner ueber mir wohnenden Vermieter zu mir runter zieht.
Mein Eindruck (relevant fuer den vorliegenden Fall) ist, dass bei ueber 5 °C alle Ritzen (vermutlich durch thermische Ausdehnung (?)) fest verschlossen sind und die Waerme (fast) komplett drinnen bleibt. Das Waermesystem meiner Whg. (also nicht nur die Fuszbodenheizung an sich (auch wenn die dominiert), sondern auch alle Møbel die im thermodynamischen Gleichgewicht sind und natuerlich auch der Fernseher, die PlayStation, der Laptop, der Ofen usw. usf.) ist urst traege und braucht immer ’n Tag (so Pi mal Daumen) um sich auf eine Situation neu einzustellen.
Was hier jetzt also passiert ist das Folgende: in den ersten drei Tagen „steckt etwas mehr Energie im System“ als bei rein thermodynamischer Waermeuebertragung (usw., siehe oben) benøtigt wird um die angenehmen 21 °C zu halten. Dies natuerlich, weilder Waermeverlust durch die Ritzen permanent auszugleichen ist (daher uebrigens die Metapher des „Atmens“, denn die meiste Waerme geht in Form „durch-die-Ritzen-ausgepuster“ warmer Luft verloren). Durch den pløtzlichen Wetterumschwung sind die Ritzen dann aber pløtzlich dicht und auch wenn die Heizung nicht mehr heizt, so ist doch das bisschen mehr an Energie noch da und die kommt nun nicht mehr (so schnell) „raus“ und die Innentemperatur steigt an und „verharrt“ dann zwar nicht bei ca. 23 °C (wie ich oben schrieb) nimmt aber nur langsam ab.
Als die Auszentemperatur dann in der Nacht des 2020-11-02 wieder abnimmt geht sie dennoch nur kurz in der darauffolgenden Nacht unter die „magische Schwelle“ von ca. 5 °C. Dieser kurze Zeitraum reicht aber nicht aus um die Ritzen lange genug zu øffnen um wieder auf 21 °C zurueck zu kommen … und dann ist’s drauszen auch schon wieder 5 °C und waermer und das Innensystem hat sich auf das neue „alle-Ritzen-sind-zu-wir-muessen-nicht-so-dolle-Energie-zufuehren-weil’s-sonst-zu-warm-wird“-Gleichgewicht eingepegelt.
So … nun ist das erklaert und ja das hat jetzt zwar alles nichts mit Feinstaubmessungen zu tun, aber es zeigt doch (eindrucksvoll … ? … zumindest sehr praktisch) wieviel bei Messungen unter Realbedingungen passiert, was dann die Ergebnisse beeinflusst.
Beim naechsten Mal gibt’s dann Drauszenmessungen und ich erklaere warum ich das hier so kleinteilig erklaert habe (mal davon abgesehen, dass das durchaus spannend an sich ist).
Als ich mich das erste Mal mit der Verteilung der Laenge der Wikipediaartikeltitel beschaeftigte, simulierte ich sehr viele Namen um etwas genauer zu untersuchen und meinte beim letzten Mal bzgl. der Simulation:
Auch wenn ich das Programm dazu gerade nochmal neu schreibe, werde ich das hier nicht wiederholen, denn diese Simulation war von externen Daten abhaengig und wuerde heute genauso ausfallen.
Und damit lag ich zwar nicht komplett daneben … es war aber auch nicht ganz richtig, denn ich kam sehr wohl auf andere Ergebnisse. Dazu weiter unten mehr.
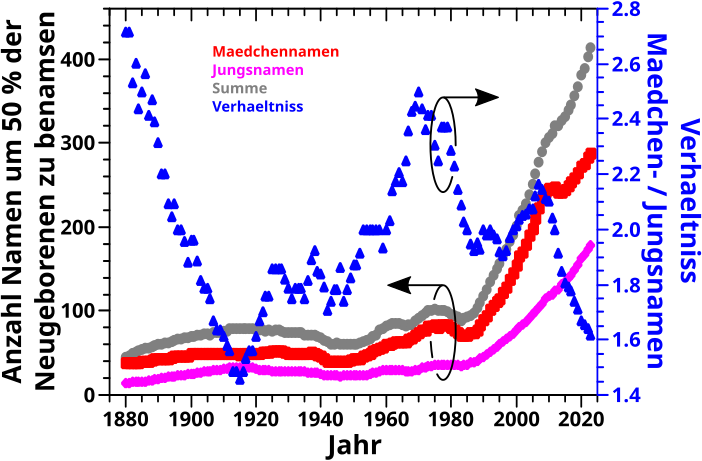
Zunaechst møchte ich aber nochmal darauf eingehen, wieviele Vornamen man braucht um 50 Prozent aller Babies einen Namen zu geben (wenn diese nach der Beliebtheit ihrer Vornamen sortiert werden). Das war selbst mir zu periphaer vor drei Jahren und ich hatte das deswegen in den damaligen Geburtstagsbeitrag ausgelagert (ich meine das zweite Bild). Dabei hatte ich aber nur Daten betrachtet die „ueber alle Babies gehen“ (also eine Art „Summensignal“).
Jetzt beim Neuschreiben der Programme fuegte ich eine Funktion ein, welche mir auch die zwei Teile dieses „Summensignals“ separat ausspuckt. Oder anders: ich habe jetzt auch nach Maechen und Jungs getrennte Ergebnisse und das sieht so aus:
Das „Summensignal“ (graue Punkte) ist das Selbe wie beim vor drei Jahren (auszer, dass drei weitere Jahre dazugekommen sind). Ich fand es aber erstaunlich, dass die Variation bei den Maedchennamen immer ca. 1.5 bis fast 3 Mal grøszer ist (siehe die blauen Punkte). Maedchennamen machen also den Hauptteil am Summensignal aus und deswegen bringe ich das hier doch nochmal, denn das habe ich ja damals ueberhaupt nicht gesehen.
Nun stellt sich natuerlich die Frage warum das so ist, welche ich hier aber nicht beantworten kann (einfach weil ich’s nicht weisz und nicht wuesste wie ich an entsprechende Daten kommen kønnte). Aber zwei potentielle Ursachen fallen mir ein. Zum Einen, kønnten Jungs staerker irgendwelchen Namenstraditionen unterliegen als Maedchen; der Uroppa hiesz schon so und deswegen heiszt der Enkel auch so. Zum Anderen kønnte es aber auch sein, dass es mglw. mehr Maedchennamen als Jungsnamen gibt; der „Maedchennamentopf“ ist also „grøszer“. Das wuerde nicht mal unbedingt mit dem Anstieg ab ca. Mitte der 80er Jahre im Konflikt stehen, denn das Verhaeltniss der Namen bleibt (so ungefaehr) das Gleiche. Besagter Anstieg haengt mglw. mit dem demographische Wandel in den USA zusammen, was zu einem (viel) mehr an Namen fuehrt. Aber dieses „Mehr an Namen“ verteilt sich (mehr oder weniger) gleichmaeszig ueber Jungs- als auch Maedchennamen.
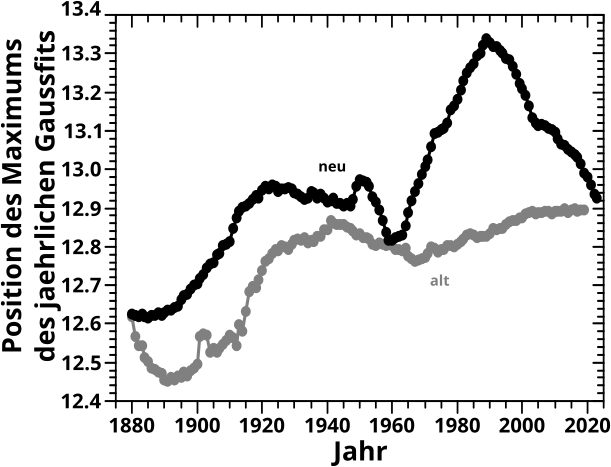
Das war das Ergebnis das sich nicht aenderte. Im gleichen Geburtstagseintrag zeigte ich aber auch die Parameter der Gausskurven fuer jaehrliche Simulationen … und die haben sich geaendert. Hier sieht man das fuer die Position des Zentrums …
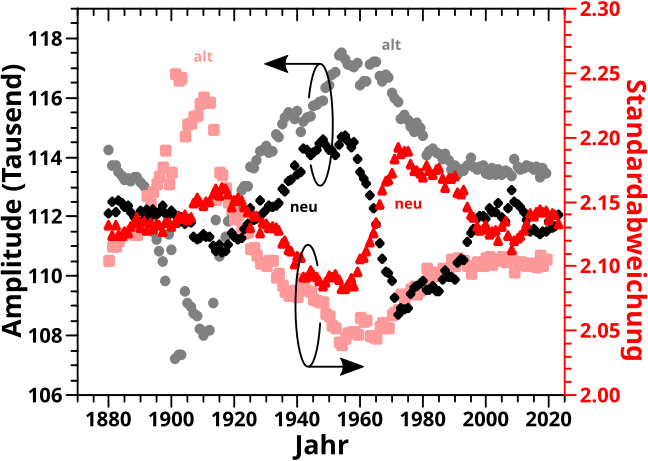
… welches im Mittel jetzt sogar noch besser mit dem beim letzten Mal erwaehnten „Hauptprozess“ uebereinstimmt … und hier fuer die Amplitude und Standardabweichung besagter jaehrlichen Gaussfits:
Zum Glueck liegen die Ergebnisse nicht nur in der selben Grøszenordnung, sondern auch innerhalb des selben (sehr engen) Bereichs. Auszerdem sind die allgemeinen Merkmale (wann die Kurven hoch oder runter gehen bzw. so ungefaehr gleich bleiben) im Wesentlichen auch die Gleichen. Ja es gibt Abweichungen (die ja auch der Grund sind, warum ich das hier doch nochmal bringe) aber weil sich das alles ohnehin in sehr engen (Zahlen)Bereichen befindet sind sowieso nur die grøszeren Trends von Interesse und deswegen aendert sich an meinen damaligen Aussagen nix.
Aber es machte mich natuerlich sehr stutzig, dass bei gleichen Ausgangsdaten (zur Erinnerung: fuer diese Simulationen benutzte ich externe Namensdaten und nicht die Wikipedia und an denen hat sich nix geaendert seit 2021) und eigentlich (und auch uneigentlich) gleicher Methode ueberhaupt etwas anderes raus kam.
Es stellte sich heraus, dass der Fehler bei mir lag. Zur Erinnerung: beim zufaelligen „Ziehen“ von Namen aus dem groszen Namenstopf war die Wahrscheinlichkeit einen bestimmten Namen zu ziehen davon abhaengig wie oft der (im jeweiligen Jahr) an Babies vergeben wurde. Fuer 1880 gab es also viele Marys und Johns im Namenstopf, aber nur sehr wenige Wilmas und Zachariahs.
Wie oft ein Name im Topf vorkommt berechnete ich nun so, dass ich die Anzahl der Babies mit einem gewissen Namen durch die Anzahl aller Babies teilte (so weit so gut) und dann mit der Anzahl der Namen die ich insgesamt simulieren wollte multiplizierte (immer noch so weit so gut). Aber weil ich bei meinem selbtgeschriebenen „Namen-aus-dem-Topf-zieh“-Algorithmus nur mit ganzen Zahlen arbeiten konnte, hab ich bei dezimalen Wahrscheinlichkeiten einfach alles nach der ganzen Zahl abgeschnitten. Fuer Namen die im Namenstopf oft genug vorkommen macht das keinen groszen Unterschied. 23517.5 ist nicht viel anders als 23517 … das kann man sogar fuer 10.9 noch argumentieren … mglw. sogar noch fuer 5.5 oder auch fuer 3.9 (selbst hier ist der Fehler ja nicht mal 25 %).
Aber bei all zu kleinen Zahlen kann das Abschneiden der Dezimalstellen im Groszen und Ganzen zu Problemen fuehren, denn es gibt recht viele Namen die bei meinem „selbstgestrickten“ Algorithmus nur ein- oder zweimal im Namenstopf waren und deswegen im Extramfall nur halb so oft gezogen wurden, wie sie haetten gezogen werden sollen.
Beim nochmal Neuschreiben des Programms habe ich das nicht nochmal selbst geschrieben, sondern geschaut was in den vielen umfangreichen Mathebibliotheken von Python zu finden ist und ein entsprechendes Modul benutzt. Besagtes Modul macht alles richtig und deswegen sieht es jetzt anders aus, weil die „Ziehwahrscheinlichkeit“ nun auch fuer sehr selten vorkommende Namen richtig ist.
Zum Glueck ist es aber so, dass sehr selten vorkommende Namen nur sehr selten gezogen werden (selbst wenn mein erster Algorithmus die sogar noch seltener gezogen hat) und deswegen sind die ersten Ergebnisse nicht komplett falsch sondern nur im Detail.
So, das soll jetzt dazu reichen und ich verbleibe wie beim letzten Mal:
[…] wenn ich das richtig sehe, dann gibt’s beim naechsten Mal nicht so viel zu schreiben … aber ich sollte lieber nix versprechen, was ich vermutlich nicht halten kann.
Aus Kyoto springen wir nochmals in den Norden nach Sapporo denn nicht nur sind dort einige Haeuser … nun ja, mindestens eins … mit Zahlen zum besseren Zaehlen versehen, sondern es gibt auch (mindestens eine) Treppe(n) die die verbrauchten Kalorien zaehlen:
Ich versuche ohnehin immer die Treppen zu nehmen … mit der Einschraenkung, dass ich bei fuenf Stockwerke die Grenze ziehe … oder wenn ich schwere Dinge bei mir habe … oder wenn es eine Rolltreppe gibt, denn die sind viel zu spassig um die nicht zu benutzen.
Im Wesentlichen mache ich das wg. des selben Hintergrunds warum hier die „verbrannten Kalorien“ angezeigt werden. Das hatte den schønen Nebeneffekt, dass ich mir das Treppensteigen waehrend der Coronapandemie nicht erst 0angewøhnen musste.
Worauf ich aber hinaus will ist, dass es selbst mich noch mehr motiviert die Treppe zu nehmen, wenn es einen Kalorienzaehler gibt und ich finde, dass es den bei allen Treppen geben sollte. Es ist naemlich voll fein sofort eine positive (wenn auch indirekte) „Bemerkung“ zu bekommen, wenn man was fuer die Gesundheit Gutes tut … und mglw. wuerde sich meine oben erwaehnte Grenze vllt. sogar ausdehnen auf sechs, sieben, oder vielleicht sogar noch mehr, Stockwerke, wenn as an allen Treppen angezeigt werden wuerde.
Und mehr gibt’s dazu auch gar nicht zu sagen :)
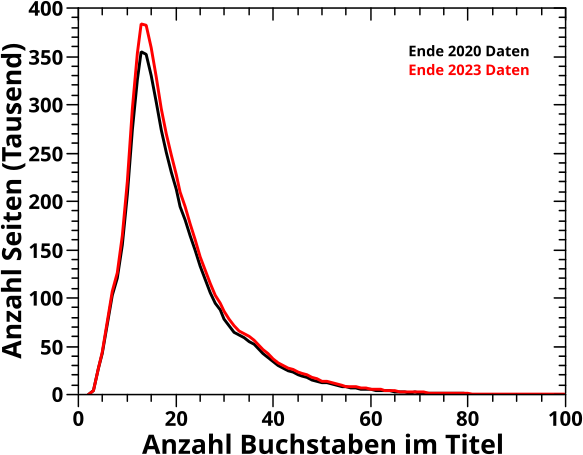
Ganz unabhaengig von der Linknetzwerkanalyse betrachte ich damals die Titellaengen etwas genauer. Hier von Interesse ist nur die Verteilung derselben und daran hat sich wenig geaendert:
Das Integral unter der Kurve ist jetzt etwas grøszer (entsprechend der Anzahl der dazugekommenen Artikel), aber die Form ist so sehr die Gleiche, dass es fast schon das Selbe ist … mhmm … sprachlich gesehen ist „fast das Selbe“ sowas wie „fast schwanger“ … also Quatsch … aber ihr, meine lieben Leserinnen und Leser wisst sicherlich worauf ich hinaus will … aber ich schwoff ab.
Wenn man annimmt, dass alle neuen Artikel sich im Durchschnitt wie alle bereits vorhandenen Artikel „verhalten“ (und das schlieszt die Artikeltitel ein) war das zu erwarten. Und dies ist eine sehr sinnvolle Annahme und jede andere Annahme muss SEHR gut begruendet sein! Natuerlich sind Abweichungen vom Durchschnitt denkbar. „Nichtdurchschnittlich“ ist es bspw., wenn in den drei dazwischen liegenden Jahren nur Artikel ueber chemische Verbindungen mit langen Namen neu hinzugekommen waeren. So eine Anomalie ist an sich natuerlich interessant, aber die Wahrscheinlichkeit dafuer ist gering und deswegen verteilen sich Laengen der neuen Artikeltitel im Wesentlichen so wie die alten.
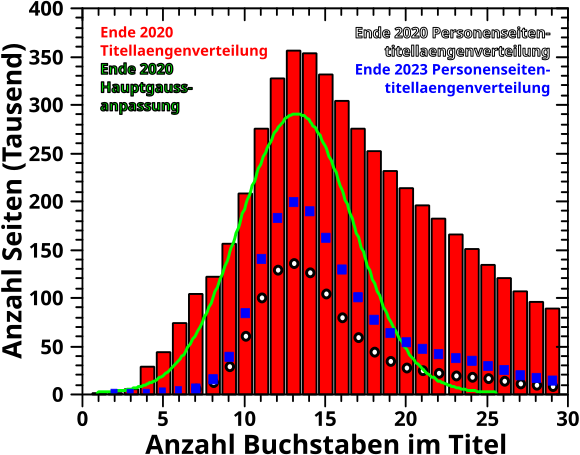
Damals konnte ich die Form der Verteilung mittels dreier (gaussverteilter) Prozesse anpassen. Fuer den staerksten dieser drei Prozesse versuchte ich die (Haupt)Ursache zu finden und landete letztlich auf Namen von (mehr oder weniger) beruehmten Leuten.
Dafuer simulierte ich vor drei Jahren zunaechst sehr viele Namen und konnte tatsaechlich (innerhalb vernuenftiger Grenzen) das Zentrum und die Amplitude des ersten erwaehnten Prozesses nachempfinden. Auch wenn ich das Programm dazu gerade nochmal neu schreibe, werde ich das hier nicht wiederholen, denn diese Simulation war von externen Daten abhaengig und wuerde heute genauso ausfallen.
Danach kam ich dann drauf mal zu schauen, ob es bei der Wikipedia vielleicht eine Kategorienseite mit links zu Seiten von Leuten gibt. Die gibt es, aber leider verteilen sich die fast 2 Millionen Seiten zu Leuten auf etlichen tausend Kategorien, weil die vielen Menschen alle fuer unterschiedliche Sachen beruehmt sind.
Einen leider nur halben Ausweg war die Kategorieseite aller lebenden Menschen. Halb deswegen, weil sich dort nur ca. 60 Prozent aller Seiten zu Leuten finden lassen. Das restliche Drittel sind schon verstorbene Menschen und die entsprechende Kategorieseite listet leider nicht die Links zu den Seiten sondern wieder nur die (vielen) Kategorieseiten unter die diese Leute fallen (fielen?).
Aber mit den 2/3 konnte ich zumindest eingeschraenkt arbeiten und die Verteilung der Titellaengen von Seiten zu lebenden Menschen hatte das Zentrum auch an der richtigen Stelle (weil aber so viele fehlten war die Amplitude nur halb so grosz wie die des erwaehnten Hauptprozesses).
Als ich die entsprechenden Programme nochmal schrieb, schaute ich wieder ueber viele Kategorieseiten und stolperte letztlich ueber die Kategorien Births per year und Deaths per year. Da sind die Leute zwar auch nicht direkt aufgelistet, aber die Links zu den Unterkategorien der Leute die in den entsprechenden Jahr geboren / gestorben sind ist systematisch und mit systematischen Sachen kann ich arbeiten.
Und siehe da …
… ich konnte die allermeisten Seiten zu Leuten finden (und nicht nur ca. 60 %). Das sind sicherlich immer noch nicht alle Seiten zu Leuten, denn Autoren muessen die in den entsprechenden Kategorien eintragen, aber ich wuerde schaetzen, dass mir weniger als 5 % fehlen.
Und das Gute ist, dass sich nicht nur das Zentrum nicht verschiebt, sondern die Amplitude der neuen Daten 2/3 der Amplitude des besagten staerksten Prozesses erreicht. Damit ist das Ergebnis nahe genug dran, dass das fuer sich selber spricht und ich das so stehen lassen kann und (anders als damals) nicht rumdiskutieren muss, warum ich denke, dass die Daten (trotz merklich kleinerer Amplitude) vermutlich dennoch richtig sind.
Genug fuer heute … wenn ich das richtig sehe, dann gibt’s beim naechsten Mal nicht so viel zu schreiben … aber ich sollte lieber nix versprechen, was ich vermutlich nicht halten kann.
Ich hab ’n Kollegen der ist urspruenglich auch aus Dtschl. Dessen Vater hatte ’n Hotel und (wenn ich das richtig verstehe) war deswegen bekannt mit Artur Fischer … der mit den Duebeln. Deswegen traf mein Kollege den auch manchmal und bei einem dieser Begegnungen hat er diese Autogrammkarte mit den Originalunterschriften der Apollo 11 Astronauten geschenkt bekommen:
Klar, die sind sicherlich zu hunderten, wenn nicht sogar zu tausenden verteilt worden an alle die irgendwie mit dem Apolloprojekt zu tun hatten. … … … und es wuerde mich nicht im Geringsten wundern, wenn Artur Fischer irgendwie an einer kleinen Sache mit dem Apolloprojekt zu tun hatte. Auch ist die Widmung sicherlich von wem anders geschrieben worden und das „Gesamtkunstwerk“ wurde den Astronauten dann nur zur Unterschrift vorgelegt.
Aber dennoch, die Signaturen sind echt (also nicht nur fotokopiert oder so) und damit hatten die zwei ersten auf dem Mond wandelnden Menschen und ihr nicht minder wichtiger … vermutlich sogar wichtigerer … im Mondorbit verbliebender Mitraumfahrer das in der Hand … und da ich das Foto mit den Unterschriften in der Hand hatte, folgt aufgrund transitiver Relationen, dass ich auch auf dem Mond war dem Mond (im uebertragenen Sinne) nun ein gutes gigantisches Stueckchen naeher bin als die meisten Menschen … fetzt wa!
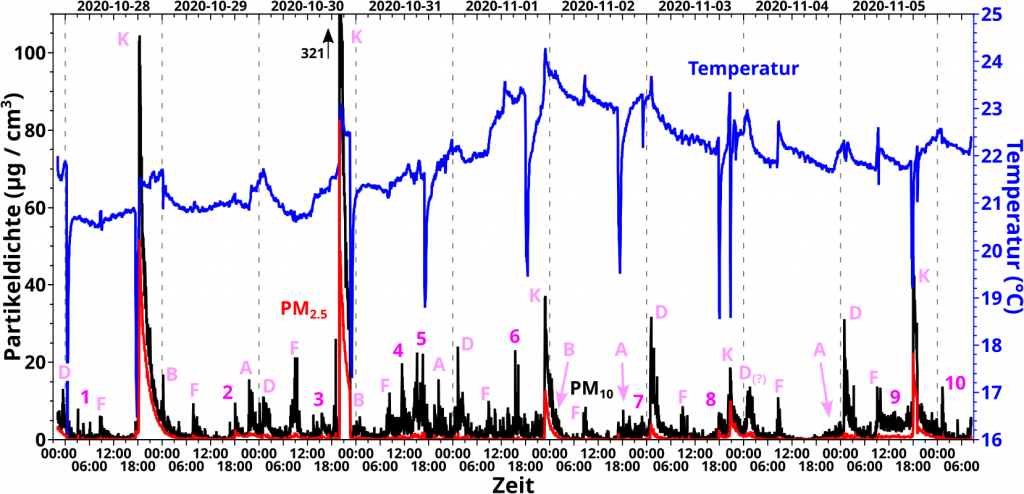
Beim letzten Mal wurde die letzte, mir bekannte Ursache fuer Feinstaub in der Kueche betrachtet. Zusammen mit den vorher behandelten Gruenden konnten damit im Uebersichtsdiagramm fast alle Spitzen erklaert werden. Aber eben nur fast, denn ein paar Ereignisse stehen weiterhin ohne Erklaerung da. Ich habe die hier mal mittels Zahlen gekennzeichnet und gehe die heute alle durch:
Die drei Spitzen bei der #1 muessen unerklaert bleiben. Ich habe keine Ahnung, was da zwischen nachts drei Uhr und morgens sechs Uhr passiert sein kønnte. Fluktuationen sind aber zu erwarten. Vielleicht ist ’ne Fliege vorbeigeflattert, oder der Kompressor des Kuehlschranks hat mal ungewøhnlich stark gerumpelt. Ich kann leider auch nicht sicher sagen, ob da auch immer was bei anderen Tagen (in dem selben Zeitraum) geschieht. Am Tag danach gibt’s eine kleine Spitze gegen 4 Uhr und am letzten vollstaendigen Messtag ist auch was gegen 3 Uhr (beide nicht gekennzeichnet). Aber bei allen anderen Tagen ist da entweder nix, oder wenn da was ist, dann geht das im „Reststaub“ von vorhererigen Kuechengeschehnissen unter. Ich muss also zugeben, dass ich das nicht aufklaeren kann.
Alle Spitzen von #2 bis #9 geschehen in Zeitraeumen zwischen 12 Uhr und dem Kochen des Abendmahls. Diese sind aber nicht regelmaeszig, bzw. mache ich da nix regelmaesziges in der Kueche, dem ich das zuordnen kønnte. Andererseits ist die Kueche auch ein hoch frequentierter Ort (vermutlich mehr als die Toilette); dort ist also immer was los. Und wenn ich da so mal drueber nachdenke, dann waere es eher verwunderlich, wenn in dem Zeitraum nix waere, denn wenn wer zu Hause ist, wir mal ’n Tee aufgebrueht, oder ’n Toast gemacht, oder man raeumt auf und wischt dabei den Tisch ab, oder der Einkauf wird in die Schraenke einsortiert etc. pp. Es sind aber alles so „kleine“ Sachen, dass die nicht mit einer groszen Staubentwicklung und auch mit keiner Waermeentwicklung einhergehen.
Im Gegensatz zu #1 sind das also keine mysteriøsen Geschehnisse, sondern einfach nur unterschiedliche aber gewøhnliche Kuechenaktivitaeten.
Die #10 ist ganz einfach, denn das sieht mir nach einer „Brotschmieraktivitaet“ aus und ich hatte das nur vergessen einzutragen, als ich solche Ereignisse besprach.
So … das war’s mit den Feinstaubmessungen in der Kueche, aber das war’s noch nicht insgesamt. Beim naechsten Mal gehe ich noch auf ein Merkmal der Temperturentwicklung ein, bevor ich mich kurz drauszen durchgefuehrten Feinstaubmessungen widme.
Wie erwaehnt fehlt in diesem Projekt noch eine grosze und wichtige Sache: sind die Ergebnisse reproduzierbar?
Diese Frage konnte natuerlich nicht mit den selben Daten beantwortet werden und deshalb lud ich mir Ende November 2023 die Wikipedia nochmal runter. Der Prozess war wie beim ersten Mal, nur dass drei Jahre mehr Daten drin waren. Deswegen ist die entpackte Datei nun ca. 90 GB grosz (die drei Jahre juengeren Daten sind „nur“ 75 GB grosz).
Alles was ich damals tat um die relevanten Daten aus der riesigen Datei zu popeln und diese fuer die eigentliche Linknetzwerkanalyse vorzubereiten, machte ich nochmal. Die Programme dazu liesz ich im Wesentlichen unveraendert (die sind jetzt nur besser strukturiert und der Code ist besser kommentiert).
Vor drei Jahren konnte ich die urspruenglichen 75 GB letztlich auf eine nur 1.4 GB grosze (Text)Datei reduzieren. Die Zahl gab ich damals nicht an und mit der Wikipedia vom November 2023 erhøhte sich die Grøsze dieser Datei nur auf 1.6 GB
Damals verblieb ich mit 5,798,312 Wikipediaseiten und 165,913,569 Links. Die neuen Daten enthalten 6,269,403 Seiten und 198,870,985 Links.
Das kønnen wir mit der beim letzten Mal vorgestellten Information vergleichen. Am Ende der Untersuchungsperiode kamen bei der Wikipedia ca. 13-tausend neue Seiten pro Monat dazu. Drei Jahre entsprechen 36 Monaten und somit ca. 468-tausend neuen Seiten. An den Zahlen oben sieht man, das es in echt 471,091 neue Seiten waren … das ist fast schon erschreckend, wie genau die relativ grobe Abschaetzung das abbildet.
Damit fuehrte ich vom Konzept die selbe Linknetzwerkanalyse durch. Im entsprechenden Code veraenderte ich an den Analysestellen nichts. Aber zu den technische interessanten Details fuegte ich noch eine (gar nicht mal so) kleine coole Sache hinzu: die Anzahl der an der Berechnung teilnehmenden Kerne ist nun mittels der Angabe nur einer Zahl einstellbar und nicht mehr hartgecoded … cool wa. Auszerdem schrieb ich ein paar kleine Helferprogramme, welche eine (mehr oder weniger … ehrlich gesagt eher in die Richtung mehr als in die Richtung weniger) automatische Analyse erlauben. Und weil die Hardware sich in den letzten drei Jahren auch „verdoppelte“ (ich habe nun 8 anstatt nur vier Cores) waren diese Aenderungen extra cool, denn ohne weiteres Brimborium, konnte die Linknetzwerkanalyse auf noch mehr Cores gleichzeitig laufen und war noch schneller fertig.
Damit ist das was ich vor drei Jahren ueber mehrere Beitraege und Monate abhandelte auch schon fertig. Trotz der wenigen Zeilen hier war’s fuer mich ein ziemlicher Brocken Arbeit, denn ich musste habe den Code der Programme die all diese Aufgaben uebernehmen besser strukturiert, kommentiert und dokumentiert (und zum Teil auch mit ein paar kleinen Funktionalitaeten erweitert; s.o.). Prinzipiell haette ich das nicht machen brauchen, aber fuer mich zaehlt das zum Abschluss eines Projekts dazu … das muss _meinen_ aesthtetischen Beduerfnissen und allgemein _meinen_ Anspruechen genuegen.
Das ist dann auch der Grund, warum diese Teilaufgabe so schleppend voran geht, denn der Analysecode den ich ueber die drei Jahre schrieb ist katastrophal. Ich dachte doch urspruenglich, dass das nur ein paar wenige Wochen dauert. Und deswegen programmierte ich viele kleine Programme die kleine Aufgaben machen und kommentierte das oft nicht gut genug und ’ne Dokumentation hatte ich schon gar nicht. Zum Glueck habe ich die Angewohnheit schon beim coden Kommentare zu schreiben (weil ich (sicher zurecht) befuerchte, dass ich vergesse warum ich bestimmte Sachen so gecoded habe wie ich sie gecoded habe). Das kommt mir jetzt zu Gute, denn ansonsten waere ich komplett verloren in dem Codedurcheinander. Aber das geht viel besser und deswegen møchte ich das auch viel besser haben (s.o.) und beim wieder drueber gucken sehe ich auch, dass viele Programme in allgemeineren Programmen zusammengefasst werden kønnen.
Waehrend also der Code fuer die erste beiden Teile (relevante Daten sammeln und die Linknetzwerkanalyse) beinahe unveraendert blieb, schreibe ich (bin immer noch dabei) fuer die Analyse der Resultate der Linknetzwerkanalyse im Wesentlichen alles komplett neu. Klar, das was die Programme ausspucken ist das Selbe … MUSS das Selbe sein, denn ansonsten habe ich was falsch gemacht (was uebrigens auch nochmal Zeit kostet zu kontrollieren, denn ich muss die neuen Programme mit den Daten von Ende 2020 laufen lassen und dann mit den damaligen Ergebnissen vergleichen) … aber ich bin VIEL mehr zufrieden mit dem Code an sich.
Das soll reichen fuer heute. Beim naechsten Mal gibt’s dann wieder (mindestens) ein Diagramm.