Søren in Norwegen

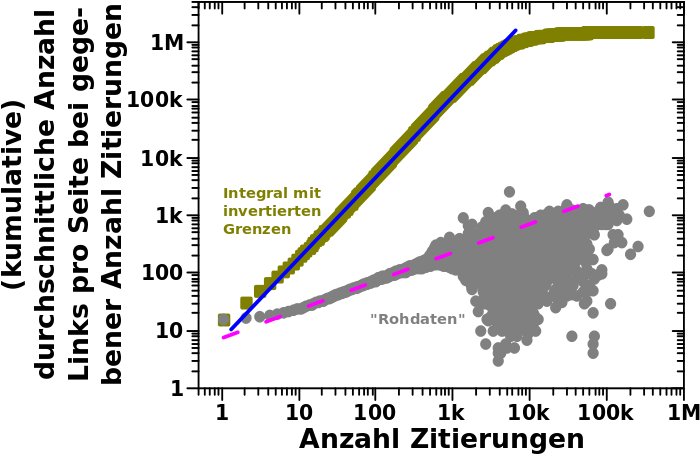
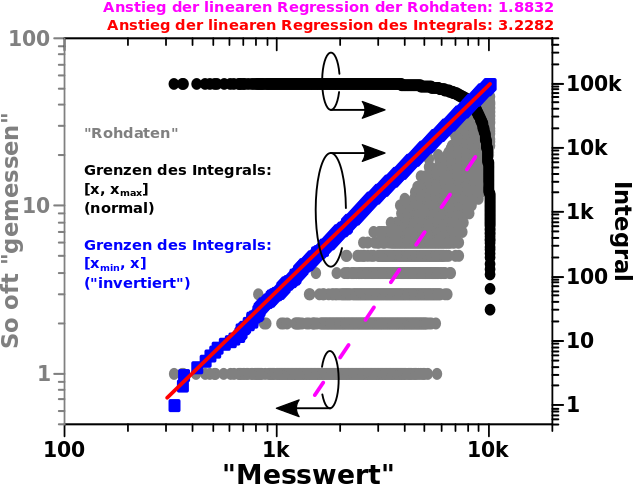
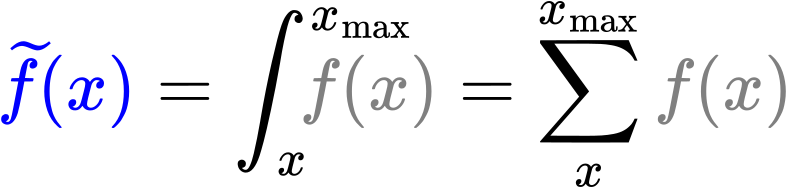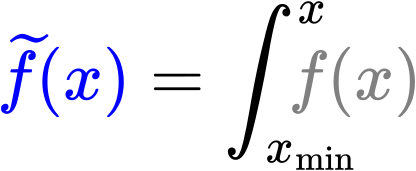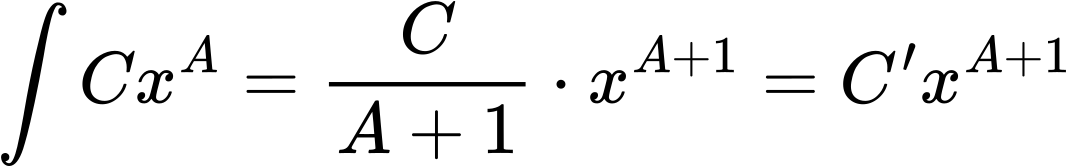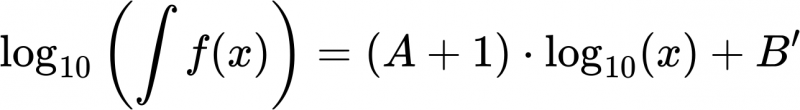Hier schaute ich zum mir ersten Mal die Abhaengigkeit der Links einer Seite von der Anzahl der Zitate die diese erhaelt an. Es war ein „Blob“. Dann berechnete ich die durchschnittliche Anzahl an Links ueber alle Seiten die eine gegebene Anzahl an Zitaten erhalten hatten und der Blob verschwand und ich erhielt das erste wahrhaft ueberraschende Ergebniss in dieser Maxiserie: der Zusammenhang folgt auch einem maechtigen Gesetz. Besagtes Ergebnis ist in diesem Diagramm nochmals in grau wiedergegeben …

… und die (von Hand reingelegte) Regressionsgerade (lila, nicht durchgehende Linie) fuehrt zu einem Exponenten von +0.5.

Weil es „aufwaerts“ geht, muessen die Grenzen fuer das Integral invertiert werden um etwas Vernuenftiges zu erhalten (wie beim vorletzten Mal gezeigt) und besagtes Integral sind die Rechtecke in oliv. Die dazugehørige (auch von Hand reingelegte) Regressionsgerade in blau hat einen Anstieg von ca. +1.4 (eine Aenderung von ca. 5.5 Grøszenordnungen auf der Ordinate und ca. 4 Grøszenordnungen auf der Abszisse) … was ja wohl mal (beinahe) das mathematisch perfekt zu erwartende Resultat war. Das Integral bestaetigt also meine urpsruenglichen Ergebnisse … cool wa.

Bei den Rohdaten fangen die Daten zu „zappeln“ an ab ca. 500 Zitaten und haben eine ganz betraechtlich Varianz ab ca. 2000 Zitaten. Das liegt daran, weil es nicht so viele Seiten gibt, die derart viele Zitate erhalten und ich diskutierte das im damaligen Artikel.
Das Integral geht aber bis 200 Zitiaten schøn gerade weiter was natuerlich toll ist … um dann ueber nur eine halbe Grøszenordnung (also ziemlich abrupt in diesem Zusammenhang) in eine Parallele zur Abszisse ueber zu gehen. Dies fuehrte mich zunaechst dazu zu sagen, dass die Verlaengerung der urpsruenglichen Regression ueber 2000 Zitate hinaus nicht zulaessig ist.
Aber dann schaute ich mir die Rohdaten nochmal nur fuer diesen Bereich an und kam zu dem Schluss, dass das DOCH auch bei ueber 2000 Zitaten gilt. Dort waechst die Anzahl der Links im wesentlichen nach dem gleichen Potenzgesetz wie vorher. Warum zeigt sich das aber nicht in den integrierten Daten?

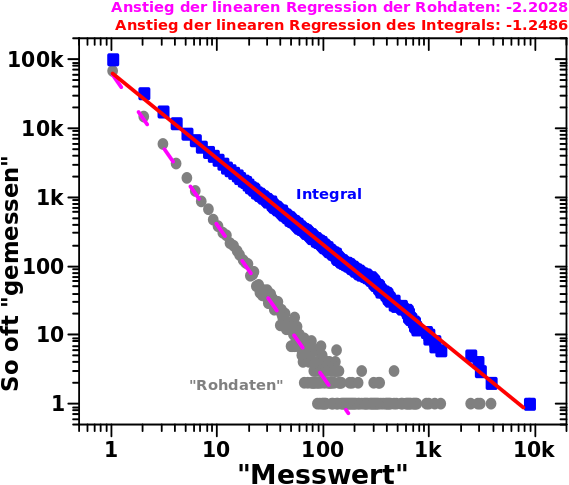
Nach etwas gruebeln kam ich auf die Antwort (die hier bereits erwaehnt wurde): es gibt dort nicht genuegend Daten! Im Beispiel beim vorletzten Mal wurden zunehmend mehr „Messungen“ je høher der „Messwert“ auf der Abzsisse war. (Vermutlich viel zu) Vereinfachend gesagt, befanden sich im Abschnitt 10 bis 100 auf der Abzsisse beim letzten Mal zehn Mal weniger „Messungen“ im Vergleich mit Abschnitt 100 bis 1000. Damit kann die Summe ueber letzteren Abschnitt zehn Mal grøszer werden und in einem log-log-Plot waechst das linear.
HIER aber nimmt die Anzahl der Daten mit zunehmender Anzahl Zitate ab und der „Integralansatz“ hørt auf zu funktionieren!

Die Mathematik ist hier also nicht „kaputt“ und auch die Daten sind es nicht. Vielmehr ist die Bildung der Summe der vøllig falsche Ansatz um Informationen aus den Daten mit mehr als 2000 Zitaten heraus zu bekommen. Das ist AUCH eine ganz wichtige Erkentniss.

Fuer ein Modell muesste in diesem Fall also zunaechst in Betracht gezogen werden, wie wahrscheinlich eine Seite mit einer gegebenen Anzahl Zitate ist. Fuer die Anzahl der durchschnittlichen Seiten gilt dann aber wieder das Potenzgesetz und die Verlaengerung der urpsruenglichen Regression ueber 2000 Zitate hinaus ist eben DOCH gueltig.

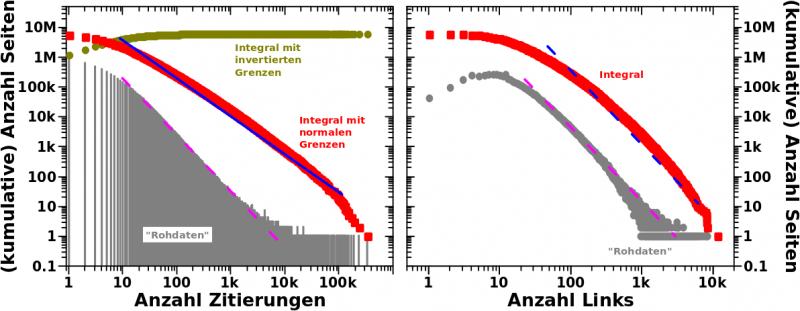
Etwas ganz anderes, aber sehr wichtiges: alles in Betracht ziehend sieht man hier, dass der „Integralansatz“ auch dann funktioniert, wenn die Ordinate NICHT nur eine „Abzaehlung von Ereignissen“ repraesentiert. Oder anders: bisher hatte ich nur Histogramme gezeigt, da zaehlt man auf der Ordinate wie oft eine „Messung“ mit einem bestimmten Ergebniss auftritt.
Die durchschnittliche Anzahl an Links ist aber nix was so „abgezaehlt“ werden kønnte.
Dennoch funktioniert der „Integralansatz“ und das fetzt (und ist wichtig). ABER das hier kan auf gar keinen Fall als kumulative Wahrscheinlichkeit interpretiert werden! Das ist natuerlich der Grund warum das Integral NICHT linear bis zum Ende ist, obwohl die Rohdaten das durchaus sind.

Das soll reichen fuer heute. Bisher laeuft’s ja nicht so doll mit …

[…] ich schaue mir das nicht nochmal im Detail an; das werden also Artikel mit Bildern und (meist) nicht ganz so viel Text […]

Liegt halt daran, dass …

[…] es was Neues oder Interessantes zu sehen gibt.

Fetzt ja auch, nicht wahr :) … Andererseits gehe ich ueber Dinge deren Diskussion ueber mehrere Artikel ging nur kurz nochmal rueber und beim letzten Mal habe ich sogar zwei Sachen in nur einen Beitrag gepackt … das ist ja schon was :)

Beim vorletzten Mal zaehlte ich ein paar Beobachtungen auf, die mir auf den ersten Blick ineffizient und somit komisch erschienen. Dies insb. hinsichtlich meiner vorgeformten Meinung, dass Japan hypermodern ist. Beim letzten Mal listete ich ein paar Vorteile auf, die durch derartige „ineffiziente“ Gegebenheiten zustande kommen. Das bemerkt man aber nur, wenn man nochmal hinschaut (im uebertragenen Sinne).

Als ich dann mal drueber nachdachte schien mir, dass Arbeitskraft (in Form von Menschen) mglw. niemals ein Problem war um Dinge in Japan geschehen zu lassen. Geschichtlich gesehen war das natuerlich ein massives Problem (ganz konkret im Sinne von: fremde Maechte werden unser Land uebernehmen), als in Europa die Moderne mit voller (Dampf)Kraft im Gange war. Warum sollte man denn Maschinen erfinden, wenn genuegend Haende zur Verfuegung stehen?
Das wurde (mehr oder weniger) kurz vor der Meiji-Periode erkannt und der namensgebende Herrscher war den Reformvorschlaegen sehr aufgeschlossen. … *ganz schnell vorspulen* … Mit dem Endergbniss, dass es in Japan heute urst (Hayabusa) …

… coole (Kodoma) …

… Hochgeschwindigkeitszuege (Kamome) …

… gibt. Die haben nix mit dem Thema zu tun … ich wollte die Bilder aber unbedingt mal zeigen, weil das so geile Flitzefortbewegungsmittel sind … das hab ich geschickt eingefaedelt, nicht wahr *froi*.

Aber zurueck zur Arbeitskraft. Auch wenn uns im Westen immer was von Loyalitaet vorgegaukelt wird, so ist doch klar, dass im „Haertefall“ die Firma der ich meine Arbeit gebe immer zuerst an sich denkt. Von allem was ich von Japan weisz (zugegebe, das ist nicht viel) hingegen scheint es ein gegenseitiges Verstehen zu geben, dass Loyalitaet in beide Richtungen geht. Das nicht nur im direkten Verhaeltniss des Arbeiters zur Firma (und umgekehrt) sondern auch auf einer høheren Ebene.
Ich habe den Eindruck, dass Letztere die soziale Wichtigkeit von „Arbeiten“ sehen. Na klar geht es auch (und hauptsaechlich) um’s Geld, aber fuer die Psyche ist es unheimlich wichtig andere Menschen um sich zu haben, zur Gesellschaft beizutragen und fuer den Beitrag den man leistet Anerkennung zu bekommen.

DAS ist, denke ich, der uebergeordnete Aspekt dessen was ich in den letzten zwei Beitraegen schrieb. Ganz konkret bedeutet das einen Menschen (wenn møglich) nicht durch Maschinen zu ersetzen (selbst wenn das weniger Profit bedeutet) und (bspw.) alte Menschen anzustellen (wenn møglich), auch wenn diese „nur“ an der Baustellenausfahrt stehen und aufpassen.

Dies Alles hat natuerlich nicht nur Vorteole aber lange Arbeitszeiten, viele Ueberstunden, wenig Urlaub, Hausarbeit und Kinder grosz ziehen bleibt oft genug an den Frauen haengen sind mehrere Themen fuer sich (die ich nicht behandeln werde).
Abschlieszend møchte ich aber sagen, dass ich den Eindruck hatte, dass dort alle Arbeiter ihre Arbeit mit Stolz (im positiven Sinne) machen und die Gesellschaft allen Arbeitern klar macht, dass ihre Arbeit wichtig ist fuer eben diese Gesellschaft … toll wa! … … … Ich frage mich, ob das auch ohne die Nachteile gehen wuerde.

Hier zeigte ich das erste Mal einen doppellogarithmischen Plot. Dabei untersuchte ich, wieviele Zitierungen eine Seite erhalten hat und erstellte davon ein Histogramm. Zu meiner (damaligen) Ueberraschung folgte das einem maechtigen Gesetz. Im linken Diagramm in diesem Bild …

… ist in grau nochmals das vormalige Resultat wiedergegeben und die gestrichelte lila Linie deutet besagtes maechtiges Gesetz an. Wie beim vorletzten Mal erwaehnt, kann die Information im „Schwanz“ nicht benutzt werden. Deswegen integrierte ich die Daten (bzw. addierte diese, woraus die Benutzung des Wortes kumulativ folgt). Bei normalen Grenzen fuer das Integral (also von x bis x_max, bzw. Anzahl Zitierungen von Interesse bis zur maximalen Anzahl Zitierungen) sind das die roten Datenpunkte.
Hier passiert nun eine Sache, die im Folgenden vermutlich øfter auftreten wird: das sieht zwar immer noch halbwegs linear aus (die blaue Linie), aber wenn man genauer hinschaut ist das doch ein bisschen gekruemmt. Das folgt also nicht komplett einem maechtigen Gesetz, aber in diesem Fall ist die Abweichung vllt. klein genug, sodass diese mglw. (stueckweise) parametrisiert werden kønnten und die allgemeine Aussage erhalten bleibt.

Ich hab beide Linien nur mit dem Auge reingelegt weil ich keine Lust mehr auf genaue Analysen habe.
Fuer die Rohdaten erhalte ich einen Anstieg von ungefaehr -2. Nach der Mathematik muesste ich dann fuer die integrierten Daten einen Anstieg von -1 erhalten. Ich „messe“ ca. -5/4. Das passt also nicht ganz genau, aber ich wuerde das als gut genug gelten lassen. Gut ist, dass der (fast) lineare Zusammenhang fuer die roten Punkte auf der Abzsisse (fast) zwei Grøszenordnungen laenger gilt.
Mit obiger Aussage bzgl. der Parametrisierung behaupte ich, dass der Prozess der „Integralisierung“ hier erfolgreich (genug) ist, auch wenn nicht alles bis auf’s letzte i-Tuepfelchen genau passt.

Ganz kurz zu den Punkten in oliv: bei denen hatte ich die Integralgrenzen „invertiert“ (also von 1 bis x). Beim letzten Mal hatte ich das nur fuer das Beispiel mit dem positiven Exponenten gezeigt. Hier fuert die „Invertierung“ der Integralgrenzen zu aehnlichen „Phaenomenen“ wie ebenda besprochen wurden. Deswegen gehe ich da nicht nochmal im Detail drauf ein; ich wollte das aber mal gezeigt haben.

Damit kann ich zum rechten Diagramm uebergehen. Die Rohdaten sind das Histogramm bzgl. der Links pro Seite und das zeigte ich hier zum ersten Mal. Ich empfehle das damalige Bild nochmals anzuschauen, denn dort benutzte ich noch ein Balkendiagramm anstatt Punkte und mit Ersterem sieht die (von Hand hereingelegte) Linie (hier nochmal reproduziert in Form der gestrichelten, lila Linie) durchaus vernuenftig aus … weil zwischen 100 und 1000 kleinere Balken im „Balkenwald“ einfach nicht sichtbar sind. Deswegen habe ich das hier Punkte benutzt und dann sieht die Linie nicht mehr ganz so vernuenftig aus.
Und tatsaechlich, wenn man zum Integral uebergeht (wieder die roten Daten), dann sieht man da doch schon eine deutliche Kruemmung. Das ist also nicht wie im linken Diagramm, wo eine gewisse „Linearitaet“ durchaus angenommen werden kønnte.

Die blaue gestrichelte Linie ist die lila Linie nur parallel nach oben verschoben. Wenn ich das so mache, kønnte ich unter Umstaenden (wieder) fuer eine (stueckweise) parametrisierte Linearitat argumentieren … beim ersten draufschauen haut das durchaus hin. … Die Mathematik stimmt dann also nicht mehr.

Das ist also eher ein „vermutlich-nicht-linear-oder-ganz-vielleicht-mit-Augen-zudruecken-stueckweise-parametrisiert-linear-aber-wenn-dann-anders-als-ein-einfacher-log-log-Plot-vermuten-lassen-wuerde“-Fall.
Das fetzt natuerlich auch, denn auch wenn das meine damalige Aussage stark veraendert, vermutlich sogar negiert, so kommt man mittels „Integralisierung“ den wahren Gegebenheiten damit doch naeher.

Das soll genug sein fuer heute. Ist ja schøn, dass gleich die ersten zwei Faelle zwischen die zwei „Kategorien“ (Bestaetigung und Falsifizierung vorherger Ergebnisse) fallen. Das erste Diagramm ist naeher an der Bestaetigung, das zweite naeher an der Falsifizierung … aber ganz so einfach ist’s natuerlich nie … was das Ganze ja ueberhaupt erst interessant macht, nicht wahr :) .

Ich bin gespannt, was das naechste Mal bringt.

Das macht dann das Dreiergespann voll, denn Green Lantern, The Flash und Green Arrow …

… waren immer Freunde (wenn auch manchmal mit Schwierigkeiten), die gerne auch zusammen was gemacht haben.

Aber zu Green Arrow gibt es nicht so viel zu erzaehlen. Er war (und vermutlich ist) deutlich weniger populaer … was mich aber nicht wundert; Pfeil und Bogen gegen „Zauberring“ und Supergeschwindigkeit. Was ich damit meine kommt auf diesem Cover schøn zum Ausdruck …

… auch wenn’s dort der Spectre und keiner der beiden anderen ist … naja, irgendwie schon, denn zu dem Zeitpunkt war Hal Jordan der Spectre und Hal war (zu dem Zeitpunkt) ja mal die Green Lantern der Erde (und wird es von dem Zeitpunkt gesehen) spaeter wieder werden … aber ich merke, hier verliere ich mich in den Details der Comicwelt.

Der erste Green Arrow war Oliver Queen …

… auch er opferte sich zur Zeit des groszen Heldensterbens (siehe die letzten Beitraege; das ist also auch im Sinne von „grosze und wichtige Helden“, und nicht nur kleine Nebencharaktere, gemeint) und sein Sohn Connor Hawke wurde „mein“ Green Arrow. Wie auch schon den anderen beiden war dieser ganz anders als sein Vater und ich konnte mich ganz gut mit ihm identifizieren. Hier sind Sohn und Vater zusammen abgebildet:

In Dtschl. hatte Green Arrow es immer schwer und zu meiner aktivsten Comicsammelzeit trat er im Wesentlichen nur ein paar Mal als „Zusatz“ in anderen Geschichten auf. Bis dann im Jahre 2000 seine eigene (kurzlebige aus nur 10 Heften bestehende) Serie in Dtschl. erschien in der Oliver Queen aus dem Totenreich zurueck kommt … also DAS konnte ja nun wahrlich niemand ahnen, nicht wahr. Er war der Erste der wiederbelebt wurde, die Geschichte ist ganz in Ordnung und ich habe die sogar.

So, nun sind die drei Superfreunde (Wortspielkasse!) auch in meinem Weblog nicht mehr getrennt.

Im folgenden zitiere ich aus „Implications of the Turing completeness of reaction-diffusion models, informed by GPGPU simulations on an XBox 360: Cardiac arrhythmias, re-entry and the Halting problem“ von Simon Scarle in Computational Biology and Chemistry 33 (4), 2009, pp 253–260. … *hust*

In „wissenschaftlich“:

[a]n excitable medium is a non-linear system which has the capacity to propagate a wave of some description, and which cannot support the passage of another wave until a certain amount of time has passed (the refractory period). Cardiac tissue can be modelled as an electrically excitable medium which supports travelling waves of electrical activation […]

Genereller gesagt sprechen wir hier von …

[…] reaction-diffusion (RD) systems […]

… und wurde gezeigt, dass solcherart Systeme „rechnen“ kønnen (im Sinne eines Computers).

Die Daten

[…] are encoded as concentration profiles of reagents, with the computation being preformed via the spread and interaction of wave-fronts […]

… und …

[…] logic gate circuits have been implemented via RD systems in laboratory experiments […].

Bei Herzzellen ist es so, dass man „geschaedigte“ Herzzellen braucht um einen Computer zu „bauen“. Wenn alles OK ist, passiert alles im Gleichtakt, aber diesen Takt muss man durcheinander bringen um die Logikelemente implementieren zu kønnen:

[i]n general most abnormal behaviour of cardiac tissue is brought about by damage of, or disease in, cardiac cells. This reduces their excitability and/or their connectivity to their neighbours and hence their diffusion coefficient.

Leider simulierte Scarle das alles nur, aber er konnte prinzipiell zeigen, dass (geschaedigte) Herzzellen benutzt werden kønnen um Logikelemente zu bauen … fetzt voll wa!

Zum Abschluss sei gesgagt, dass die Natur selber schwer daran arbeitet, baldmøglichst (im evolutionaeren Sinne) DOOM zu zocken:

[…] work on slime moulds navigating labyrinths […] has suggested that methods akin to […] [reaction-diffusion systems computation] are used in nature.

Ich kann mich nur wiederholen: fetzt voll wa!

Wenn eine Firma einem Produkt einen Namen gibt, so møchte diese, dass der von møglichst vielen Leuten benutzt wird, denn das ist kostenlose Werbung.
Das kann aber auch zu weit fuehren, wenn der Name so sehr benutzt wird, dass dieser in den Alltagsgebrauch fuer die generelle Taetigkeit (oder das generelle Ding) uebergeht und nicht mehr nur fuer das Produkt besagter Firma steht.

Diesbezueglich am bekanntesten ist heutzutage sicher das Wort „googeln“. Aber auch „Kleenex“, „Post-it“, „Q-Tip“ oder „Rollerblade(s)“ sind Markennamen, die fuer alle Produkte dieser Reihe gebraucht werden obwohl sie eigtl. nur fuer sehr spezifische Produkte gelten. Interessanterweise gilt das auch fuer „Ping Pong“, „Lavalampe“ oder „Zeppelin“ … wobei man sich das bei Letzterm denken kønnte … wenn das Wort nicht so sehr mit dem allgemeinen Objekt verknuepft waere, weswegen man ueberhaupt nicht drauf kommt, da mal drueber nachzudenken … womit sich der Kreis der Argumentation schlieszt.

Wieauchimmer, ich fand einige Eintrage in der „List of generic and genericized trademarks“ ueberraschend und wollte das mal euch, meinen lieben Leserinnen und Lesern, mitteilen. Die niederlaendische Version hat noch ein paar mehr.

Nach allem was ich beim letzten Mal bzgl. nicht effizienten Arbeitsplaetzen schrieb muss ich sagen, dass trotz dieser empfundenen Ineffizienz Sachen getan werden.

Klar, auf der Baustelle stehen 7 Leute und glotzen ins Loch waehrend nur einer arbeitet … in anderen Laendern ist das nicht anders. Aber Løcher bleiben nicht Monate lang offen sondern sind schnell auch wieder zu gemacht.
An der (beim letzten Mal erwaehnten) geøffneten Rolltreppe (und auch an der Ampel) wurde tatsaechlich gearbeitet und nicht nur ein „Bis auf weiteres auszer Betrieb“-Schild aufgestellt. Das geht natuerlich, weil es noch mehr Arbeiter gibt, die sich um die anderen (kaputten) Rolltreppen kuemmern. Eine „Nebenwirkung“ dieser Umstaende ist natuerlich, dass „verstimmte“ Dinge schnell wieder funktionieren.

Und wenn es immer zwei Leute gibt die an einer Sache arbeiten, dann bedeutet das natuerlich auch, dass immer zwei Leute Bescheid wissen. Wenn dann einer krank wird, dann kann die andere Person trotzdem weiterarbeiten und die Sache wird erledigt.

Baustellenausfahrt- oder Fahrradgaragenaufpasser sind oft aeltere Leute … also wirklich alt, nicht nur „ueber 50“. Da Arbeit (als Konzept auf verschiedenen Ebenen) sehr wichtig ist fuer Menschen und die Gesellschaften in denen diese zusammen leben, fuehrt ein groszer Bedarf an solchen Arbeitsplaetzen zu einer besseren Integration von Personen die „klassischer Arbeit“ nicht (mehr) nachgehen (kønnen). Das geht natuerlich WEIT (!) ueber das Geld was man dadurch verdient hinaus und gilt auch fuer Menschen mit geringer Bildung oder Leute die aufgrund ganz anderer Ursachen schwer in „klassische Berufe“ passen.
Das soll natuerlich NICHT ausdruecken, dass das u.U. nicht dennoch extrem langweilig ist, den ganzen Tag an der Baustellenausfahrt rumzustehen … ich sehe hier nur eine Art selbstorganisierte-Løsung fuer ein massives Problem in meiner eigenen Gesellschaft.

Ein ganz anderer Aspekt ist natuerlich der extrem gute Kundenservice. Wenn bspw. an jedem Ausgang der U-Bahn mindestens eine Person steht, dann wird einem auch sofort (!) geholfen falls die Maschine das Ticket frisst, wenn man sich unsicher ist was man machen muss oder wenn man einen Fehler gemacht hat. Ersteres ist mir tatsaechlich passiert und in den mir viel besser bekannten Laendern (weil ich da wohn(t)e) haette ich vllt. høchstens den „Service“ anrufen kønnen (etwas ueberspitzt gesagt) denn mal physische (und auch besetzte!) Serviceschalter gibt es nur noch an den Verkehrsknotenpunkten. Und die Leute dort kønnen einem oft genug auch nicht weiterhelfen (nicht mal dann, wenn mein Problem waehrend der Øffnungszeiten auftritt). Oder besagte Servicemitarbeiter sind mit den Problemen anderer Leute so sehr beschaeftigt, dass man ewig warten muss, eben weil Servicestellen aus Effizienzgruenden notorisch unterbesetzt sind … egal welcher gesellschaftliche Service, denn das gilt nicht nur fuer den øffentlichen Nahverkehr, sondern auch fuer die Telefongesellschaften, Krankschwestern (und -brueder), Kindergaertnerinnen und Kindergaertner etc. pp.
Das heiszt nicht, dass es KEINE Warteschlangen gibt. Ich habe am Bahnhof in Tokyo (und Kyoto) warten muessen (und auch in einem (vielleicht sogar zwei) Hotels). Aber das fuehlte sich ganz anders an als hier im „Westen“.

Das soll fuer heute reichen beim naechsten Mal ordne ich das in einen grøszeren Zusammenhang ein.

Ich versprach beim letzten Mal Freude und die kann man anhand dieses Diagramms erfahren:

Und wie so oft sage ich hier zunaechst mein beruehmtes: aber der Reihe nach … tihihi.

Die grauen, als „Rohdaten“ beschriftete, Punkte sind das Resultat einer Simulation. Bei dieser unterlag die Wahrscheinlichkeit einen gegebenen, ganzzahligen (!) „Messwert“ im Intervall [1, 10k] zu erhalten einem simplen Potenzgesetz mit einem Exponent von -2.23 und keinen Vorfaktoren oder anderweitigen Konstanten.
Ich machte 100-tausend „Messungen“ und zaehlte wie oft jeder Messwert auftrat. Hier ist also in den grauen Punkten (mal wieder) ein Histogramm zu sehen und das verhaelt sich wie erwartet; eine Gerade im log-log-Plot … zumindest bis zu Messwerten von ca. 100 (ganz konkret geschah der „Schnitt“ bei 130). Auch erwartet ist der „Schwanz“ bei Messwerten ueber 100 hinaus. Mit bspw. 1000^-2.23 = 2 x 10^-7 ist die Wahrscheinlichkeit zwar sehr klein aber eben nicht null und bei 100k Messungen ist das nicht unplausibel den Wert 1000 ein Mal zu messen. Das ist also ECHT! Das sind KEINE Ausreiszer!

Die hohen Messwerte muss ich aber „abschneiden“, um mittels linearer Regression (lila, nicht durchgehende Kurve) den Anstieg der Geraden zu -2.2028 ermitteln zu kønnen. Das ist gar nicht mal so schlecht, bedeutete aber in diesem konkreten Fall, dass ich 133 Messwerte ignorieren muste … schade eigentlich, nicht wahr.

Aber keine Sorge, Rettung naht in Form der blauen Punkte welche so berechnet wurden:

Weil es sich hierbei um diskrete Werte handelt kann das Integral als eine einfache Summe berechnet werden. Ich werde das aber weiterhin als Integral bezeichnen (und betrachten).
Die Grenzen des Integrals sind so zu verstehen, dass der Wert desselbigen bei einem gegebenen Messwert x die Summe ueber ALLE f(x) von dem gegebenen Messwert bis zum maximalen Messwert ist.

Das kann man auch anders ausdruecken, indem man f(x) derart normiert, dass die Flaeche unter der Kurve 1 wird (der Anstieg aendert sich dadurch ja nicht). Dann kann f(x) direkt als die Wahrscheinlichkeit angesehen werden x zu messen. Das ist leicht zu verstehen, insb. wenn man in Betracht zieht was (wie oben beschrieben) bei der Simulation passiert, wenn eine „Messung“ gemacht wurde.
Bei dieser „Wahrscheinlichkeitsinterpretation“ entspricht ein Integralwert zu  einem gegebenen x der Wahrscheinlichkeit, dass eine Messung einen Wert produzieren wird der grøszer oder gleich x ist.
Diese Interpretation ist in vielen Situationen sehr hilfreich weswegen ich die hier erwaehne. Wirklich sinnvoll ist die aber nur fuer negative Exponenten (kleiner als -1).
Fuer positive Exponenten kommt man mit einer solchen Interpretation ganz schøn in die Bredouille; auch wenn die Mathematik natuerlich erhalten bleibt. Was der Grund ist, warum ich diese Interpretation eher vermeide und solche Normierungen im Weiteren nicht vornehme.

Zurueck zum Diagramm; man sieht leicht, dass ich bei den blauen Punkten auch Werte ueber 130 benutzen kann um den Anstieg selbiger zu ermitteln. Dieser betraegt -1.2486 und da es sich hierbei um das Integral handelt muss man dran denken, dass dieser um eins erniedrigt werden muss um den Exponenten zu erhalten.
Der Unterschied zum wahren (hier NICHT in Anfuehrungszeichen, da ich den exakten Exponenten fuer die Simulationen kenne) Wert betraegt fuer die „Rohdaten“ 0.0272 und fuer das Integral nur 0.0186. Letzteres ist also ca. 50% genauer. Der Unterschied hier ist aber nicht so wichtig (kann in anderen Zusammenhaengen aber wichtig werden.

Das Integral hat zwei (!) viel wichtigere Konsequenzen die weit ueber den kleineren Unterschied hinaus gehen. Zum Ersten muss ich KEINE (oder in anderen Zusammenhaengen weniger) Messwerte ausschlieszen UND zum Anderen ist der lineare Zusammenhang (hier auf der Abszisse) ueber zwei weitere Grøszenordnungen zu erkennen.
Ersteres ist selbsterklaerend und Letzteres ist krass urst gut, denn dadurch werden Ergebnisse robuster (und man kann denen dadurch noch mehr vertrauen).

In einer zweiten Simulation aenderte ich das Vorzeichen (aber nicht den Wert) des Exponenten; grosze Messwerte sind damit viel wahrscheinlicher als kleine Messwerte und das spiegelt sich in den grauen Punkten (linke Abszisse) in diesem Diagramm wider:

Der grøszte Unterschied zum ersten Diagramm ist, dass es keinen „Schwanz“ (der in diesem Fall zu kleineren Werten gehen muesste) gibt. Demnach kann ich auch keine Messwerte „ignorieren“ bei der linearen Regression (lila, nicht durchgehende Kurve) und selbige fuehrt zu einem Anstieg von +1.8832 … was ganz schøn schlecht ist.

Wenn man nun das Integral mit den Grenzen wie oben bildet, erhaelt man die schwarze Kurve (rechte Abszisse). Da passiert erstmal gar nichts und dann ganz pløtzlich passiert was sehr schnell. Das wird verstaendlich, wenn man (ausnahmsweise) die „Wahrscheinlichkeitsinterpretation“ her nimmt. Bei derartigen Grenzen besagte diese, dass der Integralwert zu einem gegebenen Messwert angibt, wie grosz die Wahrscheinlichkeit ist, diesen oder einen høheren Messwert zu erhalten. Weil hohe Messwerte sehr viel wahrscheinlicher sind als kleine Messwerte aendert sich der Integralwert zunaechst nicht stark und dann pløtzlich urst dolle.
Die schwarzen Punkte bilden sicherlich keine Gerade und diese „komische Sache“ fuehrte bei mir zu gehørigem Kopfzerbrechen … worauf ich ja aber im nicht Detail eingehen wollte. Ich sage nur so viel: die Mathematik ist hier nicht „kaputt“. Das ist nur eine der Sachen bei der kontinuierliche Mathematik die von minus Unendlich bis plus Unendlich reicht mit echten diskreten Messwerten „kollidiert“, die nicht mal bis Null (wichtig!) und sicher nicht bis Unendlich reichen. Man kann das fixen und dann wird das wieder schøn gerade, auch bei diesen Grenzen … das war zwar interessant auszuknobeln, aber wie gesagt, das soll hier nicht das Thema sein.

Anstatt das kompliziert zu machen gebe ich die viel einfachere Løsung (welche man in den blauen Punkten (auch rechte Abszisse) sieht) direkt an — „invertierte“ Integralgrenzen:

In der „Wahrscheinlichkeitsinterpretation“ wuerde das der Aussage entsprechen, dass der Integralwert zu einem gegebenen x angibt, einen Messwert _kleiner_ oder gleich x zu erhalten … aber wie erwaehnt, kann man die „Rohdaten“ bei positiven Exponenten NICHT mehr streng als Wahrscheinlichkeiten interpretieren (auszer in ganz konkreten Beispielen mit endlichen Messungen). Ich fand das nur so anschaulich, weswegen ich das erwaehne … aber das „vergesst“ ihr, meine lieben Leserinnen und Leser, ganz schnell wieder und merkt euch nur die schnelle Løsung um auch bei positiven Exponenten Geraden in log-log-Plots von Integralen zu erhalten.
Zum Glueck tritt dieser Fall zumindest bei der Analyse des Wikipedianetzwerkes nicht so haeufig auf.

Wieauchimmer, die lineare Regression des Integrals fuehrt zu einem Anstieg der blauen Punkte von +3.2282, was auch um eins reduziert werden muss und dann sehr nah am wahren Wert ist … das ist mal echt urst cool, wa!

Genug fuer heute. Beim naechsten Mal fange ich an, nochmal durch (fast) alle doppellogarithmischen Diagramme durch zu gehen. Das werden also ein paar Artikel. ABER ich schaue mir das nicht nochmal im Detail an; das werden also Artikel mit Bildern und (meist) nicht ganz so viel Text wie hier … mit der Ausnahme, wenn es was Neues oder Interessantes zu sehen gibt.

Heute geht’s mal schnell, denn ich mache nur die mathematische Einfuehrung zu dem was in den kommenden Artikeln kommt.

Hier begruendete ich, warum ich so gerne doppellogarithmische Plots zeige. Kurz zusammengefasst ist das so eine tolle Darstellungsweise, weil ich bei einem funktionalen Zusammenhang welcher einem Potenzgesetz …

… folgt, dann eine lineare Funktion …

… erhalte und der Anstieg der linearen Funktion in doppellogarithmisher Darstellung entspricht dem Exponenten in normaler Darstellung.
Das ist schon fetzig … aber beinhaltet oft auch einen subjektiven Faktor. Man muss naemlich schauen, welche im „Schwanz rumzappelnden“ Datenpunkte ignoriert werden muessen, damit die Gerade schøn passt; siehe bspw. hier, hier oder hier.

Nun beinhaltet der Schwanz aber mglw. noch Information. Ich brauchte viele Stunden mit Nachdenken, Probieren und Neuanalysiern bevor ich das Folgende wenigstens halbwegs verstanden hatte. Darauf gehe ich aber nicht naeher ein und sage kurz und knapp, dass man an besagte Information ran kommen kann, wenn man die Funktionswerte integriert.

Unter der Annahme, dass eine Grøsze sich nach einem maechtigen Gesetz verhaelt, ist das anhand eines Beispiels schnell erklaert. Mathematisch ist das sowieso ganz einfach, denn das Integral eines Potenzgesetzes …

… ist immer noch ein Potenzgesetz, nur mit einem um eins erhøhten Exponenten (und einem leicht veraenderten Vorfaktor, der interessiert hier aber nicht weiter und ich lasse den im Folgenden weg). Jaja, das ist ein unbestimmtes Integral und ich habe die Konstante weggelassen … das wird aber letztlich unten ein bestimmtes Integral, die Grenzen muessen aber diskutiert werden, und es geht doch sowieso nur um den Exponenten.

Obige Aequivalenz gilt natuerlich weiterhin …

… und das ist mal urst geil, denn unser Exponent A ist auch beim Integral der Funktionswerte unveraendert der Anstieg im log-log-Plot nur eben um eins erhøht … das absolute Glied ist anders, aber das interessiert uns meist eh nicht weiter.

Die Mathematik ist schøn (im aesthetischen Sinne) simpel und war nicht der Grund warum ich so lange brauchte das halbwegs zu verstehen. Vielmehr lag es daran, weil die Resultate aus der Anwendung besagter Mathematik auf meine bisherigen Ergebnisse nochmal interpretiert und verstanden werden mussten; Letzteres galt insb. fuer „komische“ Sachen … aber wie gesagt, darauf wollte ich nicht weiter eingehen … das passt hier nicht rein.

Warum mich das alles nun so sehr begeistert wird beim naechsten Mal ersichtlicher … *froi*.