Ich war schon dabei zusammen zu packen, als ich ueber diese Seite (mglw. muss man nach dem klicken auf den Link die Seite nochmal refreshen um das zu sehen, was man sehen sollte) stolperte, auf der man fuer jede Wikipediaseite schauen kann, wie oft die pro Tag angeschaut wurde. Mein erster Gedanke war: das fetzt ja! Mein zweiter Gedanke war: moment Mal, damit kann ich doch direkt schauen, ob meine Annahme, dass Seiten mit mehr (Wikipedia internen) Zitaten populaerer sind, stimmt. Das konnte ich vorher naemlich nicht, weil diese Information nicht Teil des Wikipedia Quelltextes ist.
Das dortige Interface ist zwar fein, wenn man mal mit ein paar wenigen Seiten rumspielen will, aber ich wollte natuerlich die Daten fuer alle Seiten haben. Dies brachte mich (wieder) zu einer Seite, die ich bereits gaaaaanz am Anfang dieses Projekts vorstellte und dort gibt es einen Direktlink zu den Analytics data files. Von dort geht es dann weiter zu „Pageview complete“ … um dort dann mit zwei verschiedenen Rohdatenquellen konfrontiert zu werden: alte Daten und neue Daten.
Um eine etwas kompliziertere Angelegenheit kurz zu machen: es dauerte eine kleine Weile, bis ich da durchgeschaut hatte und die Datenlage ist etwas uneinheitlich und von Artefakten geplagt.
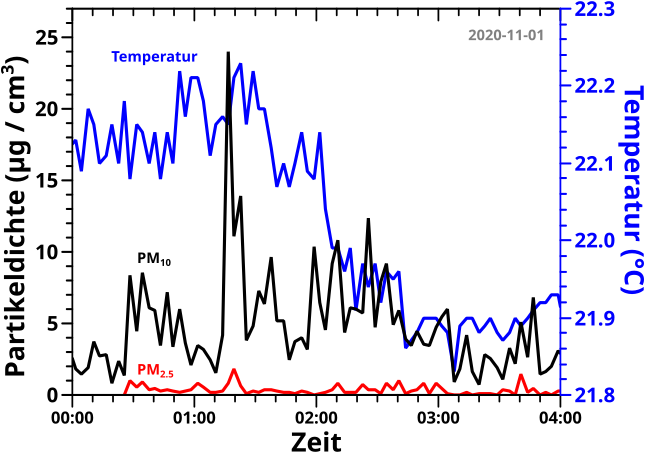
Dies hier ist ein Beispiel fuer ein unnatuerliches Artefakt (und indirekt eine Mthodenaenderung), in dem man die Klickzahlen fuer Cat und Dog fuer Juli und August 2017 sehen kann. Bei den Hunden ist alles knorke; eine im wesentlichen flach verlaufende Kurve mit ein paar Spitzen in denen ca. 2 1/2 mal so viele Leute sich fuer Hunde interessieren. Letzteres erregt mein Misstrauen erstmal nicht, denn ein Faktor von 2.5 passiert schon mal, gerne auch mehrfach. Das lohnt sich meistens nicht weiter zu untersuchen, denn vllt. gab’s da ’n Artikel ueber ’n Hund in ’ner Lokalzeitung irgendwo, oder eine Netflix-Dokumentation und solche Sachen.
Bei den Katzen hingegen sieht man einen massiven Ansteig um 1 1/2 Grøszenordnungen (!) an nur einem einzigen Tag. Es stellte sich heraus, dass Bots regelmaeszig die Wikipedia durchqueren und dann sowas verursachen. Mal mit mehr, mal mit weniger starken (aber immer deutlich herausstechenden) Klickzahlen.
Solche unnatuerlichen Peaks sind also im Wesentlichen bei allen Seiten dabei … … … bis die Wikipedia eine Methode gefunden hat die Bots zu erkennen und seitdem sind die NICHT mehr mit dabei.
Ein Beispiel fuer ein natuerliches (!) Artefakt ist der Film Tenet. Heutzutage liegt der taegliche Zaehler bei ein paar Tausend Klicks. Als der Film rauskam zeigt dieser aber bis zu ca. 50 Mal so viel an. Ist ja ganz natuerlich (insb. fuer diesen Film) und logisch, beschreibt aber nicht das normale Verhalten.
Ein weiteres Beispiel einer Methodenaenderung sind Nutzer von unterschiedlichen Hardwareplattformen. Am Anfang gab’s keine Mobilfunkversion, dann wurde das nicht unterschieden und alles nur in eine Zahl gepackt und in den neuesten Daten haben Nutzer der „mobilen Wikipedia“ ihre eigenen Klickzaehler.
Ich versuchte Artefakte in den Daten zu erkennen und „rauszurechnen“ … aber das ist alles nicht so eindeutig und fuer das was ich damit erreichen will war es mir zu viel Aufwand. Deswegen beschloss ich davon auszugehen, dass die unnatuerlichen Artefakte sich im Mittel gleich ueber alle Seiten verteilen bzw. im Groszen und Ganzen nicht weiter auffallen.
Ersteres ist durchaus eine plausible Annahme, muesste streng genommen aber nachgewiesen werden. Letzteres ergibt sich daraus, dass unnatuerliche Artefakte selten auftreten (eine weitere Annahme, die eigtl. geprueft werden muesste, aber wenn die oft auftreten wuerden, dann waeren die Statistiken prinzipiell unbrauchbar) und sich ueber’s Jahr gesehen im Mittel … øhm … herausmitteln … bzw. im „Fehler verschwinden“. Im Wesentlichen gilt das Gleiche (das Selbe?) auch fuer natuerliche Artefakte.
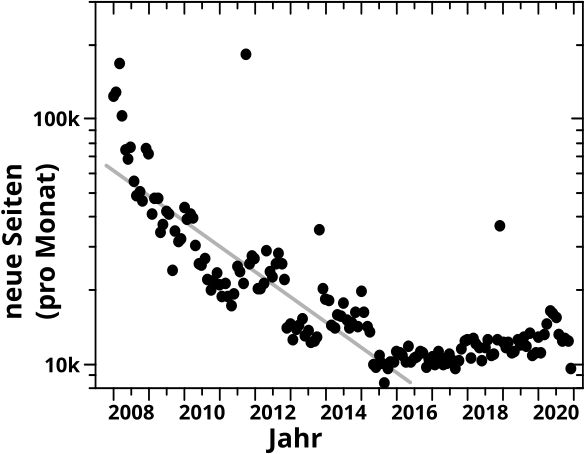
Probleme gibt es nur bei Seiten die erst seit kurzem existieren, denn da stellen potentielle (natuerliche) Artefakte einen signifikanten Anteil der Daten und hatten noch keine Zeit sich „rauszumitteln“. Andererseits habe ich ca. 6 Millionen Seiten insgesamt und pro Monat gibt’s nur … … … ja wie viele neue Seiten gibt’s denn eigentlich pro Monat?
Zum Glueck kann man das aus diesen Daten extrahieren, wenn man die zwei folgenden (wieder: durchaus plausiblen) Dinge annimmt. Eine neue Seite hat vor dem Tag ihrer „Geburt“ null Klicks. Am Erstverøffentlichungstag wird die Seite mindestens ein Mal angeklickt; naemlich vom Schøpfer selbst. Ersteres muss man nicht mal nachpruefen, denn das geht nicht anders. Bei Letzterem bin ich mir unsicher, es fuehlt sich aber richtig an; die Wikipedia ist ja nicht mein Weblog, bei dem Artikel im Voraus geschrieben um dann am Tag der Verøffentlichung nicht gelesen zu werden. Falls nicht, dann kønnte man argumentieren, dass ’ne Seite eben erst dann „wirklich geboren“ wird, wenn der erste Leser drauf klickt.
Und hier sieht man die Anzahl der neuen Seiten pro Monat seit Beginn der verfuegbaren Daten (minus ein Monat, denn als Ende 2007 die allerersten Klickzahlen registriert wurden, gab es bereits ca. 3.5 Millionen Seiten):
Die groszen Abszissenstriche kennzeichnen den Januar eines Jahres und die kleinen Abzsissenstriche liegen genau in der Mitte (also zwischen Juni und Juli). Die Jahreszahl ist auf die Mitte eines Jahres zentriert. Auszerdem habe ich natuerlich NUR die Seiten betrachtet, welche in die Kevin Bacon Analysen der letzten Jahre eingeflossen sind.
Was man im Diagramm sieht ist, dass die Anzahl neuer Seiten pro Monat _drastisch_ abgenommen hat. Die Gerade habe ich nur zum Vergleich reingelegt und bei logarithmischer Ordinate entspraeche die einem exponentiellen Abstieg … und wenn man genau hinschaut, ist das tatsaechliche Gefaelle schneller! An dem laengerfristigen Trend konnten auch die Schreibspurts (die pløtzlich auftretenden Spitzen) nur relativ kurzfristig was aendern. Bis Mitte ca. 2015 setzte sich der Trend fort und stabilisierte sich dann auf ca. zehntausend neue Seiten pro Monat, mit _ganz_ leicht steigender Tendenz (ca. 13k pro Monat Ende 2020).
Mit Blick auf Artefakte in neuen Seiten ist im Wesentlichen nur das letzte Jahr relevant. Wir reden hier also von nicht mehr als ca. 150-tausend Seiten oder ungefaehr 2.5 Prozent der ca. 6 Millionen Seiten die in meine Betrachtungen eingflossen sind. Jut … muss ich mir also keine Sorgen deswegen machen.
Das soll reichen fuer heute. Beim naechsten Mal zeig ich dann das, was ich eigtl. zeigen wollte.