Søren in Norwegen

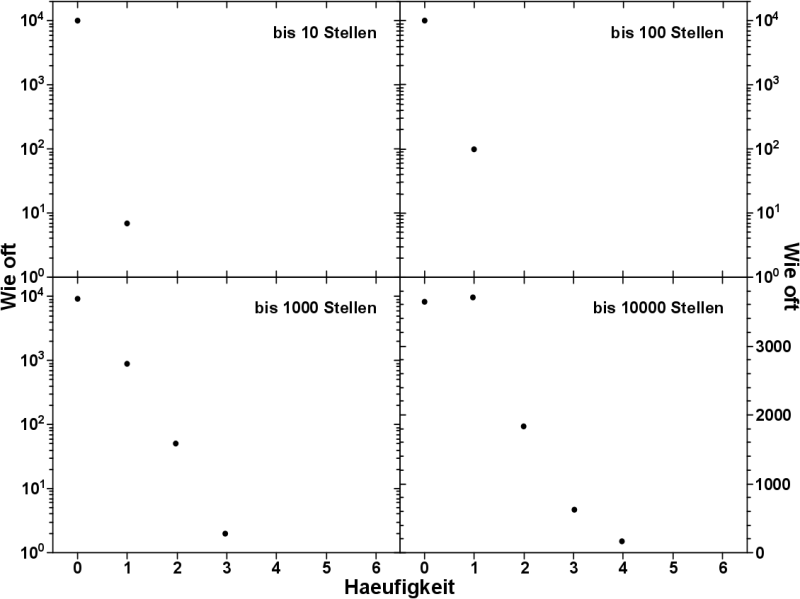
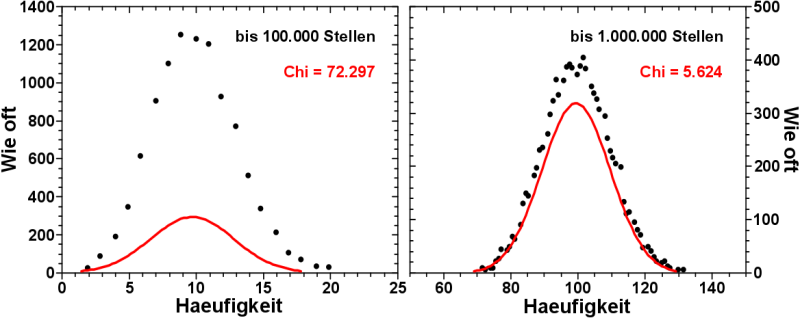
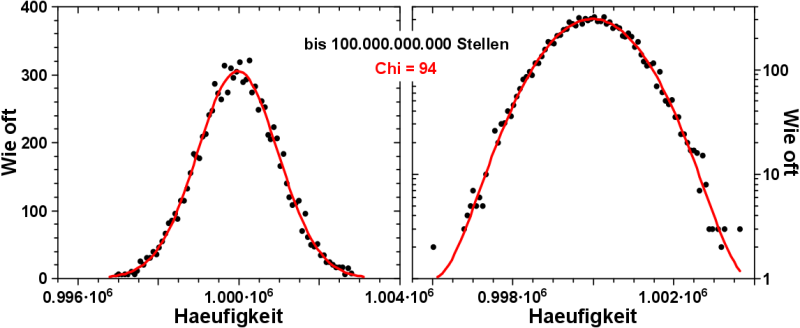
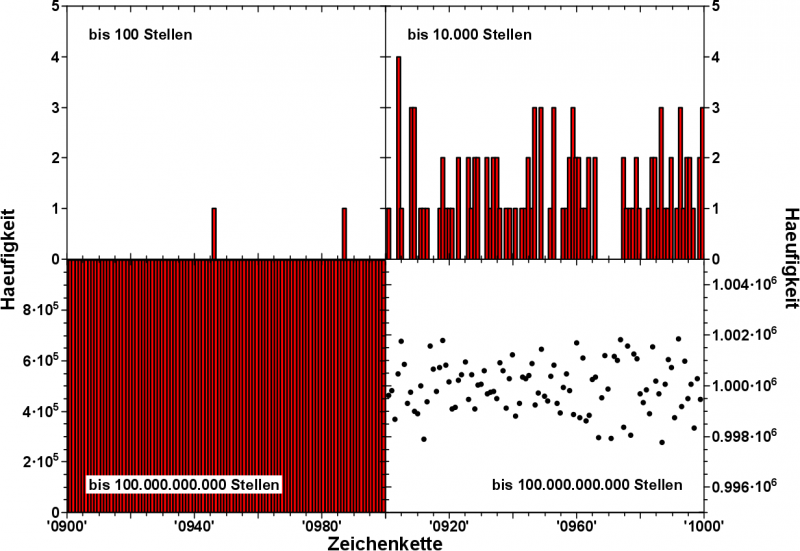
In „Science Biggest Fail“ macht Scott Adams meiner Meinung nach den Fehler, dass er wen anders (Science) beschuldigt bzgl. etwas, an dem er selber Schuld ist.

Warum ist es seine eigene Schuld, dass Sachen, die so-und-so gesagt wurden, pløtzlich ganz anders sind?

Der Gruende gibt es viele.

Der erste und wichtigste ist, dass Herr Adams erwartet, dass Science „die Wahrheit“ spricht.
Naaaaaaa? Erkennen meine lieben Leserinnen und Leser worauf ich hinaus will?
Genau: Zum Einen wurde der Prediger, welcher aus einem nicht in Frage zu stellendem Buche von der Kanzel vorliest, wurde durch den Universitaetsprofessor und Artikel in Nature, und anderen wissenschaftlichen Zeitungen, ersetzt.

Das ist Obrigkeitshørigkeit und funktioniert ganz wunderbar. Wir glauben nicht an Gott, aber an „die Wissenschaft“. Sieht manja nicht zuletzt auch an den vielen „Experten“ in den Medien.

Eine Professorin _muss_ (!) ja recht haben! (Vulgo: alles was sie spricht _muss_ ja die Wahrheit sein). Gehørt die doch schlieszlich zur „Speespitze der Intelligenz“. … Und wenn es dann auch noch in der Zeitung steht … !!!
Ein ganz hervorragendes Dogma.

Aber uh oh … Nun sagt der neue Priester Professor was ganz anderes … NEEEEEEEE! DAS geht nun wirklich nicht! Das ist nicht das woran ich geglaubt habe! Dann kann ich auch nicht mehr an Science glauben!
Und das ist auch ueberhaupt gar nicht meine eigene Schuld, dass ich vom Glauben abfalle. Ist doch gar nicht meine Verantwortung dass ich diesem Dogma folgte!

Maybe science is what needs to improve, not the citizens.

*kotz* … wobei ich ihm natuerlich recht gebe, wenn man die (im ersten Beitrag erwaehnte) „neue Definition“ von Science bedenkt.

Aber es ist natuerlich schwer (ehrlich gemeint, keine Ironie) zuzugeben, dass man bereitwillig an etwas glaubte, was wer anders gesagt hat. So musste man die vielen Artikel nicht selber lesen. So musste man nicht selber versuchen die Fehler in Studien zu erkennen. Das mache ich ja auch.

 

Zweitens macht er einen indirekten Fehler, den ich mal als „Das war doch schon immer so“ umschreibe.

Die Wissenschaft, so wie wir so romantisieren, gibt es im wesentlichen erst seit nach dem 2. Weltkrieg. Das ging zwar alles bereits um den 1. Weltkrieg los, aber wurde nicht vor dem 2. Weltkrieg so „grosz“ wie wir es heute kennen.
Und alles was es schon gab, bevor man selber bewusst in der Welt lebte, ist irgendwie „schon immer dagewesen“.

Was will ich damit sagen?

Die uns bekannten Kenntnisse, sind noch gar nicht so alt. Und wir sind im Wesentlichen immer noch dabei heraus zu finden, was funktioniert und was nicht.

Nehmen wir bspw. den Arztkittel. Weisze Reinheit. Ein Symbol fuer Sterilitaet.
Seit Jahrzehnten weisz man, dass genau das Gegenteil der Fall ist. Aerzte werden seit Jahren angehalten, ihre ganz normale (frische) Kleidung bei Krankenbesuchen zu tragen, weil die weniger Keime transportiert, als Arztkittel. Aber diese Erkenntnis setzt sich erst langsam durch. Warum?
Bis ca. in die 50’er/60/er Jahre waren die allgemeinen hygienischen Verhaeltnisse derart schlecht, dass der Arztkittel tatsaechlich besser war als Alltagskleidung. Als Stichwort sei hier auf Ignaz Semmelweis verwiesen. Dann wurde dieses allgemeine Problem aber schrittweise geløst und der Arztkittel wurde ein Problem.

Wir haben also etwas, was bald ein Jahrhundert „wahr“ war. Alle haben das gelernt. Dann trifft es aber nicht mehr zu. Aber wir haben es doch so gelernt. Es ist schwer, vom Glauben abzukommen. Das war doch schon immer so.

Da muss die naechste Generation ran und das aendern. Die werden aber von uns „Altglaeubigen“ unterrichtet. Da schleift sich die alte Erkenntnis also noch ein bisschen mit, bevor es dann ausgemerzt ist.

Oder bis der Arztkittel dann in einen richtigen Kontext einsortiert ist.

Bzgl. Sterilitaet und Reinheit gibt es noch so ein Ding. Es wurde gelernt, dass das wichtig ist, um Krankheiten nicht zu verbreiten. Forschung zeigt aber, dass aber mglw. durch zu wenige „Keime“ die Entstehung von Allergien beguenstigt werden.

Aber ich kenne mich da nicht aus.

Oder nehmen wir doch das „Schuhe in der Wohnung ausziehen“. Dies macht man um keinen Dreck in die Whg. zu tragen. Aber an einem normalen Tag, sind unsere Schuhe dreckiger als die Pantoffeln, die wir jahrelang auch in der Kueche tragen, wo ja doch ab und zu mal was runterfaellt, ohne, dass man es bemerkt? Ist da Kuhmist dran? Oder Schlamm, weil die Strasze nicht betoniert ist?
Ich rede nicht von Regenwetterschuhen, aber der Partybesuch kønnte an einem Sommertag doch auch mal die Schuhe anlassen, nicht wahr? Die Chipskruemel nach dem Feste sind mehr Dreck, als das bisschen Sand.

Der Punkt des Ganzen soll sein: Wir arbeiten mit Erkenntnissen, die lange richtig waren. Wir haben die lieb gewonnen.
Neue Erkenntnisse brauchen aber eine Weile, bevor sie von der Allgemeinheit akzeptiert werden.
Das ist dann aber kein Fehler von Science, sondern das ist einfach so.

Und nochmal zurueck zu“erst nach dem 2. Weltkrieg“.

Vorher waren die Erkenntnisse und damit geløsten Probleme „grosz“ und allgegenwaertig (Hygiene bspw.) und konnten durch einfache Masznahmen angegangen werden. Das brauchte dann natuerlich nicht viel Forschung um die Zusammenhaenge zu erkennen und einen nachhaltigen Einfluss zu haben.

Vieles ist aber deutlich komplexer als es erstmal scheint. Das braucht dann aber viel Forschung und viel Geld und viel Zeit um es zu verstehen.
Das dauert eine Weile das alles zusammen zu bekommen.

Und wenn das dann noch gegen das ist, was vorher so erfolgreich war, dann muss man auch noch die „etablierten Helden“ vom „Throne“ holen.

Also: wir arbeiten mit alten Erkenntnissen und es ist ein Zeichen der Staerke der Wissenschaft, dass diese in Frage gestellt werden und auch etwas vøllig neues die Lehrmeinung wird!

Ist natuerlich scheisze, wenn das die eigenen alten Dogmen sind, die pløtzlich nicht mehr gelten.

Aber hey! Das ist dann nicht die Schuld der Religion, dass ich da bisher dran geglaubt hat, denn die Prediger erzaehlen ja auch nur das, woran sie selbst glauben und im Falle der Wissenschaft ist es eben das, was dem aktuellen Stand der Forschung entspricht.

 

Ach Scheiszdreck! Alles so kompliziert.

In kurz: Scott Adams (und nicht nur der) hat an das geglaubt, was andere Leute ihm erzaehlt haben. Nun erzaehlen diese anderen Leute was anderes. Das passt aber irgendwie nicht zu dem vorher Gesagten. Jetzt betrachtet er auch nicht, wie das (alte und neue) Gesagte eigentlich entstanden ist. Wie das alte Gesagte durchaus richtig war, aber jetzt durch etwas Besseres ersetzt wurde.
Nein! Das passt nicht und deswegen wird alles in Frage gestellt.
Anstatt seine eigene Herangehensweise an die Sache in Frage zu stellen.
Oder anders: selber lesen macht schlau!

Nicht ins Detail gehen (aber ich møchte es nicht unerwaehnt lassen) kann ich jetzt bezueglich der Rolle der Medien, oder die wissenschaftliche Methode. Denn Scott Adams regt sich auf ueber etwas, was charakteristisch fuer Letztere ist: Wir stellen Hypothesen auf und testen diese so lange, bis sie falsifizieren sind, denn beweisen kønnen wir die nicht. Wenn wir die aber nicht beweisen kønnen, kønnen sie auch nie als „die absolute, fuer immer und ewig geltende Wahrheit“ fungieren. Und das vergisst er.

Oder anders: Newton ist nicht falsch! Nur ist das Ganze deutlich komplizierter, wenn man mal drueber nachdenkt.

Oder noch anders: Wie jede Religion taugt auch Science nicht als Ersatz fuers selber nachdenken!

Eigentlich interessiert mich ja nicht die Haeufigkeit einer bestimmten Zeichenkette. Wirklich von Interesse ist die Streuung der Haeufigkeiten der Zeichenketten.
Oder einfacher (aber mit mehr Worten) erklaert: wenn bspw. die Zeichenkette „1234“ fuenf Mal vor kommt, so møchte ich wissen, wie viele Zeichenkette auch fuenf mal vorkomen. Dabei interessiert es mich nicht die Bohne, welche Zeichenketten das sind.
Bestimmte Zahlen weisen eine gewisse Haeufigkeit auf und mich interessiert es, wie oft diese Haeufigkeit auftritt. Hier vermute ich die Normalverteilung.

Aber schauen wir uns doch konkrete Daten, fuer vierstellige Zeichenketten, an:

So lange die Anzahl der Stellen in der Folge nicht ausreicht, damit jede Zahl mehr als ein Mal auftreten kønnte, ist natuerlich keine glockenførmige Verteilung zu erkennen. Dies sieht man in diesen vier Grafen.

Wenn die Folge nur 10 Zeichen lang ist, so kommen ca. 10.000 vierstellige Zeichenketten genau null Mal vor. Und ein paar wenige ein Mal.
Je laenger die Folge wird, desto mehr Zeichenketten kønnen ein Mal vorkommen (bis 100 Stellen) und irgendwann auch øfter als ein Mal (bis 1000 Stellen). Allerdings nimmt das Vorkommen høherer Haeufigkeiten exponentiell ab. Was zu erwarten war.

Ab einer Folgenlaenge von 10.000 Zeichen, kommt im Schnitt jedes Zeichen genau ein Mal vor. Das hatte ich ja bereits letztes Mal gezeigt.
Man beachte, dass die Ordinate nun linear ist!

Und wenn die Folge weiter waechst, so stellt sich auch eine glockenførmige Verteilung ein:

Aber HAEH?! Wieso liegt denn die schicke rote Kurve (vulgo: der Fit) nicht auf den Datenpunkten? Und was ist dieses komische „Chi“?

Dies liegt daran, weil diese schøne rote Kurve den Daten angepasst wurde, unter der Annahme, dass diese normalverteilt sind. Und hier kommt Chi ins Spiel. Chi ist ein Ausdruck fuer die Guete des Fits. Je høher dieser Wert, desto schlechter stimmen die Daten mit der Annahme ueberein.
Oder andersherum: das Datenauswertungsprogramm passt die Parameter der Kurve derart an, dass Chi so gering wie møglich wird. Nicht, dass es am Schønsten aus sieht.

Demnach kønnte man sagen, dass bis zu einer Folgenlaenge von 100.000 Stellen fuer vierstellige Zeichenketten NICHT normalverteilt ist.

Aber wie das rechte Bild zeigt, so scheint sich sich die Verteilung einer Normalverteilung anzunaehern, mit zunehmender Folgenlaenge.

Und hier nun, ENDLICH, kommt das, worauf ihr, meine lieben Leserinnen und Leser, so lange warten musstet:

Bei einer Fibonaccifolgenlaenge von 100.000.000.000 Stellen, meine ich, dass man durchaus davon sprechen kann, dass vierstellige Zeichenketten normalverteilt sind. Toll wa!

Dies gilt insb. auch fuer kleine Vorkommen, was die logarithmische Darstellung im rechten Bild eindrucksvoll zeigt.

Damit hatte ich endlich herausgefunden, was ich herausfinden wollte. Natuerlich nur innerhalb meines eigenen, mathematisch nicht so anspruchsvollen Rahmens.
Und ihr, meine lieben Leser und Leserinnen, wisst es nun auch.

Nun rechnete und rechnete mein kleiner braver Laptop 15 Stunden ohne Unterbrechung und heraus kamen viele Zahlen.

Es werden nur noch die Daten fuer vierstellige Zeichenfolgen betrachtet.
Drei-, zwei- und einstellige Zeichenfolgen passen in das Modell gut rein, es sieht aber nicht so schøn aus. Also vom aesthetischen Anspruch mein ich.
Dies, weil sich bei nur 1.000, 100 bzw. 10 Datenpunkten statistische Schwankungen noch deutlich negativ auf das Erscheinungsbild auswirken kønnen, selbst wenn diese einer Normalverteilung folgen und mathematisch somit alles in Ordnung ist. Bei 4-stelligen Zeichenketten habe ich aber 10.000 Datenpunkte und die Schwankungen folgen einer schønen Glocke. Aber so weit sind wir ja noch gar nicht.

Wie sieht denn nun so eine Verteilung von 4-stelligen Zeichenketten aus. Im folgenden Bild stelle ich dies beispielhaft dar, fuer Fibonaccifolgenlaengen von 100, 10.000 und 10¹⁰ Zeichen.

Hier gezeigt ist die Entwicklung der Haeufigkeiten der Zeichenketten von „0900“ bis „1000“.

Bei einer Fibonaccifolgenlaenge von nur 100 Zeichen, kommen auch nur ca. 100 vierstellige Zeichenketten vor. Also im Durchschnitt kommt jede von den 10.000 vierstelligen Zeichenketten 0.01 mal vor. Dies zeigt die linke obere Verteilung sehr deutlich.

Bei einer Fibonaccifolgenlaenge von 10.000 Zeichen, kommt jede vierstellige Zeichenkette im Schnitt genau ein Mal vor. Dies bestaetigt die rechte obere Verteilung.
Hier spielt uns die menschliche Wahrnehmung aber einen Streich. Es scheint, als ob Haeufigkeiten von 2, 3 und gar 4, mal deutlich die Zahl der „Nullvorkommen“ ueberwiegen. Dem ist aber nicht so. Manuelles Nachzaehlen ergab, dass alle Haeufigkeiten die ueber eins liegen, die „Leerstellen“ ziemlich genau „auffuellen“, so dass im Durchschnitt eine Haeufigkeit von eins heraus kommt. So wie erwartet.

Bei einer Fibonaccifolgenlaenge von 10¹⁰ Zeichen ist die Erwartung, dass jede vierstellige Zeichenkette durchschnittlich eine Million mal auftritt. Dies sieht man in der linken unteren Verteilung bestaetigt. Im Balkendiagramm von 0 bis 1.000.000 gehen die Feinheiten aber unter. Deswegen ist unten rechts der Bereich der Verteilung um den Wert „1.000.000“ aufgespreizt zu sehen.

Und hier beginnt es interessant zu werden.

Dieses Zappeln um den Mittelwert ist ja das eigentliche Ziel meiner Fragestellung. Ist das normalverteilt?
Wie haeufig eine bestimmte Zahlenfolge vorkommt, ist also ueberhaupt nicht von Interesse. Aber wie sich die Haeufigkeit eben dieser Zahlenfolge von den Haeufigkeiten aller anderen Zahlenfolgen unterscheidet, DAS ist das Interessante. … Das Zappeln um den Mittelwert halt.

Ich kønnte hier gleich das Ergebnis praesentieren. Das waere aber langweilig.
Zunaechst einmal schauen wir uns das Zappeln und die Entwicklung des Zappelns ein bisschen naeher an.

Zur Analyse ist es unpraktisch, sich die Rohdaten anzuschauen. Da erhaelt man keine wesentlichen Informationen, denn ich habe ja prinzipiell 10.000 verschiedene Haeufigkeiten. Nun ist meine Vermutung aber, dass es deutlich wahrscheinlicher ist, dass das Vorkommen einer Zeichenkette um den Mittelwert liegt, als fern ab davon. Um dies besser zu „sehen“, erstellte ich fuer jede Potenz der Fibonaccifolgenlaenge ein Histogramm der Haeufigkeiten vierstelliger Zeichenketten. Bei diesen Histogrammen „mittelte“ ich derart, dass ich 100, gleich weite Balken hatte. Dieses Histogramm sollte dann natuerlich einer Normalverteilug entsprechen. Dazu aber an anderer Stelle mehr.

Es gibt die folgenden interessanten Grøszen:
– maximales und minimales Vorkommen;
– die Differenz daraus ergibt die Fehlerspanne;
– „DeltaMinus“ und „DeltaPlus“, der maximale Betrag der Abweichung vom Vorkommensmittelwert nach unten bzw. nach oben;
– eine Groesze die ich „relativer Fehler“ nenne: Quotient aus Fehlerspanne und Mittelwert.

Dies alles natuerlich in Abhaengigkeit von der Laenge der Fibonaccifolge.

Maximales und minimales Vorkommen sind nur in so fern von Interesse weil sich daraus andere Daten ergeben.

„Delta Minus“ und „Delta Plus“ haben eigentlich keine Bedeutung. Aber ich wollte gern mal wissen, ob die Abweichung nach oben tendentiell grøszer ist, als die nach unten (oder umgekehrt).

Bis zu einer Fibonaccifolgelaenge von 10.000 Stellen war das minimale Vorkommen immer null. Natuerlich gab es Zeichenketten, die ueberhaupt nicht aufgetaucht sind, wenn es nur so wenige potentielle Zeichenketten ueberhaupt gab.
Das maximale/minimale Vorkommen nimmt, wie zu erwarten war, exponentiell  zu, nachdem die Fibonaccifolge eine Mindestlaenge von 10.000 Zeichen ueberrschritten hat.

Der Betrag des maximalen Abstands vom Vorkommensmittelwert nach unten (DeltaMinus, rote Punkte im unteren Grafen) ist zunaechst immer grøszer als der Abstand nach oben (DeltaPlus, schwarze Punkte im unteren Grafen). Erst im ganz letzten Messwert kommt es zu einem Umschlag dieses Verhaltens. Erwarten wuerde ich, dass es hierbei keine Praeferenz gibt. So weit scheinen die Daten allerdings Letzteres zu suggerieren. Mehr Daten sind vonnøten und ein strenger mathematischer Beweis dieser Behauptung.

Die Fehlerspanne nimmt exponentiell zu. Der Abstand zwischen der Zeichenkette die am seltensten vorkommt und derjenigen, die am haeufigsten vorkommt, wird also absolut gesehen immer grøszer.
Auch dies ist so zu erwarten gewesen, kann sich das Vorkommen aller Zeichenketten bei laengeren Fibonaccifolgen doch ueber grøszere Bereiche „ausdehnen“.

Deswegen fuehre ich den „relativen Fehler“ ein. Auch wenn die Fehlerspanne immer grøszer wird, so wuerde ich erwarten, dass diese Fehlerspanne bezogen auf den Mittelwert des Vorkommens aller Zahlen abnehmen sollte. Die Haeufigkeiten sollten sich also relativ gesehen mehr und mehr an den Erwartungswert „anschmiegen“.
Diese Vermutung kommt _mir_ total natuerlich vor, weil ich eine Normalverteilung aller Zeichenketten annehme. Wenn ich aber mal so drueber nachdenke, dann beruht diese Annahme nur auf so ’nem „Bauchgefuehl“. Und wenn ich so weiter drueber nachdenke, dann werde ich mir unsicher, ob nicht selbst bei einer Normalverteilung der Werte, der relative Fehler immer grøszer werden kønnte … wenn also die Fehlerspanne schneller zu nimmt, als der Mittelwert grøszer wird … nein … mich duenkt, bei einer Normalverteilung kann dem nicht so sein. Aber eine Begruendung muss ich schuldig bleiben. Jedenfalls ist fest zu halten, im Allgemeinen kønnte der relative Fehler auch gleich bleiben, oder sogar zu nehmen. Wenn dem aber so waere, dann waere vermutlich die Annahme einer Normalverteilung falsch.
Jedenfalls ist in der Abbildung gut zu erkennen, dass meine Vermutung richtig war und im Umkehrschluss mglw. auch die Annahme der Normalverteilung. Dazu aber nicht mehr in diesem Beitrag. Auf dieses wunderschøne Ergebniss muesst ihr, meine lieben Leserinnen und Leser, euch bis zum naechsten Mal gedulden.

Zum Abschluss des Beitrages noch das Folgende.
ACHTUNG! Die Definition „_meines_ relativen Fehlers“ hat nichts mit dem relativen Fehler zu tun, wie er vom Studium und aus der Mathematik her bekannt sein sollte. Dieser wird naemlich bspw. fuer einzelne Messwerte angegeben, als (relative) Abweichung vom wahren Wert. Hier habe ich aber ein Ensemble von Messwerten und betrachte die Gesamtheit.

Bevor ich meinen Rechner viele Stunden rechnen lassen wollte, schaute ich mir erstmal an, wie sich die Rechenzeit in Abhaengigkeit von den Parametern verhaelt.
Wir (also ihr, meine lieben Leserinnen und Leser, zusammen mit mir) erinnern uns: die Laenge bis zu der die Fibonaccifolge ausgerechnet und untersucht werden soll ist einer der Parameter und die Laenge der Zeichenketten die untersucht werden sollen die andere.
Bei Letzterem ist zu beachten, dass ich immer alle Zeichenketten BIS zu der maximalen Laenge untersucht habe. Wenn vierstellige Zeichenketten von Interesse sind, wurden also auch alle drei-, zwei- und einstelligen Zeichenketten mit untersucht.
Warum Daten nicht benutzen, die ohnehin mit anfallen? … jajaja … Das Programm haette ich auch anders schreiben kønnen, sodass die nicht anfallen. Aber da ich zu dem Zeitpunkt noch nicht wusste, was ich an Daten brauche, habe ich alles „aufgesaugt“ was geht. Sozusagen wie google und facebook und die nsa und der sog. Verfassungs“schutz“ usw. usf. … ihr, meine lieben Leser und Leserinnen, versteht sicherlich, worauf ich hinaus will.

Aber ich schwoff ab.

Die Rechenzeit in Abhaengigkeit von der Gesamtlaenge der Folge und von der Laenge der zu untersuchenden Zeichenkette schaute ich mir in einer weniger lang dauernden Voruntersuchung an. Bei dieser Voruntersuchung rechnete der Rechner nur ca. 1 1/2 Stunden. Ich extrapolierte dann die Daten um festzulegen, bis zu welcher Zeichenkettenlaenge ich, in der laenger dauernden Untersuchung, die Fibonaccifolge analysieren møchte und wie lang diese werden soll.

Bei dieser Voruntersuchung kam es zu einigen Resultaten, mit denen ich, gelinde gesagt, nicht gerechnet hatte und die mir so einiges Kopfzerbrechen bereiteten.

Aber hier nun die schønen Grafiken. Zunaechst die Rechenzeit in Abhaengigkeit von der Laenge der Folge; die Abhaengigkeit von der Laenge der zu untersuchenden (laengsten) Zeichenkette ist durch verschiedenfarbige Datenpunkte angedeutet.

Erwartet haette ich, dass mit jeder hinzukommenden Potenz der Reihe, also mit jeder Erhøhung der Anzahl der Zeichen in der Folge um den Faktor 10, die Rechenzeit auch um den Faktor 10 zu nimmt. Wenn ich 10 Millionen Zahlen erstellen und untersuchen muss anstatt nur 1 Million, so ist diese Annahme durchaus plausibel.

Wenn ich nur Zeichenketten mit bis zwei Zeichen untersuche (schwarze Punkte), so stimmt das Ergebis gut mit dieser Annahme ueberein.
Es kommt zu Abweichungen bei kuerzeren Folgenlaengen, aber man beachte diesbezueglich die logarithmische Darstellung. Ob der Rechner drei Hundertstelsekunden rechnet, oder nur eine Hundertstelsekunde ist im Ganzen kein groszer Unterschied, macht sich aber bei dieser Darstellung ueberdeutlich bemerkbar.
Die hell-lila Gerade durch diese Datenpunkte zeigt doch eindruecklich, dass die Annahme plausibel ist.

Die erste Ueberraschung war, dass sich bei laengeren zu untersuchenden Zeichenketten (blaue und rote Vierecke), die Rechenzeit fuer kuerze Folgenlaengen zunaechst linear entwickelt (dunkel-lila Geraden), bevor sie denn in das erwartete exponentielle Verhalten uebergeht.
Nun ja, wie sagte einer meiner ehemaligen Professoren es mal so schøn: wer bei doppellogarithmischer Darstellung keine Gerade durch die Datenpunkte legen kann, muss schon ziemlich blød sein. Eine Gerade mit flacherem Anstieg muss also nicht unbedingt bedeuten, dass es sich auch im lineares Verhalten handelt.

Deswegen trug ich die Abhaengigkeit der Rechenzeit von der Laenge der Folge linear (!) auf, nur fuer den Datensatz zur Analyse von siebenstelligen (und kuerzeren) Zeichenketten (rechte Grafik). Eine Gerade in dieser Darstellung bedeutet dann natuerlich, dass sich die Rechenzeit tatsaechlich zunaechst linearar entwickelt.

Hierbei ist zu beachten, dass nicht die eigentliche Laenge der Folge von Interesse ist. Also schon, aber nur in „Schritten“ von Zehnerpotenzen. Genauer gesagt verhaelt sich also die Rechenzeit linear in Abhangigkeit von der Potenz der Laenge der Folge.

Wie ist dieses unerwartete Verhalten aber nun zu erklaeren? Ich schlage folgendes vor und hoffe, dass mich Experten, die sich besser mit Speicherzugriff usw. auskennen, berichtigen (oder bestaetigen).

Nehmen wir eine Laenge der Folge von 1 Millionen Zeichen (10⁶) an. Dann gibt es in dieser Folge auch 1 Millionen „Zahlen“ die 7 Stellen lang sind. Es gibt aber 10 Millionen (!) unterschiedliche Zeichenketten, die 7 Stellen lang sind. Alles von „0.000.000“ bis „9.999.999“ (ohne die Punkte natuerlich). Ich sehe also nur 10% aller 7-stelligen Zeichenketten. So lange wie die Folge so kurz ist, muss ich also nur auf 10% des Speichers fuer 7-stellige Zeichenketten zugreifen. Bzw. nur 10% aller 7-stelligen Zahlen ueberhaupt analysieren (im Sinne von umwandeln eines Strings in eine Zahl und dann diese Zahl erkennen und deren Vorkommen um eins erhøhen). Erst bei der naechsten Potenz der Folge (wenn ich also 10 Millionen Zeichen untersuche) wird die Analyse- und Speicherzugriffszeit relevant. Vorher ist der Anstieg der Rechenzeit also deswegen deutlich geringer, weil auf nicht so viele Speicherzellen zugegriffen und weil nicht so viel analysiert werden muss.
Gerade beim letzten Teil der Erklaerung bin ich unsicher und hoffe wirklich, dass sich da eine Expertin oder ein Experte unter meinen Lesern befindet.

Hierbei ist das zu bedenken, was ich bereits im zweiten Artikel dieser Reihe ansprach. Die „Groesze“ der Tabelle der Haeufigkeiten der untersuchten Zeichenketten wird (fast) nur durch die Laenge der laengsten zu untersuchenden Zeichenkette bestimmt.

 

 

Nun kommt die Abhaengigkeit der Rechenzeit von der Laenge der zu untersuchenden Zeichenketten, fuer eine gegebene Laenge der Folge.

Hier ist das Resultat:

Erwartet haette ich hier, dass sich mit jeder Stelle die die zu untersuchende Zeichenkette laenger wird, die Rechenzeit linear zu nimmt.
Warum diese Annahme? Der bereits mehrfach beschriebene Analysealgorithmus – extrahiere Zeichenketten mit der maximalen Laenge, analysiere diese, schneide von dieser Zeichenkette ein Zeichen ab, analysiere diese neue, kuerze Zeichenkette usw. – ist mit einer einfachen Schleife zu realisieren.
Nehmen wir an, einstellige Zeichenketten sollen untersucht werden. Die Analyse einer einstelligen Zeichenkette dauert dann eine Zeiteinheit. Nehme ich jetzt zweistellige Zeichenketten, so dauert die Analyse zwei Zeiteinheiten. Die Zeit, die es braucht um die zweistellige Zeichenkette zu erfassen und den Zaehler um eins zu erhøhen und die bereits vorher auch benøtigte Zeit, um die einstellige Zeichenkette zu analysieren. Bei dreistelligen Zeichenketten kommt wiederum nur eine einzige Zeiteinheit hinzu.

Im rechten Bild (Achtung: lineare Skala!) sieht man diese Annahme bestaetigt. Ist die Fibonaccifolge sehr lang, nimmt die Rechenzeit linear mit der Laenge der zu untersuchenden Zeichenkette zu.

Im linken Bild (doppellogarithmische Skala!) hingegen sieht man, dass man im Wesentlichen das umgekehrte Verhalten zur vorherigen Problemstellung hatte. Kurioserweise ist das qualitative Resultat das Gleiche.
Ist die Laenge der Fibonaccifolge kurz (100 Zeichen, schwarze Punkte), so nimmt die Rechenzeit exponentiell (und nicht linear) zu mit jedem Zeichen, dass die zu untersuchende Zeichenkette laenger wird.
Wird die Folge laenger, so ist die Abhaengigkeit zunaechst linear, bis sie dann bei laengeren Zeichenketten zu exponentiellen Verhalten umschlaegt.

Darueber musste ich etwas laenger nachdenken. Hier ist eine møgliche Erklaerung.

Wenn in der zu untersuchenden Zeichenkette eine Stelle dazu kommt, dann muss 10 mal mehr Speicher “durchgerødelt” werden. Die oben erwaehnte Haeufigkeitstabelle. Auch wenn letztlich bei jedem Durchgang durch die Analyseschleife nur in eine Zeile in der Tabelle geschrieben werden muss, so muss der „Schreibstift“ (oder Schreibkopf oder Zaehler, oder vermutlich viel mehr programminterne Speicherzugriffsalgorithmen) erstmal immer bis zu dem Platz in der Tabelle „laufen“. 10 mal mehr Speicher „durchrødeln“ bedeutet exponentielles Verhalten.
Das Problem dabei ist, dass das auch bei langen Folgen der Fall waere. Ich wuerde also auch dort kein lineares Verhalten sehen, was ja aber der Fall ist.
Dies konnte ich mir nur dadurch erklaeren, dass dieser Effekt (das „Laufen“ des „Schreibstiftes“ an die Stelle zum schreiben) zwar vorhanden, aber absolut gesehen relativ klein ist. Der „Schreibstift“ ist sozusagen ein schneller „Laeufer“. An den Datenpunkten sieht man, dass dieser bspw. nur 20 Sekunden braucht, um bei einer 100-stelligen Folge, mehrfach durch die gesamte Tabelle fuer 7-stellige Zeichenketten  zu gehen.
Ist die Fibonaccifolge nun kurz, so dauern die eigentlichen („Abschneide-“ und) Analyseschritte aber ebenso nicht so lange, sodass dieser Effekt signifikant wird.
Bei einer langen Folgen hingegen, dauern die eigentlichen Analyseschritte so lange (bspw. 1.000 Sekunden), sodass das „durchrødeln“ durch die Tabelle (der „Lauf zur richtigen Spalte“) NACH der eigentlichen Analyse nur noch ein paar Prozent an der der gesamten Zeit aus macht. 20 Sekunden (ja sogar 200 Sekunden) sind nicht so relevant bei 1000 Sekunden Gesamtrechenzeit.
Dummerweise habe ich das Gefuehl, dass ich hier Sachen durcheinanderwirble, die nicht zusammengehøren, aber es klingt erstmal plausibel.

Spannend, spannend all dies, nicht wahr.

Aber das hat mich alles etwas von der eigentlichen Aufgabe abgelenkt.

Ich entschied mich letztlich nur bis zu vierstellige Zeichenketten zu untersuchen, 10.000 Datenpunkte sind schon ganz gut. Dafuer aber die Statistik gut zu machen und die Folge bis zur 10-billionsten Stelle (10¹⁰) zu analysieren. Nun ja, streng genommen war es bis zur 10.000.062.095 Stelle. Aber die neu hinzuzufuegenden Elemente werden irgendwann recht lang, der „Fehler“ ist kleiner als 10^-5 und ein bisschen mehr „Statistik“ schadet nicht.

Dazu dann aber mehr beim naechsten Mal.

Ach ja … die Gesamtrechenzeit bei diesen Parametern betrug ca. 15 Stunden, was gut mit den vorher ermittelten Daten uebereinstimmt.

Wie im vorhergehenden Beitrag dieser Reihe beschrieben, braucht mein erster Ansatz, den Computer einfach erstmal die Folge ausrechnen und danach analysieren zu lassen, unheimlich viel Arbeitsspeicher.

Also musste ein neuer Plan her.

Fancypancy meinte ein studierter Experte, dass ich um „streaming“ wohl nicht drumherum komme. Das war dann auch das, was ich mir vorher schon dachte. Anstatt die ganze Folge zu erstellen, lass ich nur jeweils ein (neues) Element nach dem anderen analysieren, bevor das naechste Element erstellt wird.
Das sollte natuerlich deutlich weniger Speicher benøtigen. Wie viel weniger, ist hier zu sehen:

Selbstverstaendlich verhaelt sich die Laenge des naechsten hinzuzufuegenden Elementes nach dem gleichen Gesetz wie die Laenge der gesamten Folge – exponentiell. Aber wenn man die Skala der Ordinate mit der in der Abbildung im oben verlinkten, vorhergehenden Beitrag vergleicht, so sieht man doch wie, absolut gesehen, gewaltig weniger die Laenge des naechsten Elementes im Vergleich zur Laenge der gesamten Folge waechst.
Wenn man den (maximalen) Speicherbedarf betrachtet, so muesste man die Anzahl der Zeichen des als naechstes hinzuzufuegenden Elementes verdreifachen. Dies deswegen, da ich ja immer zwei Elemente im Speicher behalten muss, um das neue (dritte) Element auszurechnen. Daher der Faktor drei. Aber ein Faktor drei … bei exponentiellem Wachstum … tihihi … ich lach mich kaputt … da spricht man nicht drueber ;)

Das (wenn auch exponentielle) Wachstum des naechsten hinzuzufuegenden Elementes geht also deutlich weniger schnell von statten, als das Wachstum der Laenge der gesamten Folge.

Damit war mein Plan zu „streamen“ auf ein solides Fundament gestellt.

Der Analyseteil blieb im Wesentlichen der Gleiche: so viele Zeichen abhacken wie benøtigt, die Haeufigkeit dieser Zahl um eins erhøhen, in der Folge um eins nach rechts ruecken, von vorne beginnen.

Das bedeutete aber nicht, dass es jetzt einfacher war. Ganz im Gegenteil. Ich musste viel mehr ueberlegen um den „streaming“-Teil richtig hin zu bekommen.

Natuerlich war es einfach das naechste Element erst dann auszurechnen und zu analysieren, wenn es benøtigt wird. Dabei muessen aber drei Sachen beachtet werden.
1.: Man benøtigt einen „Ueberhang“ der letzten Zahlen aus dem vorherigen Element.
2.: Aufpassen, dass beim „Ueberhang“ zaehlen nicht doppelt gezaehlt wird.
3.: Was ist, wenn das naechste anzuhaengende Element weniger Zeichen hat, als die Laenge der zu untersuchenden Zeichenketten.

Eine Veranschaulichung zu 1.
Wir nehmen die Zeichenkette 112 und uns interessieren nur ein- und zweistellige Zeichenketten. Dann haben wir darin folgende Verteilung: „1“ = 2 mal, „2“ = 1 mal, „11“ = 1 mal und „12“ = 1 mal
Das naechste Element ware die 3. Wenn wir NUR dieses betrachten wuerden, so wuerden zur obigen Verteilung hinzukommen: „3“ = 1 mal.
Wenn ich aber an die Zeichenkette 112 die 3 anhaenge, so erhalte ich 1123 und wenn ich dies analysiere, so erhalte ich: „1“ = 2 mal, „2“ = 1 mal, „3“ = 1 mal, „11“ = 1 mal, „12“ = 1 mal (bis hierhin also wie gehabt) und zusaetzlich: „23“ = 1 mal.
Beim „Uebergang“ von der 2 zur 3 „entsteht“ eine neue 2-stellige Zahl – die 23. Und die wuerde man uebersehen, wenn man einfach nur das neue Element analysiert.

Bevor man also das neue Element analysiert, muss man an dieses so viele Zeichen vorne ran haengen, wie die Laenge der laengsten zu untersuchenden Zeichenkette ist, minus ein Zeichen. Und das ist das, was ich „Ueberhang“ nenne.

Das ist gar nicht so schwer, sich diesen Ueberhang zu merken. Bei der Analyse muss man einfach nur schauen, wenn die Laenge der von der Folge abgehackten Zahlen, das erste Mal kuerzer wird, als die Laenge der grøszten zu untersuchenden Zeichenkette.

Eine Veranschaulichung zu 2. unter Beruecksichtigung des ersten Punktes.
Wir interessieren uns fuer vier-, drei,- und zweistellige Zeichenketten. Wir nehmen an, dass bis zur 11235813 alles untersucht wurde. Der Ueberhang muesste also 813 werden und das naechste Element wird die 21. Als neue Folge erhalten wir also 81321. Nach dem im vorhergehenden Beitrag vorgestellten Algorithmus untersuche ich dann zunaechst 8132. Davon wuerde die letzte Zahl abgehackt werden um die dreistellige Zeichenkette zu analysieren – also die 813. Hier ist es nun aber so, dass die 813 schon vorher gezaehlt wurde. Bei der Untersuchung der „alten“ Zeichenkette, bevor das neue Element erzeugt wurde. So auch die 81 und die 8.
Im naechsten Schritt waere alles ok mit der 1321 und mit der 132, aber die 13 und die 1 waere auch schon vorher gezaehlt worden.

Der Analysealgorithmus muss das Hinzuaddieren zur Haeufigkeit also rechtzeitig unterbrechen, so lange der Ueberhang noch involviert ist.

Eine Veranschaulichung zu 3.
Hierbei handelt es sich eher um ein technisches, als um ein logisches Hindernis.
Zunaechst denken wir uns das gleiche wie unter 2. Das naechste hinzuzufuegende Element (die 21) ist also ein Zeichen zu kurz um keine Probleme zu bereiten, wenn mich vierstellige Zeichenketten interessieren. Zunaechst ist alles ok. Aus 81321 mache erstmal 8132 und analysiere das. Dann folgt 1321 und dies wird untersucht.
Dann aber ist tritt bei der Umwandlung einer Zeichenkette zu einer Zahl etwas auf, was Probleme bereitet.
Die naechste Zeichenkette waere die 321, also nur noch drei Zeichen lang. Hierbei wuerde der von mir gewaehlte Algorithmus zunaechst annehmen, dass das vierte „Zeichen“ sozusagen „unsichtbar“ ist. Es wuerde also die Zeichenkette „321( )“ umgewandelt werden in … richtig … 321. Danach wuerde das letzte (unsichtbare) Element abgehackt werden und die 321 wuerde nochmal gezaehlt.

So ein Mist aber auch! Nun ja, ich konnte ich auch dieses Problem løsen. Drittens ist vor allem ein Anfangsproblem. Das taucht nicht mehr auf, sobald die neuen Elemente lang genug werden. Dennoch muss es waehrend der ersten Durchlaeufe natuerlich durch eine gut gewaehlte Abbruchbedingung beruecksichtigt werden. Zweitens ist zwar ein permanentes Problem, aber auch hier schafft eine passende Abbruchbedingung das daraus folgende doppelte Zaehlen aus der Welt. Und Erstens ist easy peasy zu bewerkstelligen.

Wie gesagt: dumme Computer! Machen genau das, was man ihnen sagt und nicht das, was man eigentlich møchte, was sie machen sollen.

Letztlich lagerte ich die Analyse des Ueberhangproblems in einen eigenen kleinen Algorithmus aus, der vor der eigentlichen Analyse des neuen Elementes ablaeuft.

Warum schreibe ich das alles … mhm … weil es ja mglw. wen interessiert und dieser weblog auch ein bisschen meiner eigenen Dokumentation dient :)

Falls es jemanden interssiert, so wuerde ich mit Freude den in Python geschriebenen Quellcode des von mir erstellten Programms teilen.
Insb. auch, weil ich hoffe Anregungen zu bekommen.
Es ist immer lehrreich An- und Bemerkungen von auszerhalb des eigenen Kosmos zu erhalten.

In den naechsten Beitraegen werde ich dann endlich die mithilfe dieses Programmes gewonnen Daten (oder vielmehr deren weitergehende Analyse) vorstellen.
Das war ja schlieszlich der eigentliche Grund, warum ich mir diesen ganzen Aufwand gemacht habe.
Das erste Ergebnis ist im Uebrigen schon hier (oben) zu sehen. Ich musste ja schlieszlich erstmal das Element mit 64.651 Stellen (und alle davor) ausrechnen, um euch diesen schønen Zusammenhang zeigen zu kønnen.

Als Anschluss an diesen Beitrag frage ich mich, ob es nicht doch doch nur die Ruhe vor dem Sturm ist.

Denn die Geister die wir riefen …

… dass das ja nur „bei denen“ so schlimm ist, aber nicht bei uns, der møge doch bitte diesen Artikel lesen.

Es steht ja eigentlich nichts Neues drin, aber es ist wichtig, dass wir das nicht aus den Augen verlieren.

Einen Computer was ausrechnen zu lassen hørt sich ja erstmal nicht so schwer an. Und ist es auch nicht mit so einer einfachen rekursiven Folge. Also programmierte ich das erstmal so geradlinig.

Und die einzelnen Elemente wurden immer laenger und laenger und mit ihnen die Folge.

Und auch die Analyse wie oft eine Zeichenkette vorkommt ist erstmal recht simpel:
– Nimm vom Anfang der Folge so viele Zeichen wie du brauchst.
– Welche Zeichenkette ist das?
– Setze den Zaehler fuer diese Zeichenkette um eins nach oben.
– Gehe in der Folge einen Schritt nach rechts und beginne von vorn.
Dabei dachte ich so, dass ich wenn ich das Vorkommen bspw. aller sechsstelligen Zeichenketten untersuchen will, dann sozusagen im Vorbeigehen auch gleich das Vorkommen aller fuenf-, vier-, drei-, zwei- und einstelligen Zeichenketten untersuchen kønnte. So schwer ist das nicht, wenn man sich naemlich im ersten Schritt die zu untersuchende Zeichenkette (bspw. mit sechs Zeichen) aus der Folge extrahiert hat, dann muss man von dieser Zeichenkette immer nur eins „abhacken“ bis nichts mehr da ist.

Ein Beispiel. Die Folge sei „1123581221“ und die Aufgabe sei alle Zeichenkette mit sechs Zeichen oder weniger zu untersuchen.
– Extrahiere die Zeichenkette „112358“ von der Folge.
– Schema F: der numerische Wert dieser Zeichenkette ist 112358; setze den Zaehler fuer diesen Wert um eins nach oben.
– Plan 9: Entferne von „112358“ das letzte Glied und erhalte die neue Zeichenkette „11235“; verfahre nach Schema F mit der nun 5-stelligen Zahl.
– Verfahre nach Plan 9 und erhalte die neue Zeichenkette „1123“; verfahre nach Schema F mit der nun 4-stelligen Zahl.
– Wiederhole dies so lange, bis die neue Zeichenkette nur noch ein Zeichen lang ist.
– Hacke nun von der ganzen Folge (!) das erste Glied ab und beginne von vorne.
– Dies ist so lange zu wiederholen, bis die gesamte Zeichenkette „verbraucht“ ist.

Durch dieses Verfahren vermeide ich eine doppelte Zaehlung bereits gezaehlter Zeichenketten, da beim naechsten Durchlauf durch die gesamten Schritte alles um eins nach rechts „verschoben“ ist und somit neue sechs- , fuenf-, vier- usw. -stellige Zeichenketten gebildet werden.

Ein Problem ergibt sich aus dieser Vorgehensweise: die Umwandlung der Zeichenkette in den numerischen Wert wandelt Zeichenketten mit fuehrenden Nullen in numerische Werte um, die die falsche (eine kleinere) Laenge haben. Aus der Zeichenkette „0007“ wird der Wert 7.
Dadurch wuerde also in diesem Falle bei den vierstelligen Zeichenketten einmal zu wenig und bei den einstelligen Zeichenketten einmal zu viel gezaehlt.
Eine Variation der Konsequenz ist, dass Zeichenketten die mehr als eine Stelle haben, erst dann gezaehlt werden, wenn das erste Zeichen keine Null ist.
Dreistellige Zeichenketten werden bspw. erst ab der 100 gezaehlt, vierstellige ab der 1000 usw. Dadurch werden 10% der Daten fuer x-stellige Zeichenketten nicht gezaehlt, bzw. falsch zugeordnet werden.

Beides kann man relativ brutal umgehen, indem man die Tabelle, in der die Haeufigkeit einer gewissen Zeichenkette gespeichert wird, massiv erweitert.
Anstatt (nur bis alle zweistelligen Ziffern) …

0	23 mal
1	12 mal
2	7 mal
…	…
98	11 mal
99	44 mal

… also eine erweiterte Tabelle:

einstellige Zeichenkette	Vorkommen		zweistellige Zeichenkette	Vorkommen
0	23 mal		00	5 mal
1	12 mal		01	1 mal
2	7 mal		02	18 mal
…	…		…	…
9	15 mal		09	23 mal
			10	99 mal
			11	3 mal
			…	…
			98	11 mal
			99	44 mal

Man beachte, dass die Werte fuer die Zeichenkette „1“ natuerlich anders sind, als fuer die Zeichenkette „01“.
Am auffaelligsten ist natuerlich, dass Erstere ca. 10 mal haeufiger Vorkommen sollte als Letztere. Es gibt ja 10 mal so viele zweistellige Zeichenketten, wie einstellige. Mit all diesen muss sich die spezifische Zeichenkette „01“ das Vorkommen „teilen“.

Der Vorteil dieser Methode: ich muss mir keinen Kopf mehr machen, dass der numerische Wert von „0007“ eine 7 ist. Ich teile dem Programm einfach mit, dass es gefaelligst in der Spalte fuer vierstellige Zeichenketten den Wert von Sieben um eins erhøhen soll und ich behalte in Erinnerung, dass es sich dabei eigentlich um die „0007“ handelt.
Oder anders ausgedrueckt: ich kann einfach die Umwandlung von Zeichenkette in numerischen Wert beibehalten und muss mir da nix extra ausdenken, wie ich dem Computer klarmache, dass fuehrende Nullen wichtig sind.
Dadurch wird natuerlich auch kein Wert einer weniger langen Zeichenkette mehrfach gezaehlt. Bei jeder x-stelligen Zeichenkette wird immer nur der Eintrag in der richtigen Spalte der Tabelle gemacht.

Zwei Nachteile hat diese Methode.
1.: Will ich das Vorkommen zweistelliger Zeichenketten anstatt nur einstelliger Zeichenketten untersuchen, erhøht sich mein Speicherplatzbedarf schlagartig um das zehnfache. Will ich dreistellige (und zwei- und einstellige) Zeichenketten untersuchen so brauche ich 100 mal mehr Speicherplatz, wie als wenn ich nur einstellige Zeichenketten untersuchen wuerde; usw. usf.
2.: Das Speichermanagement wird vermutlich einen signifikanten Teil der Rechenzeit beanspruchen. Mit jeder neu untersuchten Zeichenkette (also nach jedem „abhacken“ eines Zeichens), muss der Rechner zu einer ganz anderen Spalte in der Tabelle gehen, dort das richtige Element finden und den Zaehler um eins erhøhen. Der Rechner muss also auf x-vielen Tabellen gleichzeitig arbeiten und nicht nur auf einer.

Letztlich dachte ich mir aber, dass die Vorteile (das richtige Zaehlen und dass ich dem Programm nicht die Wichtigkeit fuehrender Nullen beibringen musste) die Nachteile ueberwiegen. Speicherplatz ist heutzutage wahrlich kein Problem und wie lange das Rumrødeln auf den Tabellen dauert … mhm … davon hab ich keine Ahnung, aber ich wollten den Rechner ohnehin viele Stunden rechnen lassen.

 

Soweit dazu.

 

Als ersten Versuch erstellte ich also ein Programm welches mir eine immer laenger und laenger werdende Zeichenkette erstellte. Wenn diese Zeichenkette eine bestimmte Laenge erreicht hat, so stoppte das Programm mit dem weiteren Hinzufuegen von Zeichen und  zerhackte diese Kette dann in kleine Stuecke und untersuchte diese.
Im ersten Satz erkennt man auch den Fehler dieses Programms. Oder weniger ein Fehler, als vielmehr den Grund, warum ich dieses Programm nicht fuer die eigentliche Arbeit benutzen konnte.

Auch wenn jetzt ein Experte sagen kønnte „das kommt auf die Codierung an“, so belegt im schlimmsten Fall eine 2-stellige Zeichenkette 2 Byte Speicherplatz. Eine hundert-stellige Zeichenkette also 100 Byte usw. Wenn ich also die Fibonaccifolge bis zur 10-milliardsten Stelle untersuchen will, dann belegt diese Folge im schlimmsten Fall 10 Gigabyte im Arbeitsspeicher.
Weil ich grafische Veranschaulichungen so mag, hier eine eher sinnlose Darstellung dieses Sachverhaltes:

Tihihi … Man beachte bitte die doppellogarithmisch Darstellung. Der Speicherplatzbedarf nimmt also mit jeder Potenz der Laenge der Folge exponentiell zu. .oO(Hach wie schøn man einfache Zusammenhaenge doch unnøtig aufblaehen kann … Laenge der Folge in Abhaengigkeit von der Laenge der Folge … tihihi.)
In der Grafik ist der maximale Speicherplatzbedarf nur bis zu einer Fibonaccifolgenlaenge von 100 Millionen Zeichen dargestellt. Deswegen „sieht“ man noch nicht die oben erwaehnten 10 GB benøtigten Arbeitsspeicher. Meine Leserinnen und Leser møgen dies doch bitte selbst extrapolieren.

Ach so, der Speicher den die oben erwaehnte Tabelle braucht ist dagegen irrelevant.

Wieauchimmer, so viel Arbeitsspeicher habe ich leider nicht. Deswegen musste das Programm was das Erstellen der Zahl und einen Teil der Analyse angeht komplett umgeschrieben werden. Dazu aber im naechsten Artikel mehr.

Fuer dieses Mal ist festzuhalten: Ein Computer macht genau das was in den Anweisungen steht und erstmal nicht das, was man will, was der Computer machen soll. Deswegen muss man jedes noch so einfache Problem in kleine Schritt zerlegen und sich ueberlegen ob da nicht Sachen dabei sind, die der Computer dann genau so macht wie man es programmiert, die aber nicht der Løsung des Problems zutraeglich sind. Oder anders: man muss erstmal so dumm denken lernen wie ein Computer stupide das macht was man programmiert. Einen Teil dieses Prozess fuer diese spezielle Aufgabe habe ich hier dargelegt.

Parmanand Singh schreibt in der Historia Mathematica, Volume 12, Issue 3, August 1985, Seiten 229–244 in seinem Artikel „The so-called fibonacci numbers in ancient and medieval India“ (Volltext scheint fuer die Allgemeinheit verfuegbar zu sein), dass bereits Virahanka, Gopala und auch Hemachandra vor Leonardo da Pisa diese mathematische Folge von Zahlen und deren Bildungsgesetz angaben. Wohl auch in Europa war die Folge in der Antike bereits Nikomachos von Gerasa bekannt. Aber wie so oft, fallen Ruhm und Ehre wem anders zu, weil irgendwann mal irgendwer zu faul war ordentliche Literaturrecherche zu machen und hinterher will es wieder keiner gewesen sein und keiner gibt den Fehler zu und deswegen wird es bis heute nicht ordentlich gemacht. Aber letztlich ist’s ja doch auch nicht so richtig relevant, was fuer einen Namen das Kind traegt … wohohoho … DAS ist natuerlich eine ganz andere Diskussion im Zusammenhang mit wirklichen Kindern; aber darum soll es hier nicht gehen. Deswegen halte ich mich an diesen nach dem „filius Bonacii“ (Sohn des Bonacii) gegebenen Namen.

Die Fibonaccifolge ist eine so schøn einfache Folge. Das naechste Element bildet sich aus der Summe der ersten beiden Elemente. Aus 1 und 1 mach 2. Aus 1 und 2 mach 3. Aus 2 und 3 mach 5. Aus 3 und 5 mach 8 usw. ad infinitum. Hier sind mal die ersten Glieder:

1, 1, 2, 3, 5, 8, 13, 21, 33, 54, 87, 141, 228, 369, 597, 966, 1563 … … …

Diese Reihe waechst also relativ rasant.

Die Zahlen alle hintereinandergeschrieben ergeben eine neue Zahl. Im obigen Beispiel waere das 11235813213354871412283695979661563. Bis zum 17. Element „bildet“ die Fibonaccifolge eine 35-stellige Zahl.

Alles klar, alles einfach. Ich erzaehle das, um das anstehende Problem besser zu verdeutlichen.

In kurz (und mathematisch nicht ganz sauber formuliert) beschaeftigte mich seit Jahren der Gedanke, ob alle Zahlen gleich haeufig in der Fibonaccifolge vorkommen.
Oder anders: wie oft kommt mein Geburtsdatum in der Fibonaccifolge bis zur 100-millionsten Stelle vor und kommt jede andere achtstellige Zahl genauso haeufig vor.

AHAHAHA! In der zweiten Formulierung steckt schon etwas korrektere Mathematik – die Haeufigkeit einer Zahl.
Natuerlich kommen nicht alle Zahlen gleich oft vor bis zu einer gegebenen Stelle der Folge.
Zur Veranschaulichung denken wir uns 4-stellige Zahlen; bspw. die 1234 oder die 9999. Dann kann es natuerlich schon sein, dass die 1234 bis zu einer bestimmten Laenge der Folge exakt genau so oft drin ist, wie die 9999, oder die 8765. Aber von allen 4-stelligen Zahlen wird sicherlich die eine oder andere øfter oder weniger oft bis zu dieser Stelle der Folge drin sein.
„Genauso haeufig“ wuerde also auf die Frage hinaus laufen, ob das Vorkommen aller Zahlen bis zu einer gegebenen Laenge der Fibonaccifolge normalverteilt ist.

Und hier kønnte ein richtiger Mathematiker mich verbessern. Zum Ersten gibt es es einen ganzen Haufen von Wahrscheinlichkeitsverteilungen. Ich habe nicht die leiseste Ahnung, ob die Normalverteilung die Richtige ist (sein kønnte). Bei der Wahl der Verteilung folgte ich dem Indifferenzprinzip (und dem Einfachheits- bzw. Faulheitsprinzip: keine Ahnung haben = nimm das was du kennst).
Zum Zweiten ist die Normalverteilung eine stetige Wahrscheinlichkeitsverteilung. Bei dem Problem handelt es sich aber um ein „diskretes Problem“. Ich sollte das also dahingehend umformulieren, ob sich das Vorkommen aller Zahlen einer Normalverteilung angleicht. Ich habe aber wiederum keinen blassen Schimmer inwiefern das gerechtfertigt ist (sein kønnte).
Das erinnert mich etwas daran, dass ich erstmal zeigen sollte, dass es eine Løsung gibt bevor ich mich an das Berechnen dieser Løsung mache.

Wieauchimmer, mich duenkt, dass dieses Problem mit dem Problem verwandt ist, ob eine Zahl normal ist. Auch bei dieser Behauptung bleibe ich mir (und euch, meinen lieben Leserinnen und Lesern) den Beweis der Richtigkeit derselben schuldig.

Im uebrigen ist das bei Pi (und anderen irrationalen Zahlen) eine offene Frage. Bis zur 100-millionsten Stelle scheint es aber wohl ganz gut zu passen.

Das Problem laeszt sich also auf zwei einfache Probleme herunterbrechen:
1.: addiere zwei Zahlen nach einem bestimmten Schema und haenge die Summe an die Kette ran; brich ab, wenn die Kette eine bestimmte Laenge hat;
2.: zaehle wie oft gewisse Zahlen vorkommen.

„Einfach“ in so fern, dass man sich das leicht vorstellen kann. Am Beispiel oben sieht man ja aber, wie rasant die einzelnen Elemente wachsen. Zur Addition wuerde ich also einen Computer empfehlen. Und eine Zahl mit 100 Millionen stellen zu untersuchen ist auch recht langwierig. Da der Computer ohnehin schon zur Hand ist, sollte der gleich auch zur Analyse benutzt werden. Schlieszlich handelt es sich um ein Zahlenverarbeitungsproblem. Dafuer wurden die Dinger schlieszlich erfunden.

Eigentlich greife ich mit all diesen Ausfuehrungen schon viel zu weit vor. Ich war ja dabei, dass mir das Problem seit Jahren im Kopf rumspukte. Ich hatte aber nie die Musze, mich da mal naeher mit zu beschaeftigen. Wusste ich doch, dass ich dafuer zumindest rudimentaere Programmierkenntnisse haben muss.

Dann aber geschah es, dass ich vor einiger Zeit bei einem Quiz dabei war. Ich will jetzt nicht sagen, dass ich „mitgeschleppt“ wurde. Ich bin da aus eigener Initiative mitgegangen. Aber mein Wissen zu norwegischen Gerichten, Werbespruechen oder anderen bei solchen Quiz‘ gefragten Sachen halten sich doch sehr in Grenzen.

Ich hatte aber einen Stift in der Hand und eine Serviette vor mir liegen. Zunaechst malte ich nur die ueblichen Krusedull (ein Wort, welches ich sehr sehr toll finde). Etwas im Geiste finge ich dann an, die ersten Elemente der Folge aufzuschreiben. Dann begann ich noch mehr Elemente ordentlich auszurechnen. Ich schrieb die Folge bis zu einer gewissen Laenge auf (mich duenkt bis zur 39. Stelle oder so) und zaehlte, wie oft die Zahlen 0 bis 9 darin vorkamen. Dannn zeichnete ich ein Histogramm.
Und dann geschah das, was i.A. als Nerd-Sniping bekannt ist. Ich fing an mir mit meinen (mittlerweile vorhandenen) rudimentaeren (wirklich nicht mehr!) Programmierkenntnissen Gedanken ueber eine Automatisierung des Ganzen zu machen. Nebenbei lief das Quiz natuerlich weiter und ich warf auch ab und zu mal ein Kommentar ein.

Hier ist die Arbeit des beschriebenen Abends zu sehen:

Damit løse ich natuerlich nicht das eigentliche mathematische Problem dahinter. Aber ich sage mal so. Wenn ich sehe, dass sich die Haeufigkeiten fuer bspw. alle vierstelligen Zahlen bis sagen wir zur 100-millionsten Stelle der Fibonaccifolge einer Normalverteilung genuegend angleichen, dann sehe ich das Problem fuer meine Beduerfnisse als geløst an.

Eine technische Sache noch an dieser Stelle. Bisher schrieb ich bspw. „4-stellige Zahlen“. Natuerlich sind damit 4-stellige Zeichenketten gemeint.
4-stellige Zahlen beginnen bei der 1000 und enden mit der 9999.
Bei der „0007“ hingegen handelt es sich um eine 4-stellige Zeichenkette, auch wenn die Zahl selber einstellig – die Sieben eben – ist.
Wenn man sich auf die Ziffern 0 bis 9 als Zeichen beschraenkt beginnen 4-stellige Zeichenketten bei der „0000“ und enden bei der „9999“. Man hat also insgesamt 10.000 verschiedene 4-stellige Zeichenketten.
Ich entdeckte dieses Problem erst als ich schon „mittendrin“ war. Sicherlich auch dadurch bedingt, weil ich die ganze Zeit ja irgendwie mit Zahlen  arbeite. Da musste ich durch „Fehler in den Resultaten“ erstmal auf den Unterschied zwischen Zahl und Zeichenkette gestoszen werden.

Aber genug fuer heute.
Die naechsten Beitraege werden sich zunaechst dem „technischen Hintergrund“ widmen, bevor ich mich an die Dartellung der spannenden (und schønen) Ergebnisse mache.

Im ersten Beitrag dieser Reihe versprach ich, dass der Einfluss des hiesigen Filmfestivals in einem eigenen Beitrag betrachtet wird.

Nun ist es aber so, dass der Einfluss auf die Gesamtzahl der Kinobesuche und auf den durchschnittlichen Kartenpreis bereits in besagtem ersten Beitrag betrachtet wurde; es werden mehr Besuche insgesamt und der durchschnittliche Kartenpreis nimmt etwas ab.

Im zweiten Beitrag dann wurde klar, dass ich deswegen mehr Filme im Nova sehe, als im Prinsen. Ein Einfluss darauf, in welchem Saal ich Filme schaue gibt es nicht, da im gesamten Nova nur Festivalsfilme laufen.

Bisher war ich im Wesentlichen ohne andere Leute in Festivalfilmen. Deswegen ist der Einfluss des Festivals derart, dass der blaue Teil der Balken im erste Bild des dritten Beitrages zunimmt.
Mhm … ich bin mal positiv und nehme an, dass ich mit besagter „Newcomer(in)“ im naechsten Jahr mehrere Kosmoramafilme schauen werde. Damit duerfte oben besagter Einfluss sich ausgleichen, aber ihr Anteil an der dritten Grafik wird dadurch natuerlich rasant zunehmen.

Bei der Untersuchung der Tage und Monate im vierten Beitrag stellte sich schlieszlich heraus, dass ich durch Kosmorama ueberdurchschnittlich viele Filme im April (bzw. Mai) sehe. Dieses Jahr wird das Festival im Maerz stattfinden und sich sicherlich entsprechend bemerkbar machen.
Im allgemeinen gibt es keinen Einfluss auf die Tage, denn ich schaue an allen Festivaltagen ungefaehr gleich viele Filme.

Aufgrund des Ursachen des Resultats verzichtete ich bei der Betrachtung der Uhrzeiten im fuenften Beitrag darauf, mehr als das dort Gezeigte und Gesagte einzufuegen.

Dies wird nun hier, nachgeholt.

Da zu der Zeit als ich diesen Artikel schreibe (01. Oktober 2014) das Jahr 2014 noch nicht abgeschlossen ist, sind in folgendem die Daten fuer 2013 zu sehen.

Die blauen Balken repraesentieren ausschlieszlich die waehrend Kosmorama geschauten Filme, waehrend die roten Balken alle in 2013 geschauten Filme darstellen (inkl. der Kosmoramafilm!).

Abgesehen davon, dass Kosmoramafilme teilweise fuer die einzigen Eintraege zu gewissen Uhrzeiten verantwortlich sind, so sieht man, dass das Festival keinen (!) Einfluss auf die Lage der Hauptpeaks hat. Offensichtlich planen die Festivalverantwortlichen mit ein, dass man zwar am Beginn eines Tages immer gut durchgeplant alles schauen kann, aber dann Unregelmaeszigkeiten im Plan durchaus willkommen sind, denn man braucht ja auch mal ’ne Pause, nicht wahr.
Und selbst wenn die Kosmoramafilme zu „den ueblichen Zeiten“ gezeigt werden wuerden, so wuerde es in der Summe einem „konstanten Untergrund“ entsprechen und die Lage der Peaks nicht beeinflussen.

 

An dieser ganzen Datensammlung ist durchaus interessant, dass ich das Genre der geschauten Filme nicht angebe. Das ist fuer mich i.A. einfach nicht von Belang. Mal davon abgesehen, dass ich Schreckfilme seit einigen Jahren eher vermeide (ich bin halt nicht mehr der Juengste) und mich romantische Komødien nicht interessieren. Aber auch da gibt es Ausnahmen. Letztlich ist ein Film entweder eine gute Unterhaltung, eine „Freude fuer die Sinne, den Geist und das aestethische Empfinden“ (wie „Kunst“ im Allgemeinen) oder Beides, oder ein Film ist es nicht. Da kommt es nicht auf das Genre an.

 

Mit diesem Beitrag møchte ich diese kleine Serie abschlieszen. In zehn Jahren oder so folgt mglw. ein Update. Ich hoffe dann nicht schon wieder irgendwie im Zuge eines emotional all zu schweren Umbruchs.

Ich hoffe es machte euch, meinen lieben Leserinnen und Lesern, etwas Freude in die Welt der (meiner) Kinometadaten einzutauchen. Zumindest ich fand es schon ziemlich erstaunlich, was man so alles da heraus holen kann.