Søren in Norwegen

Nach der nøtigen Verallgemeinerung vom letzten Mal kann ich endlich zu den zweidimensionalen Falschfarbenbildern kommen. Nur eine kleine Sache muss ich noch erwaehnen. Meine Lieblingsfarbpalette fuer Falschfarbenbilder hat gewisse Probleme (in kurz: sie luegt mich an und gaukelt mir Sachen vor die gar nicht da sind; schau bspw. hier, etwas technischer hier). Ich wusste davon seit einigen Jahren. Dinge die einem am Herzen liegen, gibt man nur nicht so schnell auf. Aber nun endlich habe ich mich dazu durchgerungen eine andere Farbpalette zu benutzen, die nicht mit diesen Problemen einher kommt.

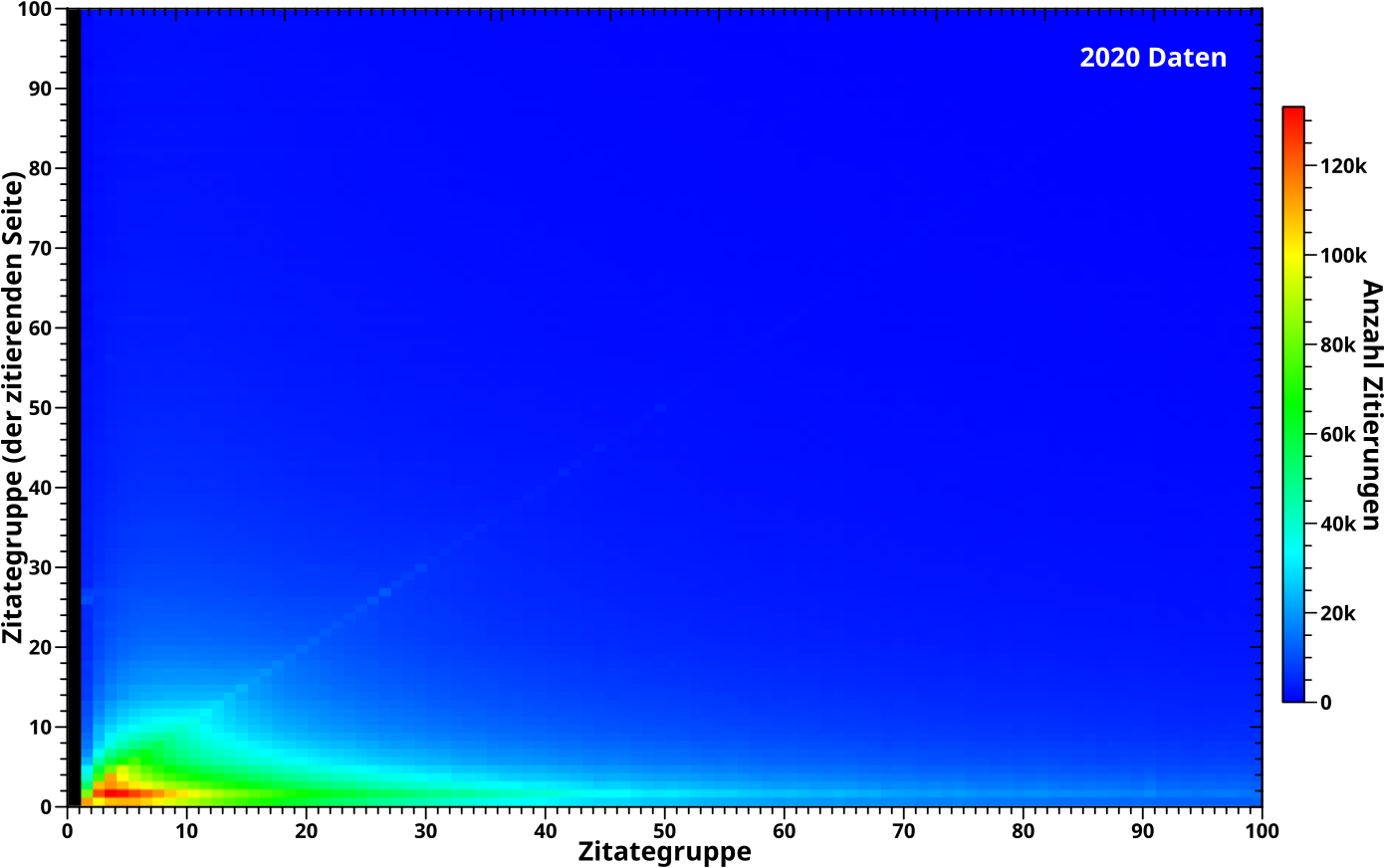
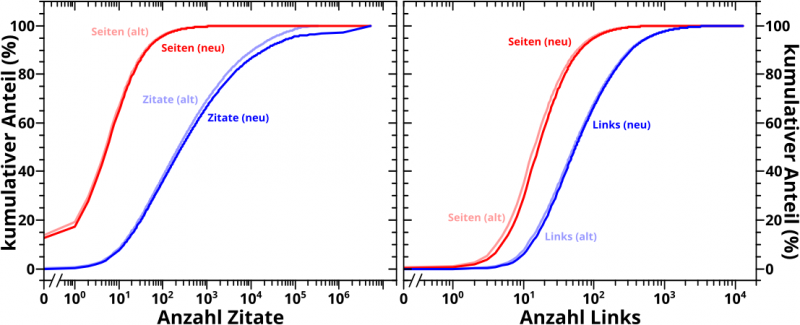
Hier ein Vergleich von alt und neu:

Es ist gerade noch nicht so wichtig, was man da sieht (denn ich komme gleich darauf zurueck). Wichtig ist, dass die Farbpalette von blau bis rot im hellgruenen Bereich eine viel høhere Intensitaet vermuten laeszt, als tatsaechlich da ist. Das ist nur das auffaelligste Merkmal (es gibt noch andere, wenn man genau hinschaut) und ich werde hier nicht darauf eingehen, inwiefern das Information hinzufuegt, die so nicht vorliegt. Aber all das tritt bei Benutzung der neuen Farbpalette nicht mehr auf.

Das soll dazu reichen und ich gehe sofort zum eigentlichen Thema ueber: Falschfarbenbilder die zeigen welche Seiten von welchen anderen Seiten zitiert werden.
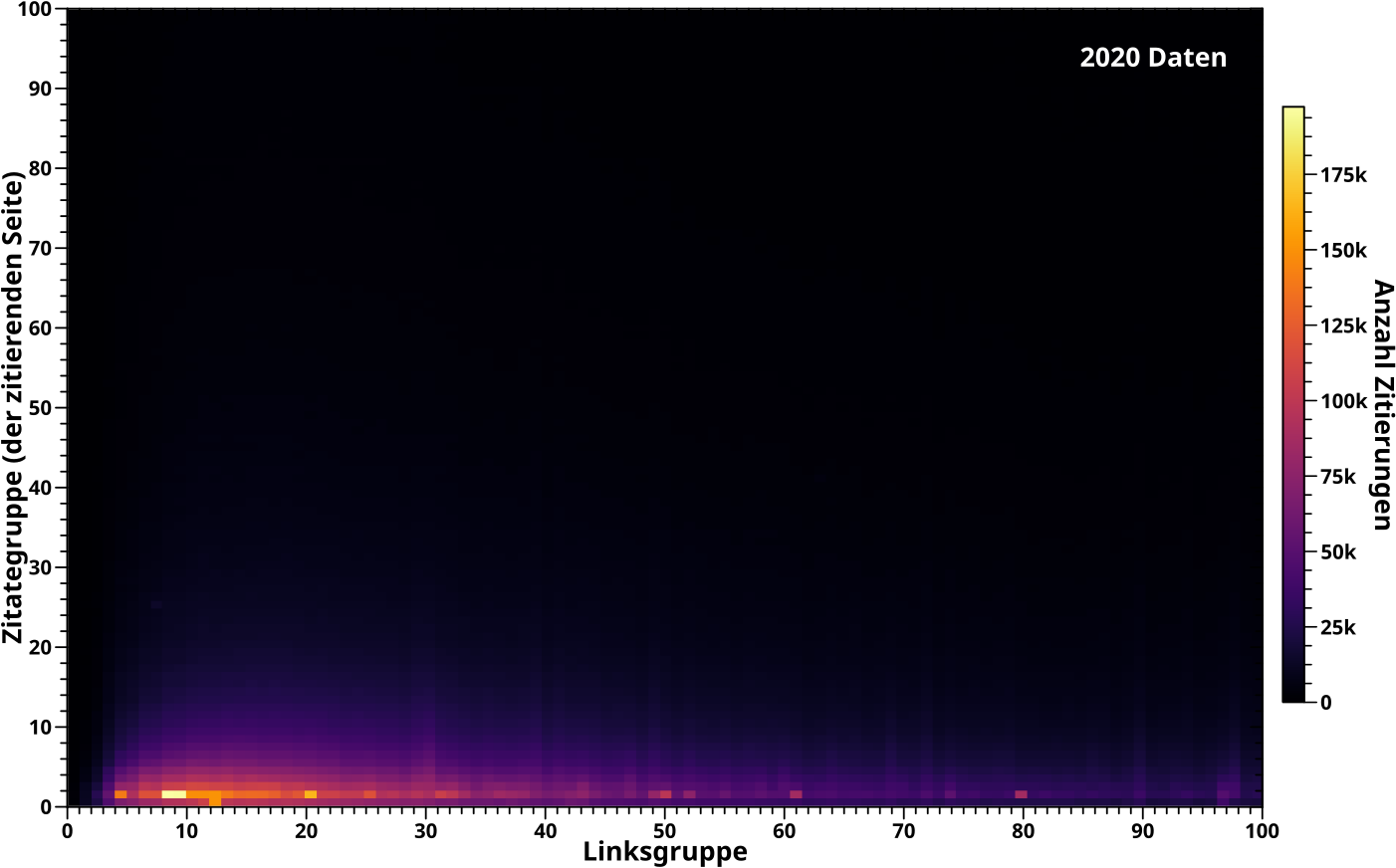
Bereits damals stellte ich fest, dass man im Wesentlichen nur schwarz sieht (Wortspielkasse), wenn man sich alles anschaut und die „Action“ um den Ursprung herum passiert. Daran hat sich auch mit den 2023-Daten nix geaendert und deswegen zeige ich hier nur Bilder die sich auf die ersten hundert Bedeutungsgruppen (zum Quadrat) konzentrieren.

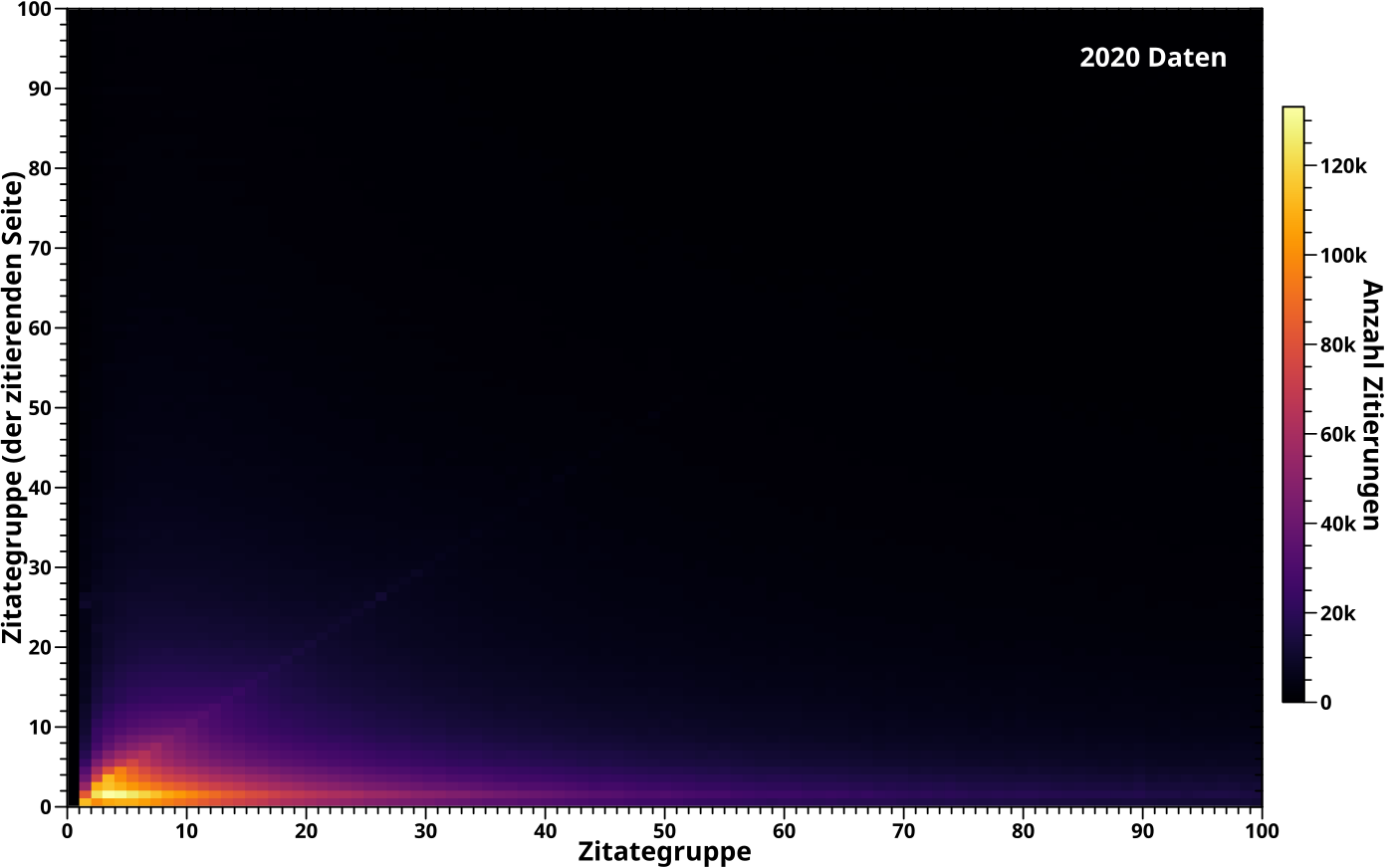
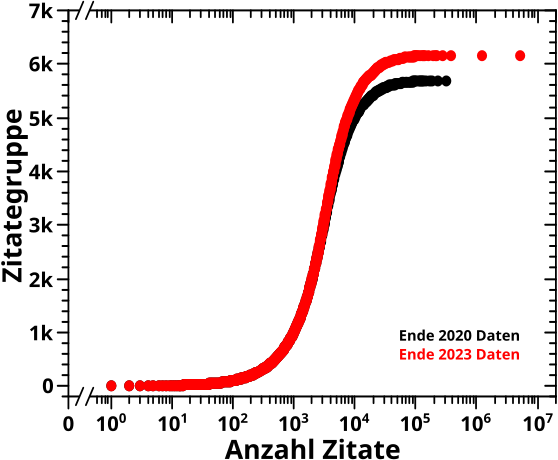
Fuer den Reproduzierbarkeitsteil (aber mit neuen Farben) der Vergleich des Zitate-ueber-Zitate-Bildes:

„OI! Da aendert sich doch aber gewaltig viel!“ kønnte man da sagen, denn die Intensitaet nimmt stark ab. Ihr meine lieben und aufmerksamen Leserinnen und Leser seht aber sicherlich sofort, dass sich auch die Farbskala gewaltig aendert. Und wenn man das vergleicht, dann ist das doch sehr aehnlich.
Der Grund fuer die viel weiter reichende Farbskala bei den 2023-Daten liegt in der einen Wikipedia Hauptseite die insgesamt ueber 5 Millionen Zitate erhaelt und in den 2020-Daten nicht dabei ist. Das ist buchstaeblich nur die allerletzte Spalte, und auch da nur ca. die ersten 23 Pixel, die den kompletten (Farb)Bereich voll ausnutzen. Die Farbwerte (aber nicht die Zahlenwerte) aller anderen Pixel ist dementsprechend herunter gesetzt. Die Aenderung ist somit ein technisches Artefakt und liegt nicht an den allgemeinen (!) 2023-Daten an sich. Wenn man besagte Hauptseite (und noch eine zweite Seite mit ueber 1 Million Zitaten, bei der ich aber nicht schaute um was es sich dabei handelt) entfernt, ist alles im Wesentlichen wie vorher. Und hier ist das entfernen vøllig OK, da es sich ja im einen tatsaechlichen Ausreiszer handelt, der gar nichts ueber die generelle Situation aussagt.

Von dem leicht zu korrigierenden, technischen Artefakt abgesehen passiert auch bei den 2023-Daten nicht viel. Das Intensitaetsmaximum liegt beide Male um 3 Zitate auf der Abzsisse und 1 Zitat auf der Ordinate und der leuchtende „Blob“ zieht sich parallel zur x-Achse ein wenig in die Laenge und bildet einen „duennen Schwanz“ aus.

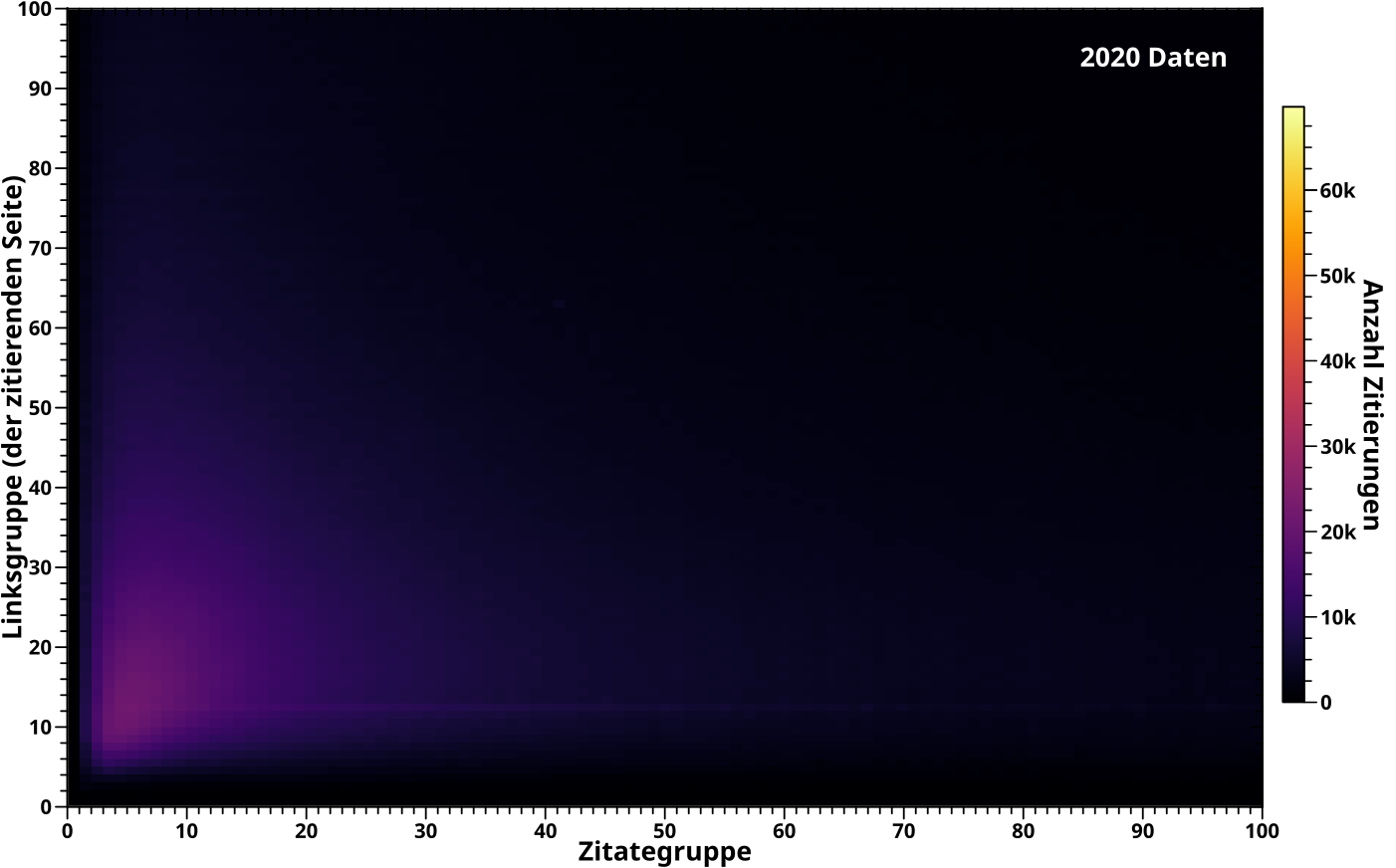
Wenn man sich aber das Links-ueber-Zitate Bild anschaut wird’s in den 2020-Daten spannend:

Zum Einen verteilt sich die „Action“ mehr; der „Blob“ ist viel ausgedehnter. Zum Zweiten leigt das Maximum bei ungefahr 4 Zitaten auf der Abzisse und ungefaehr 11 Links auf der Ordinate. Zum Dritten dehnt sich der „Blob“ zwar relativ gleichmaeszig entlang beider Achsen aus, scheint die Richtung parallel zur Ordinate aber ein klein wenig zu bevorzugen. All das ist voll aufregend und gehørt untersucht. Aber nicht (mehr) von mir und nicht an dieser Stelle.
Abschlieszend zu diesem Bild ist wieder nur zu sagen, dass es keinen Unterschied in den 2023-Daten gibt. Die Aenderung der Intensitaet ist auch hier wieder nur ein Artefakt.

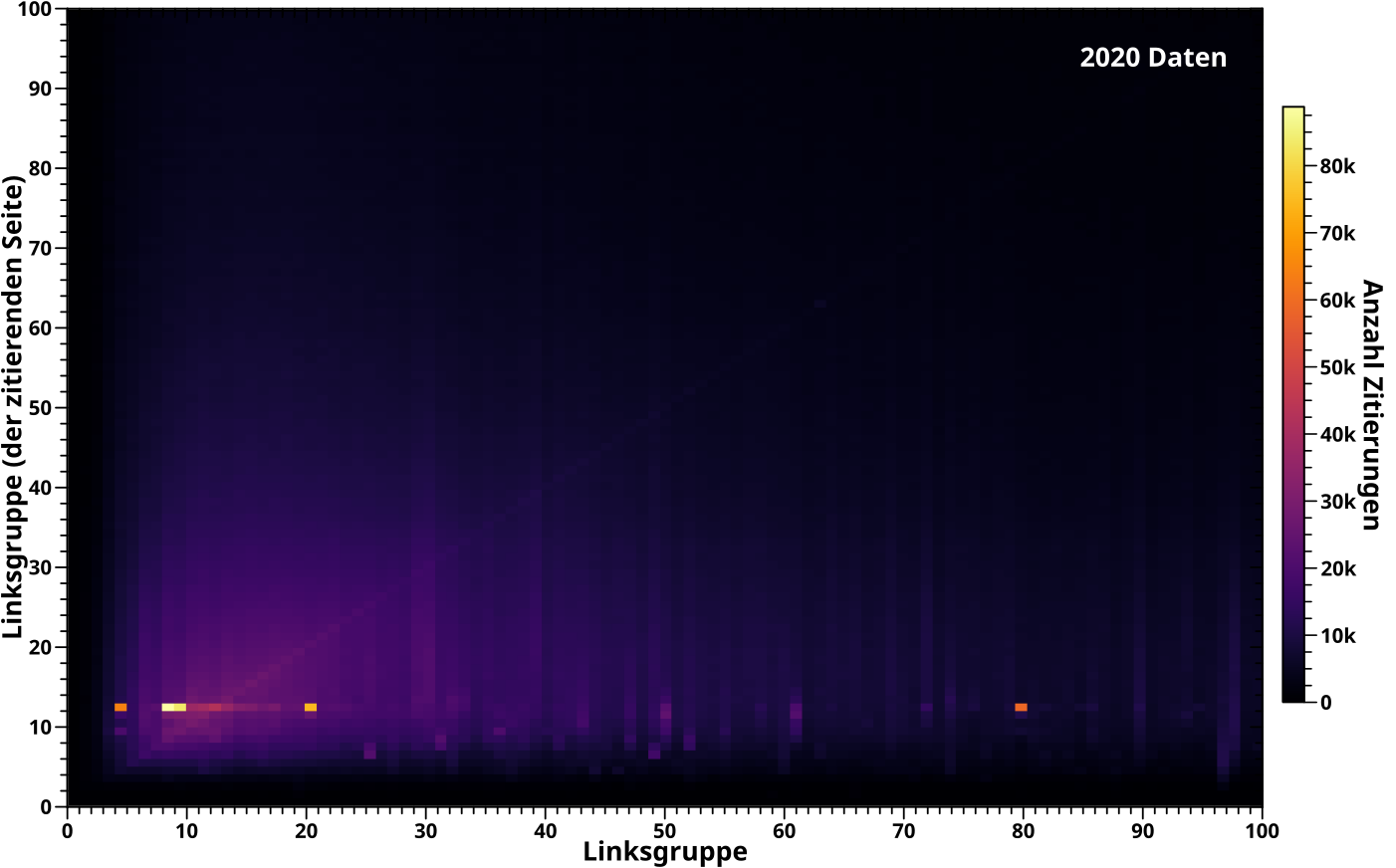
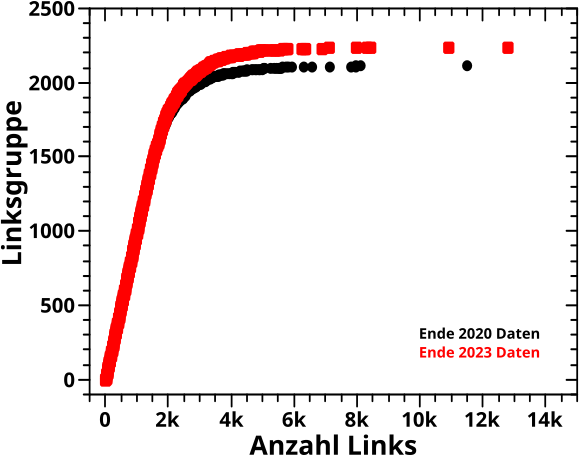
Auf zum Links-ueber-Links Bild:

Ich gehe jetzt nicht im Detail auf alle Merkmale ein, an den 2020-Daten sieht man aber leicht, dass es noch andere Informationen offenbart als beide vorherigen Darstellungen.
Interessant ist die helle, unterbrochene Linie, parallel zur Abzsisse, bei 12 Links auf der Ordinate. Dort treten etliche Pixel _deutlich_ hervor. Das ist bestimmt ein weiteres Artefakt und es wuerde mich nicht wundern, wenn es sich dabei um Seiten handelt, die ich hier als „Information Operations“ bezeichnete. Diesmal liegt das Artefakt aber nicht in der Darstellung, sondern in den Daten … andererseits dachte ich auch beim „São-Paulo-FC“-Phaenomen, dass es sich dabei um ein Artefakt handelt und das stellte sich dann nur als extremste Ausfuehrung einer systematischen Sache heraus.

An dieser Linie sieht man auch die einzigen zwei echten Unterschiede zu den 2023-Daten. Zum Einen scheint die Linie um eins nach oben zu „springen“. Ich wuerde zunaechst nicht ausschlieszen, dass ich da einen Fehler gemacht habe. Denke aber nicht, dass dem so ist.
Vielmehr vermute ich, dass der Hintergrund wieder die Wikipedia Hauptseite ist. Ein Link dahin scheint bei den 2023-Daten in (fast) allen Seiten drin zu sein (denn andernfalls haette die nicht so viele Zitate). Wenn besagter Link zwischen Ende 2020 und Ende 2023 automatisch zu allen Seiten hinzugefuegt wurde, heiszt das ebenso, dass die Anzahl der Links aller Seiten um eins nach oben geht. Das wuerde die hier nicht mal erwaehnte, weil so schwache, ganz leichte Verschiebung der roten Kurve erklaeren … wenn man genau hinschaut, scheinen dort alle Seiten um eins nach rechts gehuepft zu sein. Aber auch das werde ich mir nicht weiter anschauen … ich erwaehnte es nur als plausiblen Mechanismus, der die Unterschiede einfach erklaeren wuerde.
An der Linie sieht man noch einen weiteren Unterschied: die Position der hellen Punkte verschiebt sich auch entlang der Linie (bzw. verschwinden diese zum Teil vøllig). Das sieht mir nach ’ner „Hausmeisteraktion“ bei der Wikipedia aus, bei der bspw. „Information Operations“-Seiten geløscht wurden. Ein paar solcher Seiten konnten „entkommen“, bzw. rutschten vermutlich gerade unter die Erkennungsgrenze die fuer solche Seiten festgelegt wurde.

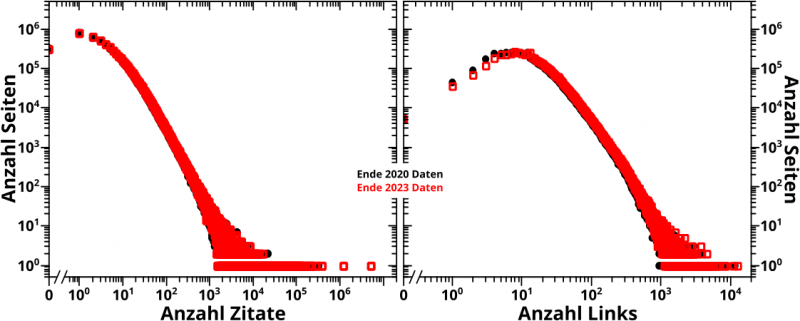
Und nun noch schnell das Zitate-ueber-Links Bild:

Man sieht an den 2020-Daten, dass es von allen drei neuen Achsenbedeutungskombinationen am meisten dem Zitate-ueber-Zitate Bild zu aehneln scheint. Es gibt aber Unterschiede die sich lohnen naeher zu betrachten … ihr, meine lieben Leser und Leserinnen ahnt es aber sicherlich schon: das wird nicht hier passieren und auch nicht (mehr) von mir gemacht werden.

Das soll reichen fuer heute. Ich møchte nur noch erwaehnen, dass erst dieses (neue) Werkzeug das (obige) Fuellhorn an Informationen zur Verfuegung gestellt hat. Das ist so’n bisschen wie damals (also ganz damals, viel frueher als mein Kevin-Bacon-damals) beim Mikroskop; die Informationen waren ja die ganze Zeit schon da, ich hab die nur (fast) nicht gesehen, weil ich die nicht „im richtigen Lichte“ betrachtet habe, weil mir bis vor Kurzem das richtige Werkzeug dazu fehlte.

Cool wa … das was eigentlich nur als Reproduzierbarkeit des ganzen Krams gedacht war hat (schon wieder) was Neues hervorgebracht. Wie ich es schon øfter erlebte, lohnt es sich sehr, am Ende nochmals auf eine Sache zu schauen mit der man sich laengere Zeit beschaeftigte. Denn dann kennt man viele der Details und wenn man das „Bild“ dann aus grøszerem Abstand anschaut, sieht man neue Sachen, die man vorher nicht sehen konnte, weil man eben diese Details noch nicht kannte. Aber ich fange an mich im Kreis zu bewegen und mache deswegen nun wirklich Schluss fuer heute.

Ohne lange Vorrede, knuepfe ich recht direkt beim letzten Mal an.
Urspruenglich schaute ich nur auf die Zitate die eine Wikipediaseite auf sich vereinte und betrachtete diese als ein Masz fuer die „Relevanz“ besagter Seite. Ich definierte (nicht formal, aber irgendwie schon) dann, dass der „Relevanzwert“ eine Art „Projektion“ der Anzahl der Zitate auf eine kontinuierliche Verteilung ist. Hier bin ich damals naeher darauf eingegangen; dennoch zur Wiederholung zwei kurze Beispiele.
– Seiten mit wenigen Zitaten werden 1:1 „projiziert“. Es gibt Seiten mit, zwei, drei, vier, oder fuenf Zitaten und deren „Relevanzwert“ entspricht dann auch 2, 3, 4 oder 5.
– Bei vielen Zitaten kommt es aber zu Luecken. Bspw. kønnte es (eine) Seite(n) mit 235 Zitaten geben, was dann (noch) einem „Relevanzwert von 235 entspricht. Wenn es nun keine Seiten mit 236 oder 237 Zitaten gibt (eine Luecke) sondern erst wieder mit 239 Zitaten, so werden Letztere einem „Relevanzwert“ von 236 (ohne Luecke!) zugeordnet.

Soweit zur Auffrischung alter Sachen. Aber eigentlich will ich vom Begriff „Relevanzwert“ weg kommen. Der Grund liegt in dem was ich beim letzten Mal schrieb: auch die Anzahl der Links die eine Seite hat ist von Interesse. Die kønnen aber nicht mehr (oder vielmehr nicht auch) als Relevanzwert angesehen werden. Dennoch møchte ich gerne zwischen Anzahl Zitaten und Anzahl Links unterscheiden kønnen.
Das oben beschriebene Prinzip hilft aus dem Dilemma heraus, denn alle Seiten welche die selbe Anzahl an Zitaten / Links haben (je nachdem, was man betrachtet) werden in eine Gruppe „geschmissen“. Und das was dann auf der jeweiligen Achse des zweidimensionalen Falschfarbenbildes abgetragen ist, entspricht der Bedeutung der Achse. Somit kommt man leicht zu den Bedeutungsgruppen, bzw. ganz konkret: Zitategruppen bzw. Linksgruppen. Am Prinzip aendert sich aber nix, nur der Name ist anders und die Interpretation bzgl. dessen fuer was besagtes Prinzip steht ist verallgemeinert worden.

An der Stelle kann ich mich um den Reproduzierbarkeitsteil des Anhangs kuemmern. Fuer die Daten von 2020 gab es nur 5,696 verschiedene Møglichkeiten wieviele Zitate eine Seite haben konnte. Weil man bei der Null anfaengt zu zaehlen (denn es gibt Seiten die keine Zitate haben), entspricht das einem høchsten Relevanzwert von 5,695. Hier ist der Vergleich mit den Daten von 2023:

Man sieht, dass sich die 2023 Daten (rote Punkte) ab ca. 3-tausend Zitaten ueber die 2020-Daten erheben. Die Vielfalt in der Anzahl der Zitate die eine Seite haben kann ist also grøszer in den neueren Daten (und damit steigt die Anzahl der Zitategruppen). Wie oben erwaehnt, werden Seiten mit wenigen Zitaten 1:1 auf die entsprechende Gruppe „projiziert“ … am Grafen kann man ablesen, dass „wenig“ bis ca. 3-tausend Zitate bedeutet.
Insgesamt gibt es in den 2023-Daten 6164 Zitategruppen, also nicht ganz 500 mehr als in den 2020-Daten.

Die S-Form hat nix zu sagen und kommt durch die halblogarithmische Darstellung zustande. Diese waehlte ich aus zwei Gruenden. Zum Einen, weil eine Seite (es ist die Hauptseite … ich frage mich uebrigens, warum die nie in den 2020-Daten auftauchte … vielleicht hat sich seitdem was in der Wikipedia an sich geaendert … oh … ich schwoffte ab) ueber 5 Millionen Zitate erhaelt und man bei linearer Abzsisse nix Relevantes sehen wuerde (nur eine Kurve die senkrecht nach oben geht und dann flach verlaeuft). Zum Zweiten, weil es bei einer logarithmischen Ordinatebei hohen Zitategruppen(zahlen?) zur „logarithmischer Komprimierung“ kommt und man dadurch auch wieder nix Relevantes (naemlich den Unterschied) sieht.

Alles in allem wuerde ich dies als reproduziert ansehen. Die Aenderung der Anzahl der Zitategruppen war zu erwarten und die Aenderung liegt jetzt nicht vøllig wild ganz woanders (bei 5 Trillionen oder so … oder auch nur ’nem Faktor 2 wenn man mal drueber nachdenkt).

Und nun kommt was Neues … und Altes was aber auch neu ist, weil ich’s vorher noch nicht gezeigt hatte: die „Projektion“ der Anzahl der Links die eine Seite haben kann auf die Linksgruppen:

Man beachte die andere Skalierung! Weil die Anzahl der Links nicht so hohe ExtremMaximalwerte hat, konnte ich beide Achsen linear belassen. Man kann aber erahnen, was ich oben mit „senkrecht nach oben und dann flach“ meine; bzw. wie nuetzlich die „logarithmische Komprimierung“ ist … aber das zog sich ja immer wieder durch diese Serie. Desweiteren sieht man eine andere, bereits erwaehnte Sache: bis ca. 1500 Links ist der Anstieg der Kurve linear und das entspricht einer (im Wesentlichen) 1:1 „Projektion“.
Ansonsten ist nur noch zu sagen, dass die Anzahl der Linksgruppen nur ca. 1/3 der Anzahl der Zitategruppen betraegt und dass besagte Anzahl auch hier (leicht) zunimmt in den 2023-Daten.
Alles in allem ist das zwar neu, aber gleichzeitig auch eine Reproduktion … toll wa! Der fruehe Wurm faengt gleich zwei Spatzen auf dem Dach :) .

Juti … das soll reichen fuer heute. Beim naechsten Mal … … … *ueberleg* … … … gibt’s dann endlich wieder bunte Bilder. Da muss ich aber noch ueberlegen, wie ich das aufziehe.

Die Dinosaurierfuszspuren vom vorletzten Mal haben mich auf die Idee gebracht, dass ich ja mal ein paar von den typischen Søren-Dingsen die ich so in Urlauben gemacht habe vorstellen kønnte.

Das beruehmteste Søren-Dingens war wohl bei meinem Besuch in den USA, vor nun bald zwei Jahrzehnten, als ich anstelle des Grand Canyon lieber zum Meteor Crater wollte. Aber die Geschichte ist ja wohlbekannt.

Es gibt eine selbstgesetzte Einschraenkung fuer diese Miniserie: es muss ein Bild vorhanden sein, wie ich vor (etwas) stehe. Die ersten Beitraege in dieser Miniserie verbleiben in Schottland (einfach, weil ich die Bilder gerade noch bei Hand habe und nicht raussuchen muss) und los geht’s mit dem Grab von David Hume:

Cool wa! So nahe zu sein, einem der bedeutensten Denker, auf dessen Ideen (und Diskussionen mit anderen groszen Denkern der damaligen Zeit) so viel unserer heutigen (westlichen) Welt basiert!

Beim letzten Mal war ich mir noch unsicher, ob ich versuche die Relevanzbetrachtungen zu reproduzieren. Ich dachte, dass man da ohnehin nix sieht. Aber dann packte mich (mal wieder) mein Ehrgeiz und es passierte etwas Aehnlichs wie bei der Simulation von Namen.
Oder vielmehr passierte viel mehr, denn ich schrieb nicht nur den entsprechenden Programmcode neu. Denn beim Neuschreiben verallgemeinerte ich auch alles und entdeckte dabei, dass die Relevanzdiskussion nur ein spezifischer Fall ist, wie die Daten auf diese Art betrachtet werden kønnen. Deswegen der Reihe nach …

… und los geht’s gleich mit dem was eigentlich betrachtetet wird.
Damals interpretierte ich die Anzahl der Zitate die eine Seite von anderen Seiten erhielt als ein Masz fuer die „Relevanz“ einer Seite. In den zweidimensionalen Falschfarbenbildern repraesentierten die Spalten der Abzsisse und auch die Reihen der Ordinate besagte Anzahl an Zitaten.
Ein Beispiel zur Veranschaulichung: man denke sich eine Seite die insgesamt 3 Zitate erhalten hat. Diese Zitate kamen von einer Seiten die selber nur einmal zitiert wurde, einer Seite mit 23 Zitaten und einer Seite mit 23517 Zitaten. Die erste Zahl entscheidet wo man auf der Abzsisse „landet“; in diesem Fall in Spalte #4 (die Zaehlung geht bei Null los, denn es gibt Seiten die keiner zitiert). Nach oben in dieser Spalte geht der Zaehler in den Zellen #2, #24 und #23518 um eins hoch, denn diese Zellen liegen in den Reihen auf der Ordinate die einem, 23 und 23517 Zitaten (welche die Seiten haben die die allererste Seite zitieren) entsprechen.
Wenn man das fuer alle Wikipediaseiten macht, dann baut sich das zweidimensionale Falschfarbenbild der Reihe nach auf. Bei manchen Zellen geht der Zaehler viele Male um eins nach oben (und die wurden damals rot im Falschfarbenbild) und bei anderen (den meisten) gar nicht (die blieben damals blau).
Oder anders: ich schaute damals wie „relevant“ die Seiten waren, die (andere) Seiten mit einem gegebenen „Relevanzwert“ zitiert haben und hier hatte ich das im Detail besprochen.

Nun ist die Anzahl der Zitate aber nur eins (von zwei) Merkmalen die eine Seite kennzeichnen. Das andere ist die Anzahl der Links.
Zur besseren (wenn auch definitiv nicht richtigen) Veranschaulichung, kønnte man sich besagte Anzahl der Links als eine Art „Recherchewert“ vorstellen. Je mehr Links eine Seite hat, um so besser ist diese recherchiert.
Dann kønnte man schauen, wie gut die Seiten recherchiert sind, die (andere) Seiten mit einem gegebenen „Relevanzwert“ zitiert haben. Man wuerde hier also die Anzahl der Links ueber der Anzahl der Zitate auftragen.
Dieses Diagramm ist aber nicht symmetrisch, denn die Relation wie die Daten zustande kommen geht nur in eine Richtung — (die auf der Ordinate abgetragenen Seiten zitieren die auf der Abszisse abgetragenen Seiten). Man kann das „Links-ueber-Zitate“-Falschfarbenbild also nicht „rueckwaerts“ lesen, wenn man wissen will wie „relevant“ die Seiten waren, die (andere) Seiten mit einem gegebenen „Recherchewert“ zitiert haben. Um das zu untersuchen muss man „Zitate-ueber-Links“-Falschfarbenbild erstellen.
Als Letztes kann man dann auch noch schauen, wie gut die Seiten recherchiert sind, die (andere) Seiten mit einem gegebenen „Recherchewert“ zitiert haben. Das entspricht einem „Links-ueber-Links“-Falschfarbenbild.

Oder anders: die „Bedeutung“ der Achse kann sich aendern, je nachdem, was darauf abgetragen ist. Das wiederum ist ein maechtiges Werkzeug, mit dem man viel ueber die Daten herausfinden kann. Damals ist mir das entgangen und ich entdeckte das erst jetzt, beim nochmals drueber nachdenken.

Nun ist das Kevin Bacon Projekt aber eigentlich abgeschlossen und ich habe auch keine Lust mehr, das alles detailliert zu untersuchen. Andererseits møchte ich besagtes Werkzeug genau besprechen.
In den naechsten paar Beitraegen wird Letzteres passieren und dabei werde ich „zweigleisig“ Diagramme und Falschfarbenbilder praesentieren. Um der Reproduzierbarkeit gerecht zu werden, werde ich Falschfarbenbilder vergleichen, bei denen die „Bedeutung“ beider Achsen der Anzahl der Zitate entspricht, die aber zum Einen aus den Daten von 2020 und zum Anderen aus den Daten von 2023 generiert wurden.
Dies wird aber nur einen (relativ kleinen) Teil ausmachen, denn ich møchte auch die Falschfarbenbilder aller anderen Achsenbedeutungskombinationen vorstellen. Auch dabei werde ich den Vergleich anfuehren, allerdings sind solche Bilder ja auch dann neu, selbst wenn sie mit Daten aus dem Jahre 2020 entstanden sind.

Bei all dem (denn das wird schon genug), werde ich nicht (nochmal) alles genau anschauen. Im Wesentlichen habe ich vor, nur besagte Falschfarbenbilder rein zu stellen als Veranschaulichung dessen, was das Werkzeug kann und ich habe vor den Fokus der Diskussion auf Letzteres zu legen.
Andererseits muss ich auch auf ein paar Dinge im „Dunstkreis“ dieses Werkzeugs eingehen. Auch hier habe ich vor 2020-Daten mit 2023-Daten zu vergleichen.

Das soll reichen fuer heute. Und weil’s systematisch vonstatten gehen soll, muss ich beim naechsten Mal zunaechst den „Relevanzwert“ nochmals genauer betrachten (und dabei zum „Bedeutungswert“ verallgemeinern).

Im Sommer ging’s nach Schottland und der Høhepunkt der Reise waren fuer mich ein typisches Søren-Dingens; naemlich Vertiefungen im Boden … auch genannt Pfuetzen. Das waren aber gar keine Pfuetzen sondern Fuszspuren von Langhalsdinosauriern! Und nicht nur irgendwelche sondern einige der weltweit am besten erhaltenen Fuszspuren … und das auch noch aus dem Mitteljura, einer Epoche der Erdgeschichte aus der wir (als Menschheit) bisher nur sehr wenige Fossilien gefunden haben.

Ich wusste, dass es Dinosaurierfuszspuren auf der Isle of Skye gibt, aber von diesen spezifischen wusste ich nix. Liegt vermutlich daran, dass an anderer Stelle welche von Theropoden zu finden sind, die mit ihren charakteristischen drei groszen Zehen nicht nur wie Pfuetzen aussehen … aber ich fand Sauropoden schon immer cooler :). Deswegen war ich sehr erfreut davon zu høren, als wir zunaechst das lokale Dinosauriermuseum besuchten.

An dem Tag waren uns die Gestirne hold, denn die Fuszspuren liegen bei Flut unter Wasser. Aber zunaechst hiesz es: suchen, suchen und nix finden. Ich wusste naemlich nur, dass die am Strand der dortigen Burgruine zu finden sind … der ist aber recht grosz. Also schaute ich mal im Internet und siehe da: es gab Berichte, sogar mit Fotos … das war fetzig, denn dadurch wusste ich wenigstens, nach was fuer Pfuetzen ich Ausschau halten muss (denn es gibt natuerlich noch viel mehr, die aber weniger spannenden Ursprungs sind). Anderweitig halfen mir diese Berichte aber nicht weiter, denn in keinem stand mehr als „geh an den Strand bei der Burgruine“ … verdammt.

Dann aber fiel mir ein, dass ich ja ’ne wissenschaftliche Ausbildung habe und dachte mir: .oO(Der Fund ist doch bestimmt in einem wissenschaftlichen Journal vorgestellt worden und da wuerde ich ’ne ordentliche Ortsangabe erwarten) … und siehe da, mit dieser Herangehensweise fand ich, dank einer Suchmaschine fuer wissenschaftliche Artikel, innerhalb kuerzester Zeit besagten Artikel. Der ist von Brusatte, S. L. et al. mit dem Titel „Sauropod dinosaur trackways in a Middle Jurassic lagoon on the Isle of Skye, Scotland„, verøffentlicht im Scottish Journal of Geology, 52 (1), 2016, pp. 1–9 … *hust*.
Wie erwartet, geben die Wissenschaftler eine nachvollziehbare Auskunft ueber die Lage …

… und schwuppdiwupp, fand ich die Pfuetzen … und stand damit an der gleichen Stelle wie’n Dinosaurier vor ca. 165 Millionen Jahren:

URST COOL, wa! Aus dem Artikel erfuhr ich dann noch, dass es sich bei dem vorbeistapfenden Urwesen wahrscheinlich um einen nicht-Neosauropoda gehandelt haben muss … also kein Brachiosaurus … der laeszt naemlich noch ca. 10 Millionen Jahre auf sich warten … sondern ein Urtier eher wie das hier:

Zby atlanticus, Quelle, Originalquelle, Autor: Nobu Tamura, Lizenz: CC BY-SA 4.0.

Mhmmmm …

… nee nee … bin ganz sicher NICHT enttaeuscht, denn dafuer sind Langhalsdinosaurier viel zu cool!

Ach ja … aus dem verlinkten Artikel lernte ich, dass solche Dinosaurier mglw. (zumindest teilweise) Wasserhabitaten zum Teil ihres Lebensraumes zaehlten. Dass die also mglw. doch (zumindest teilweise) so gelebt haben wie ganz frueher gedacht. Damals dachte man, dass das aufgrund der Grøsze so gewesen sein muss; eine Sichtweise die sich aber bereits vor ueber 50 Jahren als falsch herausstellte. Seitdem weisz man, dass es (wenn auch langsame und vermutlich wenig graziøse) an Land lebende Tiere waren.
Nun weisen die Spuren aber keine Austrocknungsmerkmale (wie Risse) auf. Die haben also IMMER unter Wasser gelegen. Auszerdem gibt es in dem Gebiet Fuszspuren in verschiedenen geologischen Ablagerungen mit laengeren zeitlichen Spruengen dazwischen.

The new prints from Skye provide interesting information on the environments inhabited by sauropods. They record multiple groups of sauropods living and moving within a marine–brackish lagoon environment. […]
Because of the sheer number of footprints, and their occurrence in three distinct stratigraphic layers, the Skye site suggests that sauropods frequented lagoon systems in Middle Jurassic Scotland, possibly over a long period of time. […]
It appears, therefore, that multiple generations of sauropod dinosaurs called the ancient lagoons of Skye home.

Aber Achtung:

Whether these sauropods merely passed through the lagoons quite frequently or were habitually resident within them is difficult to determine.

Wir sind also NICHT zurueck zur veralteten Sichtweise, dass diese wunderbaren Wesen sich im Wasser aufhalten mussten um nicht an ihrem eigenen Gewicht zu zerbrechen. Aber feuchte Umgebungen kønnten eine wichtigere Rolle als Habitat fuer solche Saurier gespielt haben, als nur als Wasserquelle.

Alles in allem ist das sowas wie die Apollosache von neulich. Auf den Mond kønnte ich zumindest theoretisch kommen, das Universum hat da prinzipiell nichts dagegen. Aber im Mitteljura Dinosaurier besuchen kann ich nicht mal theoretisch, da Universum hat da ganz prinzipiell was dagegen. Aber den Fuszspuren sei Dank, bin ich besagter Epoche und besagten urzeitlichen Tieren

[…] (im uebertragenen Sinne) nun ein gutes gigantisches Stueckchen naeher bin als die meisten Menschen … fetzt wa!

Geburtstagsbeitrag! … … … .oO(Hab ich’s doch nochmal geschafft) … … … Ihr, meine lieben Leserinnen und Leser wisst was das bedeutet … deswegen ohne weitere Umschweife: das hier ist eins der (fuer mich) allerwichtigsten Buecher welche ich jemals las:

Eigtl. hab ich es (fast) zwei Mal gelesen, denn es gehørt definitiv auch zu den allerschwersten Buechern welche mir untergekommen sind (und ich hab vor vielen Jahren zum Spasz ’n Buch ueber LASERtheorie gelesen!), weswegen ich ueber (sehr) viele Abschnitte mehrfach „gehen“ musste um die wenigstens halbwegs zu verstehen.
Davon abgesehen, dass Hannah Arendt ganz wunderbar schreibt (sprachlich, logisch, thematisch, strukturell … und sicherlich noch mehr Sachen, die extrem gute Buecher ausmachen), liegt ein groszer Reiz ihres Werkes fuer mich darin, dass sie einfach davon ausgeht, dass der Leser intelligent genug ist und ueber genuegend Hintergrundwissen verfuegt, um ihren Argumenten folgen zu kønnen … oder interessiert genug ist, um sich solche Kentnisse anzueignen. Letzteres geschah bei mir fuer wesentliche Punkte ihrer Argumentationen eher zufaellig, weil ich den „Vorgaenger“ …

… vor dem ganz oben gezeigten Buch las. Ein weiteres Buch, das zu den allerwichtigsten die ich jemals las gehørt … im Wesentlichen aus den selben, im naechsten Abschnitt naeher dargelegten Gruenden. Es sollte aber gesagt werden, dass es ist nicht wirklich der „Vorgaenger“ zu obigem Buch ist, da die Ideen aus „The Human Condition“ in „The Life of the Mind“ nicht in dem Sinne direkt (!) weiter diskutiert werden. Aber besagte Ideen sind oft grundlegend und werden auf eine Art und Weise INdirekt weiter diskutiert.

Dennoch waeren mir noch vor ein paar Jahren (insb. bevor ich anfing mehr ueber die Antike zu lesen), beide Buecher mglw. „zu viel“ gewesen … so war’s nur „80 % zu viel“ … und die restlichen (von mir halbwegs verstandenen) 20 % haben es voll krass in sich!
Vom erwaehnten wundervollen Schreibstil abgesehen schreibe ich so schwaermend, denn Sie beantwortet … oder vielmehr: Sie diskutiert (im Geiste) mit mir, viele der Themen, welche mich schon seit Jahren beschaeftigen und die sich im Wesentlichen in der mitnichten trivialen Frage „Wer bin ich?“ zusammenfassen lassen. Das hier ist der dazu gehørende „archetypische“ Beitrag den ich „immer“ verlinke (unter anderem, weil dieser auch schøn zeigt, wie lange mir das alles schon im Geiste herumgeht), aber derer gibt es viele, mehr oder weniger mit der Frage verbundene Beitraege … und bei manchen (vielen?) war ich mir beim schreiben dessen nicht mal selber bewusst … aber so ist das nun mal in der Entwicklung eines … Menschen … aber darum soll es heute nicht (schon wieder) gehen.

Kann (und will) ich die Buecher empfehlen? Oh absolut! … Aber ich haette Angst, dass ihr Hannah Arendts Werk nicht genauso groszartig und wichtig findet wie ich … und deshalb lasse ich davon ab.

Genug geschwaermt … ganz konkret geht es mir heute nicht um das ganze Universum (im solipsistischen Sinne obiger nichttrivialer Frage), sondern darum, dass sie eine Frage die ich jahrelang hatte „im Vorbeigehen“ beantwortet. Die Frage ist einfach: „Wie kann ich einen freien Willen haben, Wenn Gott (keine Diskussion diesbezueglich an dieser Stelle!) alles weisz?“. Mehrere Dekaden lang stellte ich mir vor, dass das ein „Hab dich!“ gegenueber (insb.) christlichen Glaeubigen waere. Damit einher ging ein befriedigendes Gefuehl der Ueberlegenheit … nicht wissend, dass sich das (Hannah Arendt sei Dank) nochmal gegen mich wenden soll. Besonders kurios an der ganzen Sache ist, dass ich mir die Frage schon selbst beantwortet hatte … niedergeschrieben in einem frueheren Geburtstagsbeitrag.
Nur „legte“ ich die „Teile“ nicht zum Ganzen zusammen. Oder anders: das Gefuehl der Ueberlegenheit sollte bei „den Christen“ liegen, denn Augustinus von Hippo (JA! DER!) war mir diesbezueglich mehr als 1 1/2 Jahrtausende voraus.

Aber der Reihe nach und da es mein Geburtstagsbeitrag ist, erlaube ich mir heute lange Zitate (Hurra!) aus dem ganz oben vorgestellten Buch, denn in Hannah Arendts Worten klingt das alles nicht nur viel besser, sondern ist auch viel logischer dargestellt. Die folgenden Zitate finden sich alle ab S. 104 ff., des zweiten Teils des Buches (Willing) im Kapitel mit dem Titel „Augustine, the first philosopher of the Will“.

Zunaechst stellt sie das Problem konkret (und nicht so wischiwaschi wie ich) vor:

The divine author created the world of His own free will […] [a]nd He created man after His image, that is, endowed, too, with a free will. […] Insofar as God is omnipotent (He can overrule man’s will), and has foreknowledge, human freedom seems to be doubly canceled out.

Wenn ich mich richtig erinnere, dann habe ich vor vielen Jahren (doch) mal versucht das mit ’nem Glaeuigen zu diskutieren. Aber ich hatte das Gefuehl, dass das Problem, dass sich Schicksal (und nichts anders bedeutet ein allwissender (und -maechtiger) Gott) und freier Wille, fundamental (also in JEDER unserer normalen, auf Alltagserlebnissen basierenden, Vorstellungen des Ablaufes der Zeit und wie Kausalitaet funtkioniert) ausschlieszen, wurde nicht so richtig verstanden. Hannah Arendt dazu:

The standard argument, then, is: God only foreknows; He does not compel. […]

[…] this reasoning always […] [ends] in contradictions and paradoxes.

Das von mir nur kurz erwaehnte Problem ist zeitlich zweigeteilt und Sie legt es rasiermesserscharf dar:

When you were sick, whether you would recover or not recover was predestined, hence why have called a doctor; but whether you called a doctor or did not call him was also predetermined, and so on. In other words, all your faculties become idle once you think along these lines without cheating. The reasoning relies on antecedent causes; that is, it relies on the past. But what you actually are interested in is of course the future. You want the future to be predictable–„it was to be“–but the moment you start arguing along these lines, you are up against another paradox: „If I can foresee that I am going to be killed tomorrow in an airplane crash, then I will not get out of bed tomorrow. But then I will not be so killed. But then I will not have correctly foreseen the future.“

Die Schwachstelle in der Argumentation (und der entscheidende Hinweis auf die Løsung des Paradoxons) liegt darin, dass …

[…] the first [argument] extrapolates the present into the past, the second [argument] extrapolates it into the future, and both assume that the extrapolator stands outside the sphere in which the real event takes place and that he, the outside observer, has no power at all to act–he himself is not a cause. In other words, since man is himself part and parcel of the temporal process, a being with a past […] he cannot jump out of the temporal order.

Das Argument fuer die Koexistenz eines allwissenden Gottes und des freien Willens der Menschen geht nun so (Hervorhebung von mir, Hannah Arendt zitiert hier Augustinus):

Human knowledge is of “various kinds”; men know in different ways things which as yet are not, things which are, and things which have been. [But] not in our fashion does He look forward to what is future, nor does He look at what is present nor look back at what is past, but in a manner far and profoundly different from the way of our thoughts. For He does not pass from this to that [following in thought what has changed from past to present to future], but He sees altogether unchangeably; so that all things which [for us] emerge temporally–the future which is not yet as well as the present that already is and the past which is no more–are comprehended by Him in a stable and sempiternal presence: […] [He does not see] in different fashion the now, the before, the later; for His knowledge, unlike ours, is not a knowledge of three different times, present, past, and future through whose variations our knowledge is affected. […] For He knows all times with no temporal notions, just as He moves all temporal things with no temporal movements.

Sie fasst das Argument zusammen:

In this context, one can no longer speak of God’s Foreknowledge; for Him, past and future do not exist. Eternity, understood in human terms, is an everlasting present. „If the present were always present … it would no longer be time but eternity.“ […]

[…] if one can assume that there is a person for whom the temporal order does not exist, the co-existence of God’s omniscience and man’s free will ceases to be an insoluble problem.

Oder anders: Gott ist ein mehrdimensionales Wesen … und genau so (wenn auch nicht mit diesen Worten) hatte ich im Wesentlichen im erwaehnten frueheren Geburtstagsbeitrag auch fuer eine, fuer mich unwiderlegbare (im Sinne eines starken (!) Agnostizismus), Existenz eines Gottes argumentiert.

Oder noch anders: man denke sich einen Wanderer, der sich in einer flachen (zweidimensionalen!) Ebene bewegt und pløtzlich an eine Barriere gelangt, die in die dritte Dimension reicht und unueberwindbar ist (vulgo: ein zu steiles Gebirge). Ich setze mich nun in ein Flugzeug und erlange dadurch die Møglichkeit mich in der dritten Dimension zu bewegen … eine Bewegung, die dem Wanderer nicht møglich ist. Dadurch kann ich den einen Pfad der durch besagtes Gebirge fuehrt entdecken. Ich erlange somit Wissen darueber, wie sich der Wanderer in der Zukunft bewegen wird, wenn er auf der anderen Seite der Berge ankommen will.
Dieses all zu vereinfachte Prinzip in die (mindestens) vierte Dimension erweitert fuehrt dann zur Antwort auf obige „Hab dich!“ Frage … siehe die Zitate. Wobei ich zugebe, dass ich mich da von meinem „Gefuehl“ bzgl. der Richtigkeit der (wissenschaftlichen) Verallgemeinerung fuehren lasse. Denn auch wenn die Zitat die Sache schon sehr klar machen, bekomme ich das im Detail nicht so richtig „verarbeitet“. Zeit ist fuer mich linear und vor allem NICHT „ueberschaubar“ und daran haengt mein (instinktuelles!) Verstehen des freien Willens meines „_ichs_“. Aber das waere ja nicht das erste Mal, dass die „Mathematik“ kontraintuitiv, aber dennoch (!) richtig, ist und wenn man ihr folgt, zu neuen Erkentnissen kommt … fetzt wa!

Und hier schlieszt sich der Kreis, denn nachdem ich das Zitierte gelesen hatte, konnte ich sofort die Verbindung zu meinen eigenen Gedanken diesbezueglich herstellen und war pløtzlich peinlich beruehrt. Haette ich die „Hab dich!“-Frage jemals so (insb. in Verbindung mit dem Ueberlegeneheitsgefuehl) einem schlaueren Menschen gestellt, waere dessen Reaktion so gewesen:

Und davor greuelt mir … ausgelacht zu werden (auch wenn es nur innerlich ist).

Unwissen (oder falsches Wissen) sind eine Sache. Sich aber „besser als Andere“ anzusehen (was ich ja gemacht habe), weil man sich zu fein war, oder keine Lust hatte, sich in das „Weltbild“ der Anderen hinzuversetzen und von deren Standunkt aus zu verstehen, rechtfertigt eine solche Reaktion … Pseudointellektuelle verdienen das … insbesondere (!) wenn es sich dabei um mich handelt und mich nur eine solche Reaktion dazu bringt mal laenger drueber nachzudenken, warum besagte Andere ’ne Sache so sagen wie sie die sagen.

Und da war der zweite Grund fuer den Titel dieses Geburtstagsbeitrags: die (zu meinen eigenen) orthogonalen „Weltdimensionen“ der Anderen verstehen und dadurch meine eigenen Ansichten und Argumente zu verbessern ist besser als „Hab dich!“-Fragen (oder Antworten) fuer das Ueberlegenheitsgefuehl … auch wenn (oder vllt. gerade weil?) sich Letzteres gut anfuehlt.

UND ACHTUNG: „eigene Ansichten verbessern“ heiszt NICHT, dass man die Ansichten der Anderen annimmt … Mitnichten! Das heiszt _nur_, dass man versucht sich in besagte Andere hinein zu versetzen, sich auf sie „einlaeszt“ um sie ehrlich (!) besser als Menschen, und warum sie so denken, zu verstehen.

Das soll genug sein fuer meinen diesjaehrigen Geburtstagseinrag … fein issa jeworden! Aber das Thema mit dem ich hier abschliesze werde ich anhand eines konkreten Beispiels an anderer Stelle nochmal aufgreifen.

Dieses Bild …

… zeigt eine Konstante, die uns vom vom hohen Norden bis zum tiefen Sueden des Landes der aufgehenden Sonne begleitete: die Badezimmer waren in fast allen Hotels in denen wir waren die Gleichen.

Das Arrangement der notwendigen „Badmøbel“ … ist ’ne Badewann (oder Waschbecken, oder Toilette) eigtl. ein Møbel? … ist immer das Gleiche und befindet sich in einer kompakten Plastebox die nicht ganz 2 Meter breit, ca. 1 1/2 Meter lang und vllt. 2 1/2 Meter hoch ist.

Zunaechst ist mir das gar nicht aufgefallen, dass (fast) jedes Hotel die selben Badkisten hat. Das lag mglw. daran, dass das Hotel in dem wir uns am laengsten aufhielten (Tokyo) zwar ein kleines Badezimmer hatte, aber das war keine dieser Boxen.

Aber schon in Ishinomaki (dem ersten Stop nachdem wir Tokyo verlassen hatten) tauchte diese Badschachtel auf. Ich fand das zunaechst milde interessant, dass das Badezimmer eine „Fertigpackung“ ist, zumal das Hotel auch aelter schien (mit den guten Tagen schon lange hinter sich), die Badezimmerkiste aber neuer wirkte. Mir kam der Gedanke, dass das wohl bei einer Sanierung nachgeruestet wurde. In einem solchen Fall ist es sicherlich sinnvoll, sich so’n Fertigdingens reinzubauen, anstatt sich um alle Anschluesse und dergleichen separat kuemmern zu muessen (fuer viele Zimmer).

In Sapporo und den zwei Stationen danach (Hirosaki und Kyoto) habe ich mich nicht weiter drum gekuemmert. Erst im Nachhinein erinnerte ich mich, dass die dortigen Hotels auch auf diese Art und Weise vereinheitlichte Badestuben hatten.
Ich realisierte die Standardisierung erst, als ich in Hiroshima, im kranken Zustand, nicht umhin kam, ein schønes heiszes Bad, in der all zu kurzen Badewanne, zu nehmen. Lag womøglich daran, dass ich erst da gezwungen war laengere Zeit in dem Nasskabuff zu verbringen. Aus Hiroshima ist auch das Bild.

Wenn ich mich richtig erinnere, so war nur das Bad des luxuriøsen Zimmers (auch wenn es schon deutlich bessere Zeiten gesehen hat) auf der Haseninsel keine dieser Standardkisten. Und da wir bis hinunter nach Kagoshima kamen behaupte ich jetzt einfach mal, dass sich diese Spezies ueber die komplette Insel(gruppe) ausgebreitet hat.

Das ist schon ein bisschen kurios, nicht wahr.

Als naechstes hatte ich mir damals die Histogramme bzgl. der Zitate die eine Seite erhaelt und danach bzgl. der Links die eine Seite hat angeschaut. Beim naeheren Anschauen des Histogramms bzgl. der Zitate wurde ich zum ersten Mal bewusst auf  maechtige Gesetze aufmerksam. Hier und heute vergleiche ich in diesen beiden Diagrammen …

… die angesprochenen Histogramme, gebildet mit den alten und mit den neuen Daten (man beachte die unterschiedlichen Abzsissen!). Man sieht, dass sich nix Wesentliches veraendert hat.
Bei den Zitierungen gibt es nur zwei neue Seiten, die mehr als 1 Million Zitate haben. Insb. die zweite Seite davon, mit ueber 5 Millionen Zitaten, spielt gleich nochmal eine Rolle. Bei den Links hat sich die Anzahl der Seiten mit wenigen Links etwas vermindert. Keine dieser Aenderungen wuerde ich jetzt aber derart einschaetzen, dass qualitativ, oder auch quantitativ (innerhalb gegebener Grenzen), andere Schlussfolgerungen aus den Daten zu ziehen sind.

Danach hatte ich mir den kumulativen Anteil der Seiten und Zitate / Links angeschaut (als Diagramm kuriosweise zuerst bzgl. der Links und dann nachgeliefert bzgl. der Zitate). Hier der Vergleich der alten Kurven mit den neuen Kurven diesbezueglich (man beachte wieder die unterschiedlichen Abzsissen):

Wieder kann im Wesentlichen gesagt werden, dass sich nix geaendert hat. Wie auch, denn diese Kurven folgen ja aus den obigen Histogrammen.
Im Detail geschaut scheint bzgl. der Zitate die blaue Kurve fuer grosze Werte auf der Abzsisse etwas „abzusacken“. Das ist schnell geklaert und einzig und allein durch die eine, oben erwaehnte Seite zurueckzufuehren. Diese haeuft naemlich ueber 5 Millionen Zitate nur auf sich selber an und das macht dann den „Knick und Sprung“ ganz am Ende und „schiebt“ den Rest der Kurve nacht unten. Weil’s nur eine einzige Seite ist, hat das keine Auswirkungen auf die rote Kurve und nimmt man diese Seite raus, sind die blauen Kurven beinahe deckungsgleich.
Bzgl. der Links ist die leichte „Verschiebung nach unten“ bei der neuen roten Kurve durch die gerungfuegig geringere anzahl an Seiten mit wenigen Links zu erklaeren.

Das soll reichen fuer heute :) . Ich bin mir noch nicht sicher, ob ich mir die Relevanzbetrachtungen nochmal anschaue, denn diese folgen mittelbar ja auch nur aus obigen Histogrammen. Auszerdem hatte ich da „nur“ bunte 2D-Falschfarbendarstellungen bei denen ich genau „reinzoomen“ musste um Details zu besprechen. Oder anders: bei denen sieht man bei so kleinen Veraenderungen ohnehin keinen Unterschied (und „reingezoomt“ hatte ich nur bei Anomalien die vermutlich immer noch da sind und wenn nicht mir auch nix ueber das Grosze und Ganze verraten). Solche „bunten Karten“ kann ich auch nicht zum besseren Vergleich uebereinander legen. Vermutlich werd ich da also nicht nochmal drueber schauen mit den neuen Daten … allerdings dachte ich zunaechst genau so bzgl. der Simulation von Namen … mhm mhm mhm.

AHA! Nun ist es endlich passiert … und ausgerechnet in einem dtsch. Restauraunt in Uppsala:

Tihihihihi

Es ist schon ein klein wenig laenger her, als ich den ersten Teil schrieb, in dem ich mich eher in einem „meta-Sinne“ ueber den Kommentar (in Artikellaenge) von Shizuyo Sutou in Genes and Environment, 40 (article number 26), 2018 mit dem Titel „Low-dose radiation from A-bombs elongated lifespan and reduced cancer mortality relative to un-irradiated individuals„ ausliesz.
Es waren dann erstmal andere Sachen zu tun und auch keine Lust vorhanden das hier zu schreiben. Nun sitze ich aber gerade (und noch eine Weile) im Zug und habe zwar immer noch keine Lust … aber auch nix anderes zu tun. Selbstueberredung sei dank folgt dem ersten Teil endlich mal der zweite Teil.

Zunaechst sollte ich sagen, was Hormesis ist:

Hormesis is a two-phased dose-response relationship to an environmental agent whereby low-dose amounts have a beneficial effect and high-dose amounts are either inhibitory to function or toxic.

Das ist uns (also euch, meinen lieben Leserinnen und Lesern und mir) hier im Weblog auch schon begegnet, wenn auch in „umgekehrter Form“: lange wurde angenommen, dass Alkohol „hormetisch“ ist; kein oder zu viel Alkohol sind schlecht, das „richtige“ Masz aber ist gut … der Widerlegung dieser dummen „Volksweisheit“ widmete ich eine eine eigene Miniserie und werde deswegen nicht (nochmal) naeher darauf eingehen.

Meine erste persønliche Erfahrung mit einem „hormetischen Stoff“ hatte ich in Form einer Frage die mich sehr beunruhigte. Als naemlich der junge Mann der bei mir wohnt noch nicht geboren war, sein ganz individueller Phaenotyp sich aber schon kraeftig aus dem (ebenso individuellen) Genotyp entwickelte, poppte in meinem Gehirn pløtzlich die Frage auf: .o(Ach du Schreck! Woher weisz der neue Mensch denn, dass er sofort nach der Geburt alleine atmen muss?).
Die Antwort liegt im Kohlenmonoxid. Das ist naemlich ein Neurotransmitter und wenn von dem zu viel im Blut ist (weil man bspw. nicht atmet), dann startet das „Froschgehirn“ den Atemreflex. Das heiszt also, dass dieses Molekuel in kleinen Dosen nuetzlich fuer den Kørper ist, waehrend es bekannterweise in groszen Dosen vergiftend wirkt.

Und nun endlich zu dem worueber das erwaehnte Kommentar eigtl. handelt: (sehr) (leichte) Radioaktivitaet fuehrt zu weniger Krebstoten.

Wie erwaehnt fuehrt Sutou eine Vielzahl (meiner Meinung nach durchaus plausibler) Forschungsergebnisse an, warum dem so sein sollte. Und relativ kurz nachdem ich den Artikel angefangen hatte zu lesen, definitiv noch bevor ich meine Meinung diesbezueglich modifizierte, poppte in meinem oben erwaehnten Gehirn die Idee eines Mechanismus auf, wie das sein kønnte … und der geht (ganz grob und vereinfachend) so:
– Krebszellen sind (im Wesentlichen) unsterblich, die (hier ebenso bereits thematisierte) Apoptose funktioniert nicht richtig, weil die dafuer nøtigen Gene „kaputt“ sind;
– es ist aber so, dass Apoptose auch von den Mitochondrien eingeleitet werden kann;
– wenn nun ein bisschen Strahlung die (Krebs)zelle noch ein bisschen mehr kaput macht, kønnte das gerade ausreichen, dass die Mitochondiren aktiv werden und den Zelltod einleiten, obwohl die (Zellkern)Gene dafuer ausgeschaltet sind;
– das fuehrt dann dazu, dass Krebszellen absterben, bevor sie sich massiv vermehren und zu einem Problem werden;
– gesunde Zellen werden natuerlich auch geschaedigt, aber weil die Apoptose dort richtig funktioniert sterben die einfach nur ab und es macht fuer den Gesamtorganismus keinen Unterschied ob das nun wegen wenig Strahlung oder wegen was anderem war;
– das Ganze ist natuerlich ein Prozess der selber auch zu Krebs fuehren kann, wenn die Strahlung ueberhaupt erste besagte „Apoptosegene“ kaputt macht;
– aber es gibt urst URST viel DNA-„Material“ was scheinbar (anscheinend?) ueberhaupt keine Funktion hat (also bspw. (und meistens) nicht in Eiweisze ausgedrueckt wird) und Strahlung „trifft“ auf die DNA rein statistisch und bei geringer Strahlung ist es wahrscheinlicher, dass ein Bereich der DNA getroffen wird, bei dem das nicht so schlimm ist und unwahrscheinlich, dass ein „Apoptosegen“ beschaedigt wird;
– nun ist die Zelle aber groeszer als der Zellkern und es kønnte sein, dass (geringe) Strahlung in ihr rein statistisch gesehen etwas haeufiger ’ne Sache kaputt macht, die dann die Mitochondiren alarmiert und manchmal ist das dann ’ne Krebszelle;
– das Ganze hørt bei Strahlungsdosen die nicht mehr als gering (!) bezeichnet werden kønnen auf zu funktionieren, einfach weil die Chance „gute DNA“ zu „treffen“ (und damit zu veraendern) sich vergrøszert, waehrend (mglw.?) die Chance „irgendwas in der Zelle kaputt machen“ nicht im gleichen Masze zu nimmt;
– so weit so gut  … nun ist es auch so, dass die Erde (viel) frueher etwas mehr radioaktiv war, als sie es heute ist … es wuerde mich also nicht wundern, wenn damals die ersten DNA enthaltenden Organismen sich so entwickelten, dass es insgesamt von Vorteil war mehr „unnuetze DNA“ mit sich „rumzuschleppen“ um etwas bestaendiger gegen besagte Strahlung zu sein;
– damals fuehrte das zwar zu weniger mutierten Zellen, aber weil das so frueh in der Evolution entstanden ist, ist es so sehr in den „Funktionsprinzipien der DNA“ (und damit des ganz allgemeinen Lebens) eingebaut und deswegen ist das immer und ueberall sowieso da und zaehlt somit nicht wirklich zum besagten Mechanismus sondern ist eher eine Art „evolutionaer verminderte Krebsbasisrate“;
– die Mitochondiren kamen spaeter dann dazu und uebernahmen eine wichtige Rolle bei der Apoptose … dazu gehørt Zeichen zu erkennen wann eine Zelle beschaedigt ist … Letzteres ist das was (geringe) Strahlung macht;
– und ich merke gerade, dass ich anfange immer nur ueber die gleichen Sachen zu reden, nur von anderen Blickwinkeln gesehen.

Lange Rede kurzer Sinn: ich konnte es mir das also durchaus vorstellen, dass geringe Strahlung die Krebsraten (leicht!) vermindert. Sutou bringt dann im Artikel auch selbst das Argument der erhøhten Strahlung auf der juengeren Erde und dass es sinnvoll ist anzunehmen, dass die Evolution dafuer sorgte, dass uns das nicht uebermaeszig kaputt macht.

Dass ich die Idee dann selber hatte, half vermutlich unterbewusst, dass es mir leichter viel auch den Rest der Ergebnisse (nach genauem Anschauen und etwas drueber Nachdenken) zu akzeptieren und letztlich meine Meinung wesentlich zu aendern.

Und nun ist der Beitrag schon wieder so lang. Eine Sache fehlt aber noch und die handelt darueber, warum das zwar (vermutlich) alles richtig ist, ich damit aber abseits der wissenschafltich (im Uebrigen hochinteressanten) Diskussion dennoch ein Problem habe. Oder anders: Fortsetzung folgt.