Nach dem letzten Beitrag kann ich heute ohne viel Aufhebens gleich zu den Daten kommen:
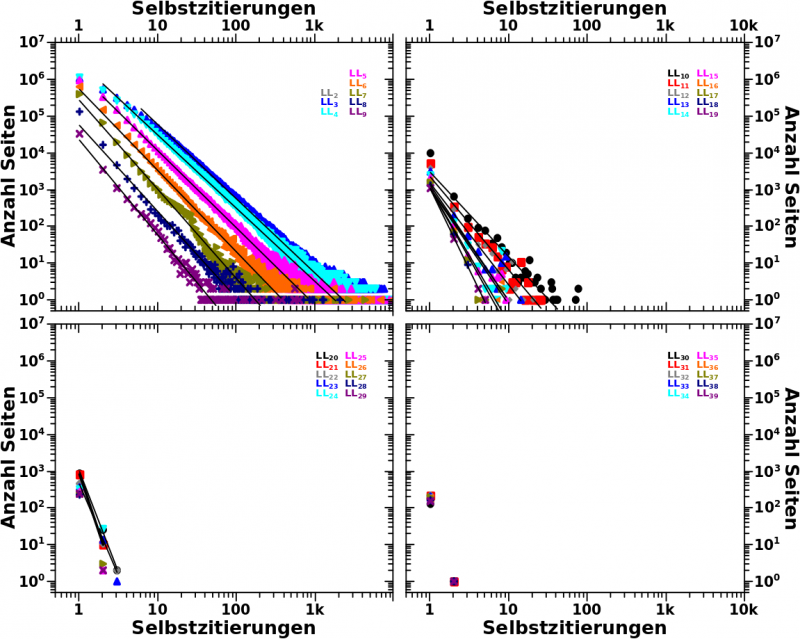
Whoa! … (wie so oft) passiert ja ganz schøn viel hier … darum der Reihe nach. Wir sehen die selben Diagramme wie beim letzten Mal, nur fuer høhere Linklevel, mit den Regressionsgeraden welche den linearen Teil der jeweiligen, linklevelspezifischen Daten gut (genug) beschreiben.
Im linken, oberen Bild sehen wir die Daten fuer LL2 bis LL9 (kurze Anmerkung: die Daten fuer LL2 und LL3 sind sich so aehnlich, dass sich Erstere hinter Letzteren „verstecken“; entsprechend sind diese zwei Regressionsgeraden auch so aehnlich, dass ich hier sage, dass diese gleich sind). Wie beim letzten Mal bereits erwaehnt, nimmt die „Signalstaerke“ mit zunehmendem Linklevel ab. Das ist aber etwas, was wir schon aus dem allerersten Diagramm zu den Selbstreferenzen wissen.
Nichtsdestotrotz scheinen die Regressionsgeraden hier alle parallel zu liegen. Die Betonung liegt auf „scheinen“, denn dies ist nicht der Fall. Das sieht man aber in diesem Diagramm nicht so gut, weil der Unterschied in den Anstiegen nicht sehr grosz ist.
Besser ist dies im rechten oberen Bild zu sehen, in dem die Daten von LL10 bis LL19 dargestellt sind. Weil die Datenpunkte dichter beisammen liegen erkennt man viel besser, dass Betrag des Anstiegs der Regressionsgeraden zu nimmt mit høheren Linkleveln.
Im linken unteren Bild sieht man den Uebergang in das Regime in dem die Datenlage nicht mehr gut genug ist. Bis LL22 getraue ich mich noch die Daten mittels linearer Regressions zu analysieren. Danach ginge das prinzipiell auch noch, aber da habe ich dann allermeistens nur noch zwei Datenpunkte (oder noch spaeter nur noch einen) pro Linklevel und durch zwei Punkte kann man eine eindeutige Gerade legen. Die Parameter dieser Gerade sind dann aber auch komplett abhaengig von der Position besagter Punkte im Diagramm. Da ich mich hier ohnehin nur noch kurz ueber dem „Rauschen“ befinde wuerden besagte Parameter dann auch (mehr oder weniger) wild streuen und es waere wenig sinnvoll diese zu interpretieren. Eben dieses „wilde streuen“ wird ja zum Teil massiv „geglaettet“ durch lineare Regression.
Wieauchimmer, im rechten unteren Bild ist dann definitiv der „Endzustand“ erreicht, der das eben Beschriebene eindeutig klar macht.
Ich zeige die Diagramme vor allem aus Transparenzgruenden damit ihr, meine lieben Leserinnen und Leser, sieht wie das „in Echt“ aussieht und wo die beim naechsten Mal besprochenen Sachen eigtl. herkommen.
Zum Abschluss sei das Folgende gesagt (denn es ist wichtig zum Verstaendnis der Daten beim naechsten Mal): wenn die Werte der Datenpunkte der Grafen durch die Anzahl aller Wikipediaseiten geteilt wird, so erhaelt man die Wahrscheinlichkeit wie oft eine Seite so und so viele Zitate (z.b. 23) pro Linklevel erhaelt.
Das Integral ueber alle derart normierten Daten und alle Linklevel ergibt die rechte Kurve des ganz am Anfang der Besprechung der Selbstreferenzen gezeigten Bildes — die durchschnittliche Wahrscheinlichkeit ueberhaupt eine Selbstreferenz zu erhalten.
Beim naechsten Mal komme ich zum eigentlich Spannenden: der nun schon so oft erwaehnten Regressionsgeraden. Urspruenglich war das hier mit drin, aber die Ergebnisse sind so toll, dass diese einen eigenenBeitrag verdient haben.
Leave a Reply