Die beim letzten Mal reproduzierten Untersuchungen fuehrten mich damals zu einem der wichtigsten Kevin Bacon Resultate ueberhaupt: die durchschnittliche Anzahl der Zitate unterliegt einem maechtigen Gesetz. Oder anders: das ist bei doppellogarithmischen Achsen linear! Krass wa!
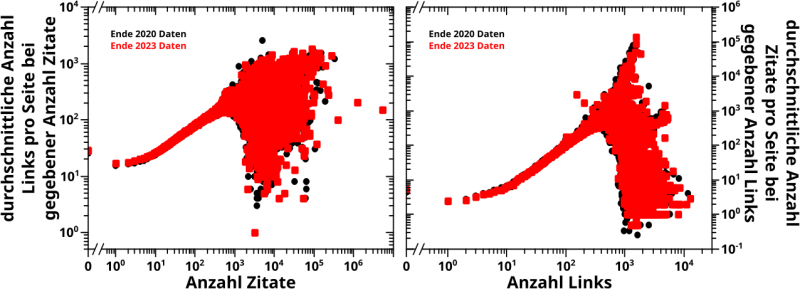
Wichtig: bei diesen Untersuchungen wurde davon ausgegangen, dass die Anzahl der Zitate die UNabhaengige Grøsze ist. Oder anders an einem Beispiel: alle Links einer Seite mit 5 Zitaten hab ich genommen und auf einen „Haufen“ geworfen. Auf diesen Haufen kamen NUR die Links von Seiten mit 5 Zitaten (egal wieviele Links das waren). Auf einem anderen Haufen haeufte ich alle Links aller Seiten mit 6 Zitaten an; usw. Fuer den Durchschnitt teilte ich am Ende einfach die Anzahl aller Links in einem gegebenen Haufen mit der Anzahl aller Seiten die zu diesem Haufen beigetragen haben.
Ich habe das nochmal so ausfuehrlich beschrieben, damit sichtbar wird, dass ich damals auch hier wieder NICHT die umgedrehte Konstellation betrachtet habe. Oder anders: wird das das Gleiche, wenn man die Anzahl der Zitate einer Seite durchschnittifiziert, wenn man die Anzahl der Links der besagten Seite als unabhaengige Grøsze hernimmt?
Tja … und hier sieht man nun beide Sachen:
Tada! Das ist auf den ersten Blick nicht das Gleiche … aber ich kann euch, meinen lieben Leserinnen und Lesern versichern, dass es sehr wohl das Gleiche ist.
Am wichtigsten ist, dass die Anstiege der linearen Teile der Daten im Groszen und Ganzen uebereinstimmen. Aufgrund unterschiedlicher Skalen sieht man das nur nicht so gut. Aber wenn man das gleich skaliert dann ist’s im Wesentlichen das gleiche Ergebniss … ich hab das jetzt zwar nicht konkret ausgerechnet, aber ich hab ’n Lineal an’n Monitor gehalten und parallel verschoben (bei richtiger Achsenskalierung) und das war im Wesentlichen das gleiche … OKOK … es war kein Lineal und Parallelverschiebung, sondern ’n Blatt Papier an den Monitor gehalten, dann hab ich (MIT LINEAL) den einen Anstieg „durchgepaust“, das Papier an der Unterkante des Monitors zum naechsten Graphen (parallel)verschoben, dort den Anstieg abgepaust … und das hatte zwar kleine Abweichungen, aber innerhalb der Genauigkeit aller Untersuchungen (und insb. der „Pausmethode“) wuerd ich sagen, dass das alles gleich war.
Und das SOLLTE auch so sein (was der Grund ist, warum das so wichtig ist), dass die Anstiege gleich sind. Auch wenn das in den beiden Faellen aus anderen Gegebenheiten so ist, denn die Anzahl der Seiten mit einem gegebenen Zitatewert ist unabhaengig von der Anzahl der Seiten mit dem selben LINKwert. Aber im Mittel ueber (sehr) viele Seiten, sollte das das Gleiche sein.
Dass dem wirklich so ist fetzt und bestaetigt im Nachhinein, dass mein Ansatz mit dem Mittelwert gar nicht so falsch ist … das ist wichtig, denn darauf basierten ein paar Schlussfolgerungen und Erklaerungen im weiteren Verlauf des Kevin Bacon Projekts.
Warum das auf den ersten Blick so ungleich aussieht, ist das unterschiedliche Verhalten des Verlaufs der beiden Durchschnitte bei hohen Werten auf der Abszisse. Was natuerlich nicht weiter verwunderlich ist, eben wg. besagter Unabhaengigkeit und weil wir hier in den Bereich kommen, wo oft nur sehr wenige, in vielen Faellen einzelne, Seiten einen ganzen Datenpunkt ausmachen … da kann man also mittels einer Durchschnittifizierung keine „versteckte“ Information „rauskitzeln“.
Ach ja, es ist eine reine Formalitaet (denn man sieht’s ja), aber ich sollte erwaehnen, dass die 2023 Daten die 2020 Daten reproduzieren.
Sooo … das ging schøn schnell heute.
Damals hatte ich dann nur noch den Rest der Verteilung der totalen Links angeschaut und da war nix weiter zu holen und ich hatte die gesamten Verteilungen bereits reproduziert. Und dann folgte (wie so oft) eine kurze Betrachtung der „Ausreiszer“, die ich hier auch nicht wiederholen werde. Dito, bzgl. der daran anschlieszenden Fehlerbetrachtungen.
Tjoa … jetzt muss ich ueberlegen ob ich mir erstmal die Linklevelverteilungen fuer die anderen drei Grøszen von Interesse anschaue (und damit dem damaligen „Spielplan“ vorgreife), oder „chronologisch“ weitermache.
Ich tendiere zu Ersterem, aber das muss ich nicht jetzt entscheiden.
Leave a Reply