Søren in Norwegen

Beim letzten Mal zeigte ich (unzureichend vereinfachend und zusammenfassend), dass Seiten mit wenigen Links im Durchschnitt laenger brauchen um zu einer beliebigen anderen Wikipediaseite zu gelangen als Seiten mit vielen Links. Unter Beruecksichtigung der „umgedrehten Situation“ gilt i.A. das Gleiche fuer Seiten mit vielen Zitaten.
Dafuer hatte ich alle Wikipediaseiten (paarweise) in Untergruppen eingeteilt und mir das Verhalten eben jener genauer angeschaut. Besagtes Verhalten ist wie erwartet, zeigt aber kleinere Abweichungen (und mindestens eine grøszere) die ich beim letzten Mal erwaehnte aber nicht weiter untersuchte (oder erklaerte).
Ebenso liesz ich (mit Absicht) einen wichtigen Vergleich weg, denn ich zeigte nicht, inwiefern die Resultate fuer die beiden „Richtungen“, aus denen das Verhalten des kumulativen Anteils der neuen Links bzw. der Linkfrequenz betrachtet werden muss, uebereinstimmen. Ueber alle Seiten betrachtet sind die entsprechenden Kurven (beinahe) deckungslgleich (und sollten es auch sein) … zumindest fuer die fruehen Linklevel bei denen „Mehrfachsichtungen“ in der Linkfrequenz noch (sehr) selten vorkommen und eben diese damit fuer einen solchen Vergleich noch nicht unbrauchbar gemacht haben.

Beide Sachen hole ich heute und beim naechsten Mal nach. Ich teile das auf zwei Artikel auf, denn ich beschraenke mich fuer diesen Artikel nur auf die Resultate fuer die Untergruppen mit wenigen Links bzw. Zitaten. Dies deswegen, weil ich zur Diskussion der Unterschiede (mal wieder) Verteilungen heranziehen muss, diese aber nicht auf die uebliche Art und Weise darstellen kann. Damit es dadurch nicht zu Verwirrungen kommt muss das genau diskutiert. Das macht den heutigen Artikel recht land und deswegen trenne ich das auf.

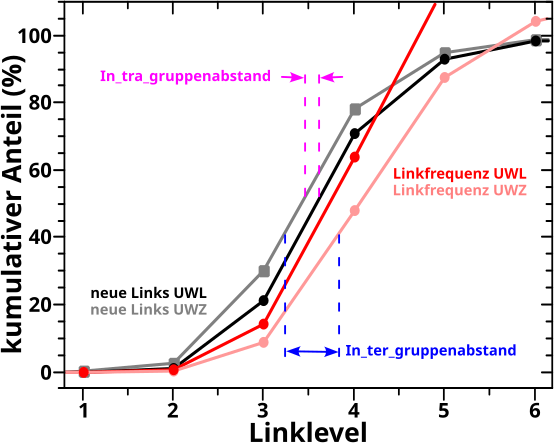
Aber nun Butter bei die Fische! Der Vergleich der kumulativen Kurven fuer die beiden „Richtungen“ fuer die Untergruppen mit wenigen Links (UWL) und wenigen Zitaten (UWZ):

AHA! Im Gegensatz zu dem was ich oben schrieb bzgl. aller Seiten, sind die Kurven hier definitv nicht (beinahe) deckungsgleich; nicht mal bis LL₃! Ist ja interessant und daraus folgt, dass zwei Unterschiede in den Kurven erklaert werden muessen: 1. der Intragruppenabstand zwischen zwei Kurven die zu einer „Richtung“ gehøren und 2. der Intergruppenabstand zwischen den Kurven der zwei verschiedenen „Richtungen“.

Dafuer muessen wir zurueck zu den Verteilungen der Links und  Zitate gehen. Natuerlich nicht fuer alle Seiten sondern nur fuer die, die sich in den beiden Untergruppen befinden.
Hier tut sich nun aber ein Problem auf mit Hinblick auf die Unterguppen mit den vielen Links / Zitaten. Diese enthalten naemlich nur wenige Seiten. Die entsprechenden Verteilung bspw. fuer die UVZ waeren dann nur 703 Striche die alle nur bis eins gehen. Auszerdem erfahren diese Striche auch noch „logarithmische Komprimierung“ und „verschmieren ineinander“.

Das ist zunaechst nix Schlimmes, denn fuer Histogramme fasst man oft ohnehin alle Messungen mit Werten (einer bestimmten Charakteristik, hier bspw. der Anzahl der Links) die nahe beisammen liegen in einem „Eimer“ zusammen. Alle „Eimer“ sind gleich grosz (bspw. 1 bis 5 Links, 6 bis 10 Links usw.)  und das Histogramm selber zaehlt fuer jeden Balken dann wie viele Messungen in dem „Eimer“ sind.
Die Wahl der Grøsze dieser „Eimer“ kann mitunter trickreich sein. Bisher brauchte ich das nicht machen, weil es so viele Wikipediaseiten gibt und die entsprechenden Verteilungen auch ohne „Eimer“ aussagekraeftig waren. Bei nur (bspw.) 703 Seiten ist dem aber nicht mehr so.

Die „Eimer“ løsen das erste Problem, die Balken der Verteilung wuerden bei gut gewaehlter „Eimergrøsze“ unterschiedlich grosz ausfallen. Nun ist es aber so, dass die Abzsisse fuer die Histogramme (wie so oft) logarithmisch ist. Wenn man nicht gerade gigantische „Eimergrøszen“ heran zieht, tritt also weiterhin das Problem der „logarithmischen Komprimierung“ auf. Ganz davon abgesehen, dass wenn „Eimer“ fuer hohe Grøszenordnungen gewaehlt werden (bspw. von 100-tausend bis 110-tausend) die gleiche „Eimergrøsze“ sich ueber mehrere Grøszenordnungen bei kleinen Werten erstreckt (in diesem Fall vier von 1 bis 10k).
Die von mir gewaehlte Løsung besteht darin, dass ich die Grøsze der Eimer davon abhaengig mache, in welcher Grøszenordnung sie sich auf der Abzisse befinden. Ich nenne das „magnitudal bins“ oder „Grøszenordnungseimer“.

Das hørt sich vermutlich komplizierter an, als es ist. Kurzgesagt teile ich jede Grøszenordnung (also von 0 … 9, 10 … 99, 100 … 999 usw.) auf der Abzsisse in neun, jeweils gleich grosze „Eimer“  ein. In der ersten Grøszenordnung „fallen“ die Seiten in jeden „Eimer“ wie gehabt. In der zweiten Grøszenordnung „fallen“ in den ersten „Eimer“ alle Seiten die zehn oder mehr Links / Zitate haben, aber weniger als 20. Der zweite „Eimer“ ist entsprechend fuer alle Seiten mit 20 bis 29 Links / Zitaten und der neunte fuer alle Seiten mit 90 bis 99 Links / Zitate. Bei 100 erfolgt der Uebergang zur naechsten Grøszenordnung und der entsprechende erste „Eimer“ ist nun zehn Mal so grosz — also eine Grøszenordnung mehr — (denn dieser enthaelt alle Seiten mit 100 bis 199 Links / Zitaten).

Das løst alle Probleme fuehrt aber zu einer kleinen Verkomplizierung, die man im Hinterkopf behalten muss. Beim Uebergang von einer Grøszenordnung zur naechsten wachsen die Balken des Histogramms pløtzlich sprunghaft an. Der Grund liegt natuerlich darin, weil in besagten Balken pløtzlich zehn Mal mehr Seiten stecken als noch einen „Schritt“ vorher. Gedanklich muss man die Balken an solchen Grenzen also entsprechend verkleinern.
Im hiesigen Zusammenhang spielt das keine all zu grosze Rolle, denn es reicht zu sehen, ob eine Untergruppe mehr Seiten links (oder rechts) vom „Maximum“ der Verteilung der anderen Untergruppe hat. Letzteres ist auch der Grund, weswegen ich die Histogramme normiere.

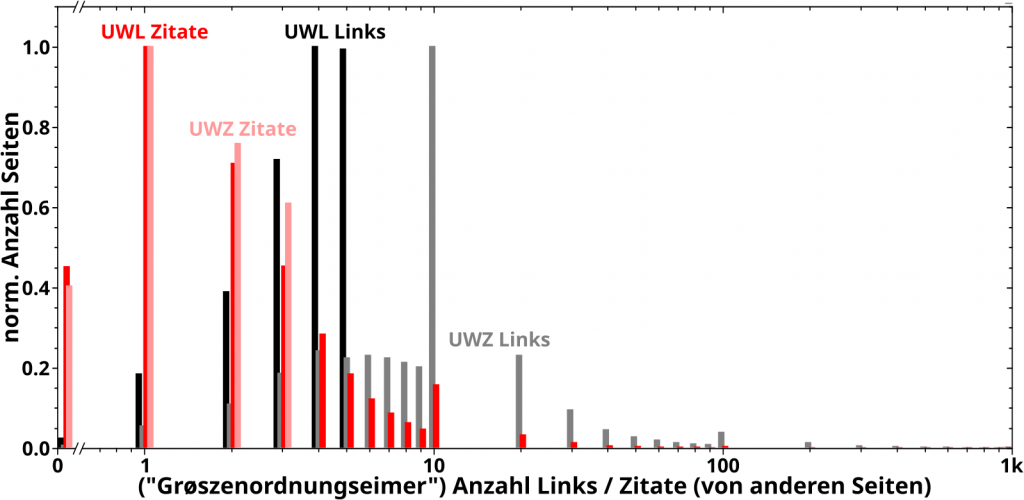
Genug geredet, hier sind sie, die Verteilungen der Links und Zitate der UWL und UWZ:

Fetzt wa! Bei den grauen Balken (Verteilung der Links der UWZ) sieht man beim Wert 10 auf der Abzsisse deutlich das Phaenomen, was man im Hinterkopf behalten muss. Nicht ganz so deutlich sieht man es auch an dem entsprechenden roten Balken (Verteilung der Zitate der UWL). Aber eigentlich will ich damit ja die Intra- und Intergruppenabstaende erklaeren. Darum der Reihe nach.
Ach so, ich hab die Abzsisse bei 1000 abgeschnitten. Danach gibt es zwar noch ein paar Balken, die sind aber so klein, dass sie vøllig irrelevant sind.

Zunaechst der Intragruppenabstand. Die Kurve fuer den kumulativen Anteil der neuen Links der UWZ (schwarz) liegt unter der Kurve fuer die UWL (hellschwarz … vulgo: grau). Das geht natuerlich nur, wenn die Seiten in der UWZ mehr (neue) Links sehen als die Seiten in der UWL. An den Histogrammen sehen wir, dass dem tatsaechlich so ist.
Ist ja auch eigentlich auch ganz klar, denn die Seiten der UWL wurden deswegen in die UWL einsortiert, weil diese 5 Links oder weniger hatten. Deswegen gibt es im Histogramm keine schwarzen Balken bei Werten mit 6 oder mehr auf der Abzsisse.
Das spielte aber bei den Seiten in der UWZ ueberhaupt keine Rolle, denn diese wurden nach der Anzahl der Zitate (0 bis 3) ausgesucht. Deswegen sind die grauen Balken ueberall zu finden und das ist entscheidend fuer den Intragruppenabstand.

Weil die UWZ Seiten (als Ensemble) signifikant viel mehr Seiten schon „ab Start“ (also LL₀) sehen (das ist was obiges Histogramm u.a. aussagt), verzweigt das Linknetzwerk auf kleinen Linkleveln schneller und somit ist die kumulative Kurve bzgl. der neuen Links der UWZ ueber der entsprechenden Kurve der UWL. Das macht auch nix, dass die beiden Untergruppen unterschiedlich viele Seiten enthalten, denn die kumulativen Kurven sind ja „normiert“.

Beim Intergruppenabstandes der kumulativen Kurven bzgl. der Linkfrequenz (die rote / hellrote Kurve(n)) geht die Argumentation genau so. Die Seiten der UWZ wurden danach ausgewaehlt, dass sie 3 oder weniger Links haben (deswegen keine rosa Balken rechts davon). Fuer die Seiten der UWL war das aber kein Kriterium und im Histogramm sehen wir an den roten Balken, dass diese von mehr Seiten gesehen werden, weswegen die entsprechende kumulative Kurve der UWL høher liegt als die der UWZ.

Nun zum Intergruppenabstand. Dafuer betrachte ich nur die hellrote und die graue Kurve (eigtl. muessten alle vier Kombinationen von (hell)rot zu (hell)schwarz untersucht werden, aber das ist immer das selbe Prinzip und gibt keinen weiteren Erkenntnissgewinn).

Die hellrote Kurve entsteht dadurch, dass die Seiten der UWZ (neue) Links sehen. Die graue Kurve entsteht dadurch, dass die Seiten der UWZ von anderen Seiten zitiert werden. Im Histogramm muessen fuer den Intergruppenabstand also die Balken der Links und der Zitate der UWZ verglichen werden. Man sieht nun, dass die UWZ sehr viele graue Balken rechts von den hellroten Balken hat. Die weitere Argumentation ist dann wie Oben.

Fuer die schwarze und rote kumulative Kurve(n) ist die Argumentation qualitativ die selbe. Quantitativ muss man aber im Histogramm etwas genauer hinschauen, denn die roten Balken erstrecken sich auch rechts von den schwarzen Balken (obwohl die schwarze Kurve ueber der roten liegt). In diesem Fall sieht man aber, dass der grøszte rote Balken definitiv links vom grøszten schwarzen Balken liegt und die roten Balken rechts vom letzten schwarzen Balken sind nicht sehr hoch. All das bedeutet, dass im Durchschnitt die Seiten der UWL NICHT von mehr Seiten gesehen werden als sie (neue) Links haben. Die zwei høchsten roten Balken sagen aus, dass die meisten Seiten nur ein bzw. zwei  Mal zitiert werden, waehrend die zwei høchsten schwarzen Balken aussagen, dass viele (mglw. gar die allermeisten) der selben Seiten mindestens vier oder fuenf Links haben. Die wenigen Seiten mit mehr als fuenf Zitaten spielen da dann auch keine Rolle mehr.

Jut … das soll reichen hierzu. Beim naechsten Mal das Gleiche fuer die anderen beiden Untergruppen und mit der ganzen Vorrede hier kann ich die Diskussion dort kuerzer halten :)