Søren in Norwegen

Bei den linklevelabhaengigen Verteilungen der totalen Links hatten wir einen Fall, bei dem die „integrierten log-log-Plots“ nicht so „funktioniert“ haben wie ich das bei allen anderen Beispielen gesehen habe. Aber das war erwartet, weil schon bei den urspruenglichen Untersuchungen nix rum kam. Im Allgemeinen konnte man sehen, dass dieser Ansatz zu mehr oder weniger guten Geraden fuehrt und (mit sinnvollen Abstrichen) haut das schon ganz gut hin.

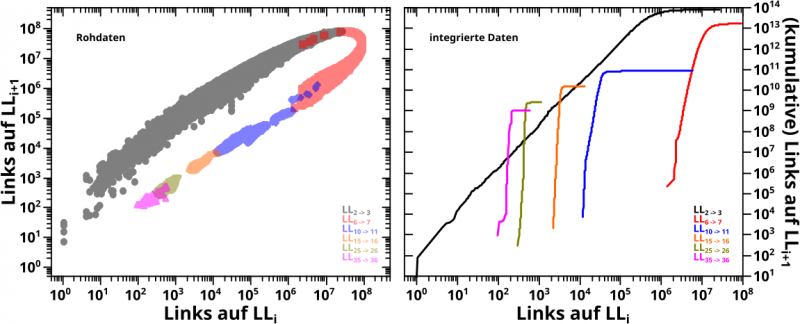
Ein unerwartetes, im Wesentlichen nichts hergebendes Ergebniss erhaelt man mit dieser Methode, wenn man sich die Links auf LL_i+1 in Abhaengigkeit von den Links auf LL_i anschaut:

Im linken Diagramm sind, wieder in blassen Farben, die urspruenglichen (Roh)Daten und die wichtige (und ueberraschende) Information war hier, dass diese einen „Orbit“ beschreiben … DAS sieht man nun ueberhaupt nicht bei den integrierten Daten im rechten Diagramm.
Zunaechst kønnte man das ja mglw. darauf schieben, dass ja NUR die Ordinate integriert ist, aber mglw. muesste man das auch fuer die Abzsisse machen. Da tritt man dann zwar in ein „konzeptuelles Wespennest“, aber das hat mich nicht davon abgehalten mich damit mal ein paar Stunden zu beschaeftigen … das Resultat: das ist zwar anders als im rechten Diagramm, ist diesem aber aehnlich und hat auch keinen „Orbit“ zur Folge.
Auf den ersten Blick sieht es auch so aus, dass man hier nicht mal die Anstiege aus den Integralen richtig raus bekommt (aus dem Bereich vor den jeweiligen Plateaus). Wobei das aber hier bei den (totalen) Links vermutlich letztlich auch wieder nur daraus folgt, was ich zum ganz zuerst verlinkten Thema schrieb … das gehørt schlieszlich zusammen.

Interessant ist, dass das was ich hier im rechten Diagramm zeige, (mit Abstrichen) bei den Selbstzitierungen funktioniert. Das war so wenig ueberraschend, dass ich dazu beim letzten Mal nicht mal ein Bild zeigte und das in drei Saetzen schnell abhandelte.
Wenn man mal drueber nachdenkt, dann ist das aber nicht weiter verwunderlich, denn die Selbstreferenzen sind nicht von sich selber, sondern von der Anzahl der (totalen) Links abhaengig. Bei Selbigen hingegen ist die Anzahl direkt von sich selbst abhaengig … ach das ist alles kompliziert und vermutlich hat das auch gar nix miteinander zu tun … was einer der Gruende ist, warum ich das oben als „konzeptuelles Wespennest“ darstelle … jemand der schlauer ist als ich, kann das mathematisch sicherlich alles herleiten, ich will mir aber darueber nicht weiter den Kopf zerbrechen

Lange Rede kurzer Sinn: hier bringt der „Integralansatz“ nix.

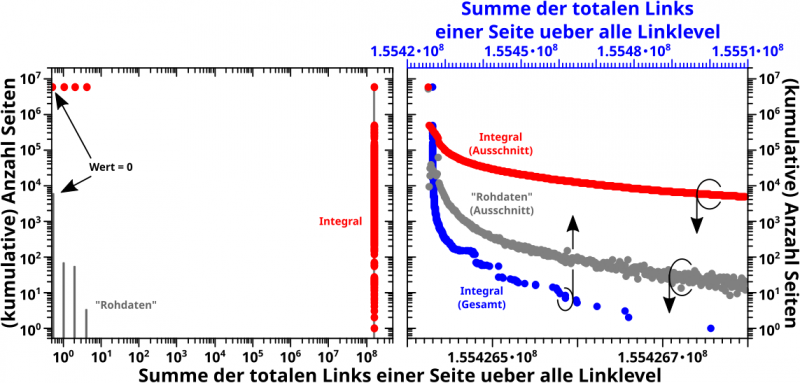
Dann war da noch die Summe der totalen Links einer Seite ueber alle Linklevel:

Achtung: im rechten Diagramm ist die untere Abzsisse fuer die grauen und roten Daten und zeigt nur einen Ausschnitt der gesamten (integrierten) Daten (blaue Punkte). Fuer Letztere gilt die obere, blaue Abzsisse.
Und JA, auch im rechten Diagramm sind die Abzsissen logarithmisch. Hier draengt sich aber alles so sehr zusammen, dass das irrelevant ist.

Ich muss hier nicht viele weitere Worte drueber verlieren, denn es ist ziemlich eindeutig, dass hier auch mit dem „Integralansatz“ nix zu holen ist. Das gilt auch dann, wenn man die Grenzen des Integrals invertiert oder die ersten vier (dominierenden) Datenpunkte weg laeszt bei den Betrachtungen (ich hab’s naemlich versucht).

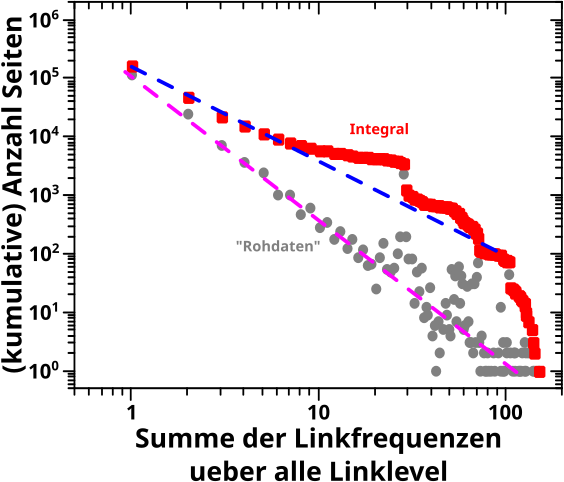
Als naechstes war da die Summe der Linkfrequenzen ueber alle Linklevel, von dem nur der „Archipelteil“ interessant war:

Das sieht ja erstmal knorke aus, ABER hier muss man vorsichtig sein … der Reihe nach.

Die gestrichelten Geraden sind wieder von Hand reingelegt und die Anstiege sind ca. 2.25 fuer die Rohdaten und ca. 1.125 fuer die integrierten Daten. Das haut also ganz gut hin.
Aufgrund von Diskrepanzen zwischen realen Daten und reiner Mathematik fallen die integrierten Daten bei Summenwerten von ueber 100 so stark ab. Wie schon vormals (nicht im Detail) diskutiert, liesze sich das „reparieren“ und dann liegen die auch auf der (gestrichelten, blauen) Gerade. Das ist also nur ein kleinerer Grund fuer die Vorsicht
Wichtiger ist, dass die „Huegel“ in den Rohdaten (auf der Abzsisse bei Werten von ca. 25 und 50) zu deutlichen Abweichungen von der Regressionsgeraden im integrierten Signal fuehren. Auch vormals gab es Abweichungen von der Geraden, aber waren das dann „glatte“ Kurven mit mehr oder weniger starker Kruemmung und ich meinte dann, dass man die Abweichungen parametrisieren (a.k.a. wegdiskutieren“ kønnte).

Lange Rede kurzer Sinn: der „Integralansatz“ ist zwar durchaus … ich sag jetzt mal: erfolgreich. Aber wenn man das genau macht, dann darf man bei solchen Faellen die (abrupten und signifikaten) Abweichungen vom Erwartungsbild nicht einfach in einen „Parameter“ packen, sondern muss das ordentlich betrachten und diskutieren … was ich hier nicht mache, weil ich keine Lust mehr habe.

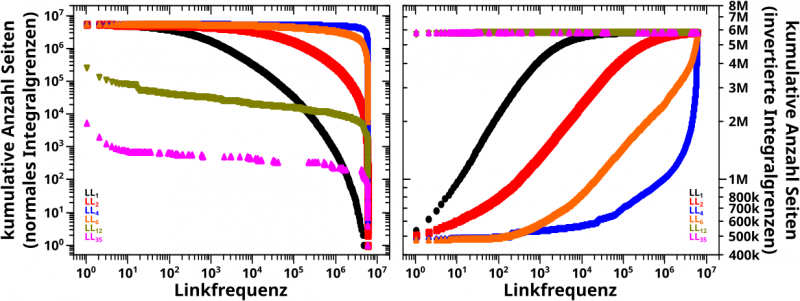
Als Letztes dann noch ein paar Beispiele fuer die linklevelabhaengigen Histogramme bzgl. der Linkfrequenz pro Seite:

Zu meiner Ueberraschung ist hier (auf den ersten Blick) nuescht linear; weder bei normalen (linkes Diagramm) noch bei invertierten Grenzen (rechtes Diagramm) des Integrals.
Naja, bei invertierten Integralgrenzen gibt es zumindest fuer die ersten paar Linklevel mglw. lineare Teilbereiche, aber viel ist da nicht „zu holen“.
Auszerdem ist die Dynamik  im rechten Diagramm echt klein; die zugehørige Ordinate geht gerade mal ueber ein bisschen mehr als eine Grøszenordnung.
Lange Rede kurzer Sinn: der „Integralansatz“ kann hier vllt. ein paar Resultate liefern, die kønnen aber nicht auf den ganzen Datensatz verallgemeinert werden.

So, das soll genug sein fuer heute und mit dem „Integralansatz“. … … … Da hat es die letzten zwei Beitraege dann doch noch geklappt mit den …

[…] Artikel mit Bildern und (meist) nicht ganz so viel Text […]

… naja, fast … viel Text ist’s immer noch, aber ich handle ja doch recht viel ab in nur zwei Artikeln; relativ gesehen ist‘ also wenig Text … tihihi.

Ich bin ueber den „Integralansatz“ erst im Laufe der Maxiserie gestolpert und habe mir das erst jetzt zum Ende alles nochmal damit angeschaut. Es ist beruhigend, dass ich damit hauptsaechlich meine vorherigen Ergebnisse bestaetige (und ein paar neue Erkentnisse erhalte). Aber wie mehrfach erwaehnt, wollte ich nicht alles nochmal im Detail machen. Ich habe naemlich wirklich keine Lust mehr und freue mich darauf, diese Maxiserie nach fast drei Jahren abzuschlieszen.
Aber keine Sorge, Letzteres passiert noch nicht heute, denn ich møchte nochmal auf alles zurueck schauen und das wird dann mindestens noch ein (vllt. zwei) Artikel.