Søren in Norwegen

Da ich viele Phaenomene schon ausfuehrlich diskutiert habe, kann ich heute ein paar Sachen zu den Selbstzitierungen kurz abhandeln.

Auch wenn es vorher schon los ging, so ist hier erst dieser vorherige Beitrag relevant, in dem ich linklevelabhaengige doppellogarithmischen Histogramme systematisch zeigte. Das muss ich nicht nochmal im Detail wiederholen und zeige in diesem Diagramm …

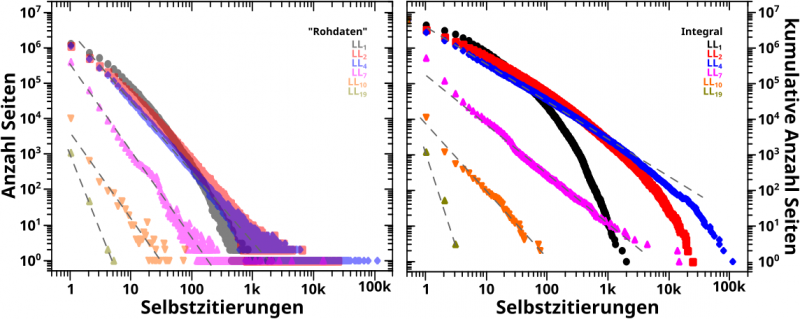
… nur ein paar repraesentative (integrierte) Histogramme. Links (mit den blassen Farben) zur Wiederholung die „Rohdaten“ und rechts die integrierten Daten.

Eigentlich gibt’s hier nichts weiter zu sagen, denn wieder bestaetigen die integrierten Daten die vormaligen Resultate mit høherer Genauigkeit.
Ich hatte damals besprochen, dass bei den ersten Linkleveln der lineare Zusammenhang nicht all zu gut ist; hier sieht man, dass es gut genug ist mindestens ab LL₄.
Ich habe die Anstiege nicht nochmal „vermessen“ (was ja vormals zu diesem ganz wunderbaren Resultat fuehrte), aber das sieht schon richtig aus und am wichtigsten ist ohnehin, dass die Anstiege mit zunehmendem Linklevel auch hier steiler werden.
Als Letztes ist noch zu sagen, dass man auch mittels Integralen nix machen kann, wenn da nix ist. Siehe die Daten zu LL₁₉.

Danach hatte ich den Startpunkt fuer die Simulation mit den realen Daten verglichen. Das war damals sehr gut und ist auch bei den Integralen sehr gut. Ich habe da zwar ein Diagramm, aber der Informationsinhalt ist so trivial, dass ich das nicht nochmal zeigen muss.

Aehnlich schnell und ohne Diagramm kann ich abhandeln, wie die integrierten Daten der durchschnittlichen Anzahl der Selbstzitierungen auf LL_i+1 in Abhaengigkeit von LL_i aussehen. Wieder bestaetigen die integrierten Daten vorherige Resultate. Es liegt aber die gleiche Situation wie bei den durchschnittlichen Links pro Zitat vor. Deswegen muss ich das nicht nochmal im Detail besprechen und das zugehørige Diagramm ist auch nicht so spannend.

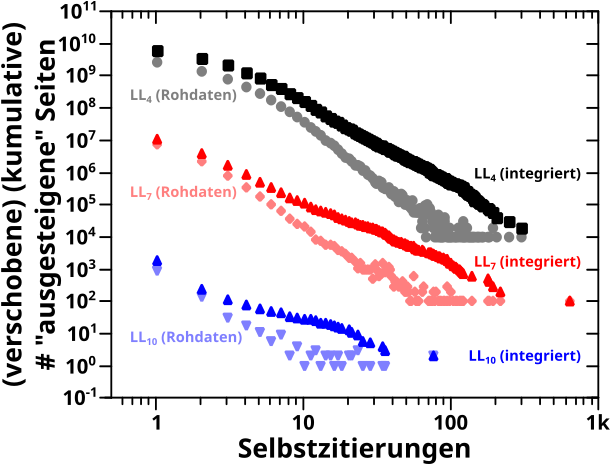
Als Letztes zu den Selbstreferenzen noch drei repraesentative Beispiele bzgl. der Seiten die von einem Linklevel zum naechsten „aussteigen“ aus der „Selbstreferenzkette“:

Die Daten sind gegeneinander verschoben und die „Rohdaten“ sind die Punkte mit den blassen Farben. Da man nur Phaenomene die bereits mehrfach besprochen wurden sieht, habe ich mir nicht mal mehr die Muehe gemacht „Regressionsgeraden“ von Hand rein zu legen … ich wollte das schlieszlich nicht alles nochmal machen, sondern nur gucken, was eine Integration zur Folge hat und das hier sieht alles gut und wie erwartet aus.

Das ging ja ausnahmsweise _wirklich_ mal schnell heute … fetzt ja.
Beim naechsten Mal schliesze ich die log-log-Plots ab und zeige ein paar Beispiele, bei denen eine Integration der falsche, oder zumindest ein nicht nuetzlicher Ansatz ist.