Søren in Norwegen

OIOIOI! Was fuer ein tolles Weihnachtsgeschenk, denn das hier heute ist sooo geil! Der Integralansatz hat naemlich bei der Verteilung der Grøsze der Archipele zu mehreren neuen Erkentnissen gefuehrt. Aber der Reihe nach.

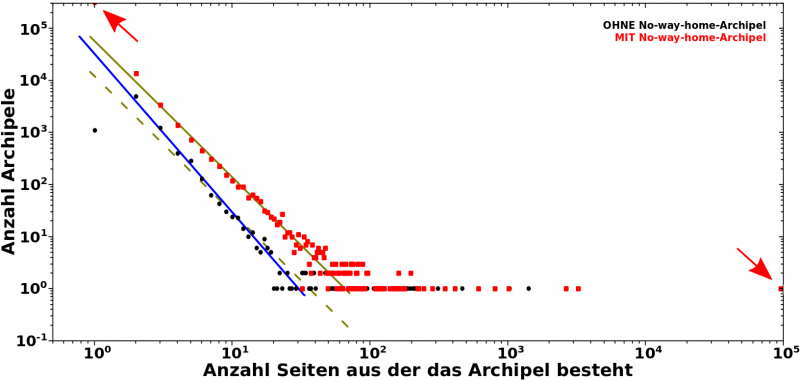
Zur Erinnerung nochmal das Diagramm von damals:

Das sind erstmal wieder „nur“ zwei „Histogramme mit Schwanz“. Damals unterschied ich zwischen der Verteilung bei der das No-way-home-Archipel (in kurz: nwhA) auszen vor gelassen wurde (schwarze Punkte) und der wo das mit drin war. Achtung: auch wenn ich hier die Einzahl benutze, so besteht das nwhA eigtl. aus mehreren No-way-home-ArchipelEN; inklusive mehreren zehntausend einzelnen Seiten.
Ich berechnte nie die Anstiege (der von Hand hereingelegten Linien), aber fuer die schwarzen Punkte (blaue Linie) ist selbiger ungefaehr -3.3 und fuer die roten Punkte (Linie in oliv) ca. -2.5. Das ist ein deutlicher Unterschied, aber aufgrund der Datenlage wollte ich nicht aussschlieszen, dass die linearen Bereiche der beiden Histogramme den gleichen (wenn nicht gar den selben) Anstieg haben — siehe die (parallel verschobene) gestrichelte Linie in oliv, welche die schwarzen Punkte nicht unbedingt viel schlechter beschreibt.

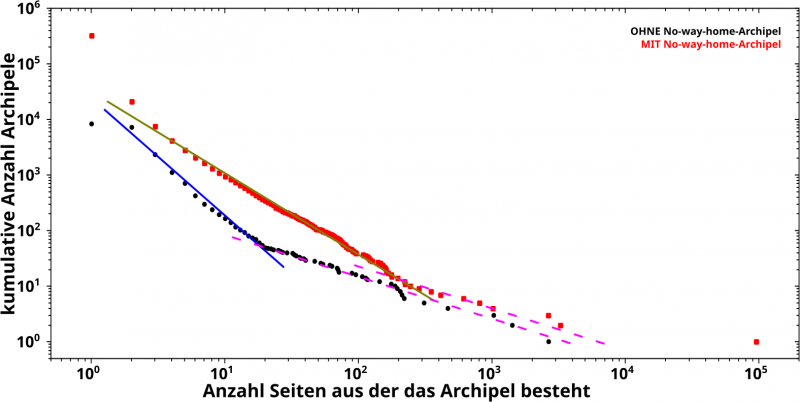
Die integrierten Daten (normale Integralgrenzen) sehen nun so aus:

OIOIOIOIOI! Das fetzt ja! Denn auf einmal treten mehrere Sachen deutlich hervor.

Zum Ersten sieht man, dass die Histogramme aus ZWEI Abschnitten mit unterschiedlichen Anstiegen bestehen. Diese Information war im obigen Diagramm komplett im „Zappelschwanz“ versteckt. Toll wa!
Ich bezeichne den (jeweiligen) linken Abschnitt als „normale“ Archipele und den (jeweiligen) rechten Abschnitt als „grosze“ Archipele.

Zum Zweiten sind besagte Abschnitte ganz klar mittels vier Geraden (in doppellogarithmischer Darstellung) zu beschreiben. Aber Achtung: die zwei Geraden der jeweils ersten Abschnitte (die blaue und olive Linie) haben unterschiedliche Anstiege waehrend die der jeweils zweiten Abschnitte hingegen den gleichen Anstieg haben (die lila, gestrichelten Linien) … nun ja, innerhalb des Fehlers interpretiere ich das als den gleichen Anstieg; mathematisch betraegt der Unterschied aber nur ca. 0.1 und das habe ich bei allen vorhergehenden Untersuchungen immer als „das ist schon irgendwie das Gleiche“ durchgehen lassen.
Wieauchimmer, da faellt (fast) nix aus der Reihe mit einer Kruemmung oder groszen „Ausreiszern“

Aus diesen Beiden folgt das Dritte: die Seiten die die Daten der ersten Abschnitte ausmachen unterliegen jeweils anderen Potenzgesetzen, waehrend fuer die groszen Archipele der zweiten Abschnitte nur EIN Potenzgesetz gilt. Das ist nicht ungewøhnlich, dass fuer Daten-am-Ende-und-irgendwie-weit-auszerhalb-der-normalen-Verteilung andere Gesetze gelten und das tritt (relativ) haeufig auf; kurioserweise gelten (in anderen Zusammenhaengen) fuer solche Daten oft maechtige Gesetze waehrend das oft nicht den Rest (und Groszteil) der Messungen beschreiben.
Wieauchimmer, vom Bezuhgsrahmen ist abhaengig wann „grosze Archipele“ beginnen.

Viertens folgt aus dem kleineren Anstieg der zweiten Abschnitte, dass es deutlich mehr grosze Archipele gibt als es geben sollte im Vergleich mit den normalen Archipelen; das untermauert die Vermutung eines anderen Mechanismus fuer grosze Archipele.
Ich denke NICHT, dass diese Aussage (eines anderen zugrundeliegenden Mechanismus) fuer die ersten Abschnitte gilt, obwohl diese auch unterschiedliche Anstiege haben. Weiter unten erklaere ich warum.

Diese vier Sachen sind so fetzig, weil das ueberhaupt nicht ersichtlich ist im urspruenglichen Diagramm.

Fuenftens stimmen die Anstiege der Geraden der ersten Abschnitte mit -2.5 fuer die schwarzen Punkte (blaue Linie) bzw. -1,6 fuer die roten Punkte (Linie in oliv) „mathematisch (fast) perfekt“ mit den frueheren Ergebnissen ueberein. Dadurch werden diese (wieder mal) untermauert, aber (wieder mal) mit grøszerer „Sicherheit“.

Das wiederum fuehrt zu Sechstens: der obige erwaehnte Unterschied im Anstieg der beiden Verteilungen ist echt. Hier kann man das nicht mehr mit „innerhalb des Fehlers kønnte das auch gleich sein“ wegdiskutieren. Wenn man das No-way-home-Archipel auszen vor laeszt scheint ein anderer Mechanismus am wirken zu sein … zumindest war das meine erste Vermutung. Die bereitete mir aber aber „Bauchschmerzen“ denn auch wenn ich das fuer „grosze Archipele“ akzeptieren konnte (s.o.) so sind die schwarzen Punkte ja bei den roten Daten mit drin und ich konnte mir nicht erklaeren warum Seiten (in Archipelen) auszerhalb des nwhA sich anders verhalten sollten als wenn ich alles zusammen betrachte.

Diese Unstimmigkeit liesz mich (wieder einmal) nicht los und ich gruebelte (wieder einmal) tagelang darueber nach, wie das erklaert werden kønnte. Ich muss ganz ehrlich sagen, dass ich stolz auf mich bin, dass ich eine møgliche Erklaerung fand.
In kurz: das Phaenomen der Archipele kann _nur_ in seiner Ganzheit betrachten werden und sollte NICHT in das nwhA und Archipele auszerhalb desselbigen unterteilt werden.

Aber der Reihe nach und zunaecht muss man sich erinnern, dass ich („historisch“ gesehen) zuallererst das nwhA gefunden habe. Das reichte aber nicht aus um die damals untersuchte Diskrepanz zu erklaeren und ich stellte weitere Ueberlegungen an, bei denen ich das nwhA zunaechst auszen vor liesz und erst am Ende wieder alles verknuepfte. Die schwarzen Daten oben sind nun die Daten bei denen das nwhA NICHT mit dabei ist und die roten Punkte bei denen alles verknuepft ist.
Ich erwaehnte damals, dass das nwhA viele Verbindungen mit Archipelen hat welche in besagten (hier) „schwarzen Daten“ dargestellt sind; aber das sieht man NUR, wenn man wieder alles verknuepft.
Das muss man im Hinterkopf behalten bei den folgenden Erklaerungen, aber bevor ich zu denen komme, muss ich noch auf etwas anderes hinweisen.

Fuer die folgenden Ueberlegungen gilt, dass mich NUR der Anstieg und NICHT die „Amplitude“ der Kurven interessiert. Oder anders: die schwarzen Daten gehen schneller nach unten, aufgrund besagten (staerkeren) Anstiegs und das interessiert mich. Gleichzeitig sind sie auch nach unten „verschoben“ einfach weil die Anzahl der Archipele die in den roten Daten enthalten sind viel grøszer ist als die Anzahl der Archipele welche die schwarze Daten ausmachen. Diese absolute Verschiebung interessiert mich NICHT und fuer das was ich hierunter schreibe, nehme ich an, dass die „Amplituden“ gleich grosz sind.
Auszerdem rede ich im folgenden immer nur ueber die ersten Abschnitte in den obigen (integrierten) Daten.

Die schwarzen Daten unterliegen einem Potzengesetz welches schneller abfaellt als das Potenzgesetz welches die roten Daten beschreibt. Wenn besagte Gesetze nun in der Wahrscheinlichkeitsinterpretation betrachtet werden (mit dem was ich eben schrieb bedeutet dies Aussage, dass man sich denken soll, dass beide Verteilungen insgesamt gleich viele Archipele enthalten), dann heiszt das, dass die Wahrscheinlichkeit fuer ein „schwarzes Archipel“ der Grøsze 4 so grosz ist wie ein „rotes Archipel“ der Grøsze 6. Oder ein „schwarzes Archipel“ der Grøsze 10 ist so wahrscheinlich wie ein „rotes Archipel“ der Grøsze 18. Man sieht das, wenn man einfach zwei gleiche Funktionswert fuer die schwarzen bzw. roten Daten anschaut und vergleicht welche Archipelgrøszen dazu gehøren.
Oder anders: die blaue Linie ist von der roten Linie gesehen nach links „verschoben“ … aber nicht parallel verschoben (denn dann waeren die Anstiege ja gleich), sondern abhaengig vom Wert der Archipelgrøsze unterschiedlich, mit zunehmenden Unterschied je grøszer das Archipel … das ist also eher eine Rotation nach links, wobei die Kurve beim Archipelgrøszenwert zwei festgehalten wird (das ist also der „Drehpunkt“).

Ich schreibe das hier auf, als ob das das natuerlichste von der Welt waere. Ich brauchte aber eine ganze Weile bevor ich da drauf gekommen bin und verfolgte ein paar „Sackgassen“ bevor ich diesen Durchbruch hatte.
Und wenn man mal drueber nachdenkt, dann ist das schon erstmal komisch; warum sollte die Verschiebung vom Wert auf der Abszisse abhaengen. Ich komme darauf zurueck, aber um zu verstehen warum das sinnvoll ist, muessen wir wieder zu den Archipelen und den Seiten aus denen diese bestehen zurueck kommen.

Zunaechst das nwhA und davon sind fuer das zugrundeliegende Prinzip das ich beschreiben will nur die …

[…] „Einwohner“ der (isolierten) „Insel der […] Unzitierten“ […]

… von Interesse; also nur die Seiten, welche nach „drauszen“ zitieren aber nicht zitiert werden. Dieser Satz nach dem Semikolon ist wichtiger als er aussieht, denn diese Seiten zitieren auch zu den nicht-nwhA-Archipelen. Den Prozess „sehe“ ich aber nicht in den „schwarzen Daten“, denn selbige habe ich dadurch erhalte, indem ich die Seiten aus denen das nwhA besteht auszen vor gelassen habe. Oder anders: „Einwohner“ der „Insel der Unzitierten“ sind sowas aehnliches wie die „Anhaenger“ im Zusammenhang mit „Kettenseiten“, nur dass der „Zitierpfeil“ andersrum ist.
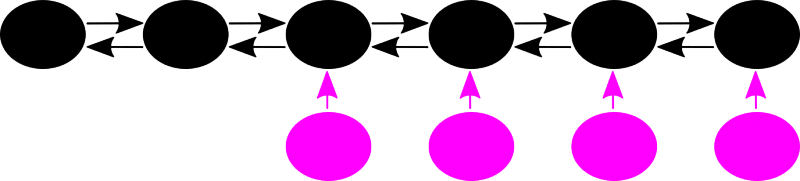
Ein Bild sagt oft (aber nicht immer) meht als 1000 Worte:

Schwarze Kugeln mit Doppelpfeilen gehøren zu einem NICHT-nwhA-Archipel, die lila Kugeln mit einem Pfeil hin zu Ersterem sind „Einwohner“ der „Insel der Unzitierten“.
Was wir hier sehen ist das was ich oben schrieb und was in den roten Daten ausgedrueckt ist: man darf nur alles zusammen betrachten. Die „schwarzen Daten“ sind Teil eines grøszeren Verbunds (die „roten Daten“), aber dieser Verbund ist „abgeschnitten“ wenn die Grøsze der Archipele bei den „schwarzen Daten“ bestimmt wurde.
Oder anders: wenn ein NICHT-nwhA-Archipel die Grøsze 6 hat, so ist dem nur scheinbar (!) so, denn eigentlich „kleben“ an vier Seiten dieses Archipels noch jeweils ein „Einwohner“ der „Insel der Unzitierten“ dran und die eigentliche Grøsze des gesamten Archipels ist 10.
Die ersten beiden schwarzen Punkte haben kein „Anhaengsel“, denn die sind ja der „Drehpunkt“.

TADA! Das ist die Erklaerung dafuer, warum die „schwarzen Daten“ KEINEM anderen Mechanismus unterliegen als die „roten Daten“ (denn das waere nicht sinnvoll), warum die aber dennoch durch ein anderes Potenzgesetz beschrieben werden.
Der Unterschied zwischen einem Anstieg von -2.6 und -3.3 wird genuegend gut durch (etwas-mehr-als)-eine-gruene-Kugel-pro-schwarzer-Kugel beschrieben. Das habe ich durchgerechnet. In Wahrheit ist das natuerlich oft komplizierter, wenn mal zwei (oder auch mal keine) Exraseite an eine schwarze Kugel „angeklebt“ wird.  ABER die „Insel der Unzitierten“ besteht aus ca. 320k „Einwohnern“ und dominiert das nwhA zu 90 Prozent. Solche komplizierteren Gegebenheiten kønnen in diesem einfachen Bild also ohne Beschraenkung der Allgemeinheit (oder so … ich habe das jetzt bestimmt nicht richtig gebraucht) auszen vor gelassen werden.

Gibt’s einen „Beweis“ dafuer?
Nun ja, keinen Beweis, denn dafuer muesste ich nachverfolgen, welche Seite wo „dranklebt“. Aber meiner Meinung nach starke Indizien, welche obiges Modell unterstuetzen.
Zum Einen verweise ich wieder auf die „Anhaenger“ bei den Kettenseiten. Einzelne Seiten die einfach an ’nem ausgedehnteren Konstrukt „dranhaengen“ sind ein bereits etabliertes Phaenomen.
Zum Zweiten sieht man es zwar nicht im Diagramm (wg. der logarithmischen Komprimierung), aber es „fehlen“ bei den „roten Daten“ bei der Archipelgrøsze 1 ca. 22-tausend Archipele. Das sind keine 320k (plus 1k aus den „schwarzen Daten“) sondern nur 299-tausend Archipele an der Stelle.
Zugleich sind es nur ca. 15-tausend Seiten die sich auf allen NICHT-nwhA-Archipelen „tummeln“ … das kønnte einem so vorkommen, als ob sich …

[…] (etwas-mehr-als)-eine-gruene-Kugel-pro-schwarzer-Kugel […]

… an diese ca. 15-tausend Seiten „ranklebt“. Fetzt wa!

Fuer diese zugrundeliegende „atomistische“ Erklaerung kann man in der Natur Beispiele finden (ich nenne mal nur Kohlenwasserstoffe) und deswegen klingt das Modell fuer mich durchaus plausibel. und ich hoffe, das war alles halbwegs verstaendlich erklaert.
Wie gesagt, bin ich voll stolz auf mich (und freu mich auch sehr dolle), dass ich das rausgefunden habe.

Ach so, das erklaert auch, warum der „Knick“ zu „groszen Archipelen“ bei den schwarzen Daten viel eher kommt als bei den roten Daten; die Archipele sind im eigentlich Verbund schon viel grøszer und damit in einem Bereich der wirklich einem anderen Mechanismus unterliegt.

Nochmal ach so: die „schwarzen Daten“ gibt es nur deshalb, wie ich das ganze urspruengliche Thema nach und nach „explorativ“ bearbeitet habe und nach und nach verschiedene Dinge entdeckte. In der Wissenschaft erzaehlt man dann am Ende alles halb „rueckwaerts“ und laeszt diese vorantastenden Schritte des langsamen Verstehens weg. Dadurch wird alles kuerzer und logischer und ergibt ein konsistentes Bild. Das ist aber nicht der Prozess des Forschens, den ich in dieser Maxiserie ja (mit Absicht) explizit darstelle.

Wieauchimmer, der Integralansatz ist hier sehr fruchtbar und das Alles sollte weiter untersucht werden … aber nicht von mir.

Das soll genug sein fuer heute. Mal schauen, was es naechstes Mal wird und ich wuensche erholsame Feiertage :)