Søren in Norwegen

Hier zeigte ich das erste Mal einen doppellogarithmischen Plot. Dabei untersuchte ich, wieviele Zitierungen eine Seite erhalten hat und erstellte davon ein Histogramm. Zu meiner (damaligen) Ueberraschung folgte das einem maechtigen Gesetz. Im linken Diagramm in diesem Bild …

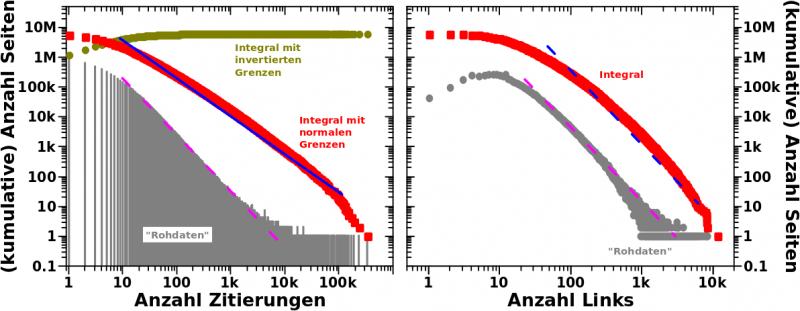
… ist in grau nochmals das vormalige Resultat wiedergegeben und die gestrichelte lila Linie deutet besagtes maechtiges Gesetz an. Wie beim vorletzten Mal erwaehnt, kann die Information im „Schwanz“ nicht benutzt werden. Deswegen integrierte ich die Daten (bzw. addierte diese, woraus die Benutzung des Wortes kumulativ folgt). Bei normalen Grenzen fuer das Integral (also von x bis x_max, bzw. Anzahl Zitierungen von Interesse bis zur maximalen Anzahl Zitierungen) sind das die roten Datenpunkte.
Hier passiert nun eine Sache, die im Folgenden vermutlich øfter auftreten wird: das sieht zwar immer noch halbwegs linear aus (die blaue Linie), aber wenn man genauer hinschaut ist das doch ein bisschen gekruemmt. Das folgt also nicht komplett einem maechtigen Gesetz, aber in diesem Fall ist die Abweichung vllt. klein genug, sodass diese mglw. (stueckweise) parametrisiert werden kønnten und die allgemeine Aussage erhalten bleibt.

Ich hab beide Linien nur mit dem Auge reingelegt weil ich keine Lust mehr auf genaue Analysen habe.
Fuer die Rohdaten erhalte ich einen Anstieg von ungefaehr -2. Nach der Mathematik muesste ich dann fuer die integrierten Daten einen Anstieg von -1 erhalten. Ich „messe“ ca. -5/4. Das passt also nicht ganz genau, aber ich wuerde das als gut genug gelten lassen. Gut ist, dass der (fast) lineare Zusammenhang fuer die roten Punkte auf der Abzsisse (fast) zwei Grøszenordnungen laenger gilt.
Mit obiger Aussage bzgl. der Parametrisierung behaupte ich, dass der Prozess der „Integralisierung“ hier erfolgreich (genug) ist, auch wenn nicht alles bis auf’s letzte i-Tuepfelchen genau passt.

Ganz kurz zu den Punkten in oliv: bei denen hatte ich die Integralgrenzen „invertiert“ (also von 1 bis x). Beim letzten Mal hatte ich das nur fuer das Beispiel mit dem positiven Exponenten gezeigt. Hier fuert die „Invertierung“ der Integralgrenzen zu aehnlichen „Phaenomenen“ wie ebenda besprochen wurden. Deswegen gehe ich da nicht nochmal im Detail drauf ein; ich wollte das aber mal gezeigt haben.

Damit kann ich zum rechten Diagramm uebergehen. Die Rohdaten sind das Histogramm bzgl. der Links pro Seite und das zeigte ich hier zum ersten Mal. Ich empfehle das damalige Bild nochmals anzuschauen, denn dort benutzte ich noch ein Balkendiagramm anstatt Punkte und mit Ersterem sieht die (von Hand hereingelegte) Linie (hier nochmal reproduziert in Form der gestrichelten, lila Linie) durchaus vernuenftig aus … weil zwischen 100 und 1000 kleinere Balken im „Balkenwald“ einfach nicht sichtbar sind. Deswegen habe ich das hier Punkte benutzt und dann sieht die Linie nicht mehr ganz so vernuenftig aus.
Und tatsaechlich, wenn man zum Integral uebergeht (wieder die roten Daten), dann sieht man da doch schon eine deutliche Kruemmung. Das ist also nicht wie im linken Diagramm, wo eine gewisse „Linearitaet“ durchaus angenommen werden kønnte.

Die blaue gestrichelte Linie ist die lila Linie nur parallel nach oben verschoben. Wenn ich das so mache, kønnte ich unter Umstaenden (wieder) fuer eine (stueckweise) parametrisierte Linearitat argumentieren … beim ersten draufschauen haut das durchaus hin. … Die Mathematik stimmt dann also nicht mehr.

Das ist also eher ein „vermutlich-nicht-linear-oder-ganz-vielleicht-mit-Augen-zudruecken-stueckweise-parametrisiert-linear-aber-wenn-dann-anders-als-ein-einfacher-log-log-Plot-vermuten-lassen-wuerde“-Fall.
Das fetzt natuerlich auch, denn auch wenn das meine damalige Aussage stark veraendert, vermutlich sogar negiert, so kommt man mittels „Integralisierung“ den wahren Gegebenheiten damit doch naeher.

Das soll genug sein fuer heute. Ist ja schøn, dass gleich die ersten zwei Faelle zwischen die zwei „Kategorien“ (Bestaetigung und Falsifizierung vorherger Ergebnisse) fallen. Das erste Diagramm ist naeher an der Bestaetigung, das zweite naeher an der Falsifizierung … aber ganz so einfach ist’s natuerlich nie … was das Ganze ja ueberhaupt erst interessant macht, nicht wahr :) .

Ich bin gespannt, was das naechste Mal bringt.