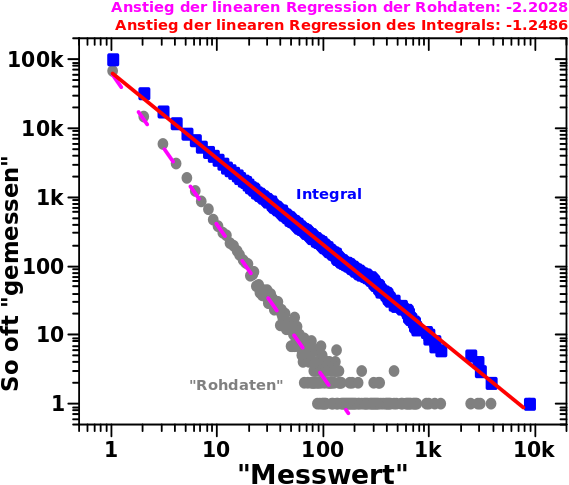
Ich versprach beim letzten Mal Freude und die kann man anhand dieses Diagramms erfahren:
Und wie so oft sage ich hier zunaechst mein beruehmtes: aber der Reihe nach … tihihi.
Die grauen, als „Rohdaten“ beschriftete, Punkte sind das Resultat einer Simulation. Bei dieser unterlag die Wahrscheinlichkeit einen gegebenen, ganzzahligen (!) „Messwert“ im Intervall [1, 10k] zu erhalten einem simplen Potenzgesetz mit einem Exponent von -2.23 und keinen Vorfaktoren oder anderweitigen Konstanten.
Ich machte 100-tausend „Messungen“ und zaehlte wie oft jeder Messwert auftrat. Hier ist also in den grauen Punkten (mal wieder) ein Histogramm zu sehen und das verhaelt sich wie erwartet; eine Gerade im log-log-Plot … zumindest bis zu Messwerten von ca. 100 (ganz konkret geschah der „Schnitt“ bei 130). Auch erwartet ist der „Schwanz“ bei Messwerten ueber 100 hinaus. Mit bspw. 1000-2.23 = 2 x 10-7 ist die Wahrscheinlichkeit zwar sehr klein aber eben nicht null und bei 100k Messungen ist das nicht unplausibel den Wert 1000 ein Mal zu messen. Das ist also ECHT! Das sind KEINE Ausreiszer!
Die hohen Messwerte muss ich aber „abschneiden“, um mittels linearer Regression (lila, nicht durchgehende Kurve) den Anstieg der Geraden zu -2.2028 ermitteln zu kønnen. Das ist gar nicht mal so schlecht, bedeutete aber in diesem konkreten Fall, dass ich 133 Messwerte ignorieren muste … schade eigentlich, nicht wahr.
Aber keine Sorge, Rettung naht in Form der blauen Punkte welche so berechnet wurden:
Weil es sich hierbei um diskrete Werte handelt kann das Integral als eine einfache Summe berechnet werden. Ich werde das aber weiterhin als Integral bezeichnen (und betrachten).
Die Grenzen des Integrals sind so zu verstehen, dass der Wert desselbigen bei einem gegebenen Messwert x die Summe ueber ALLE f(x) von dem gegebenen Messwert bis zum maximalen Messwert ist.
Das kann man auch anders ausdruecken, indem man f(x) derart normiert, dass die Flaeche unter der Kurve 1 wird (der Anstieg aendert sich dadurch ja nicht). Dann kann f(x) direkt als die Wahrscheinlichkeit angesehen werden x zu messen. Das ist leicht zu verstehen, insb. wenn man in Betracht zieht was (wie oben beschrieben) bei der Simulation passiert, wenn eine „Messung“ gemacht wurde.
Bei dieser „Wahrscheinlichkeitsinterpretation“ entspricht ein Integralwert zu einem gegebenen x der Wahrscheinlichkeit, dass eine Messung einen Wert produzieren wird der grøszer oder gleich x ist.
Diese Interpretation ist in vielen Situationen sehr hilfreich weswegen ich die hier erwaehne. Wirklich sinnvoll ist die aber nur fuer negative Exponenten (kleiner als -1).
Fuer positive Exponenten kommt man mit einer solchen Interpretation ganz schøn in die Bredouille; auch wenn die Mathematik natuerlich erhalten bleibt. Was der Grund ist, warum ich diese Interpretation eher vermeide und solche Normierungen im Weiteren nicht vornehme.
Zurueck zum Diagramm; man sieht leicht, dass ich bei den blauen Punkten auch Werte ueber 130 benutzen kann um den Anstieg selbiger zu ermitteln. Dieser betraegt -1.2486 und da es sich hierbei um das Integral handelt muss man dran denken, dass dieser um eins erniedrigt werden muss um den Exponenten zu erhalten.
Der Unterschied zum wahren (hier NICHT in Anfuehrungszeichen, da ich den exakten Exponenten fuer die Simulationen kenne) Wert betraegt fuer die „Rohdaten“ 0.0272 und fuer das Integral nur 0.0186. Letzteres ist also ca. 50% genauer. Der Unterschied hier ist aber nicht so wichtig (kann in anderen Zusammenhaengen aber wichtig werden.
Das Integral hat zwei (!) viel wichtigere Konsequenzen die weit ueber den kleineren Unterschied hinaus gehen. Zum Ersten muss ich KEINE (oder in anderen Zusammenhaengen weniger) Messwerte ausschlieszen UND zum Anderen ist der lineare Zusammenhang (hier auf der Abszisse) ueber zwei weitere Grøszenordnungen zu erkennen.
Ersteres ist selbsterklaerend und Letzteres ist krass urst gut, denn dadurch werden Ergebnisse robuster (und man kann denen dadurch noch mehr vertrauen).
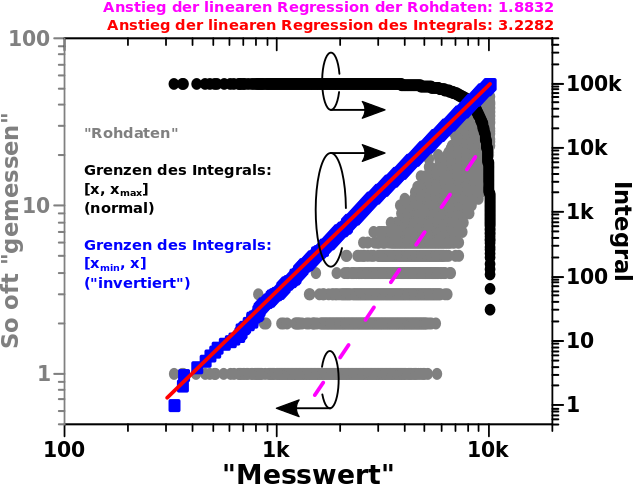
In einer zweiten Simulation aenderte ich das Vorzeichen (aber nicht den Wert) des Exponenten; grosze Messwerte sind damit viel wahrscheinlicher als kleine Messwerte und das spiegelt sich in den grauen Punkten (linke Abszisse) in diesem Diagramm wider:
Der grøszte Unterschied zum ersten Diagramm ist, dass es keinen „Schwanz“ (der in diesem Fall zu kleineren Werten gehen muesste) gibt. Demnach kann ich auch keine Messwerte „ignorieren“ bei der linearen Regression (lila, nicht durchgehende Kurve) und selbige fuehrt zu einem Anstieg von +1.8832 … was ganz schøn schlecht ist.
Wenn man nun das Integral mit den Grenzen wie oben bildet, erhaelt man die schwarze Kurve (rechte Abszisse). Da passiert erstmal gar nichts und dann ganz pløtzlich passiert was sehr schnell. Das wird verstaendlich, wenn man (ausnahmsweise) die „Wahrscheinlichkeitsinterpretation“ her nimmt. Bei derartigen Grenzen besagte diese, dass der Integralwert zu einem gegebenen Messwert angibt, wie grosz die Wahrscheinlichkeit ist, diesen oder einen høheren Messwert zu erhalten. Weil hohe Messwerte sehr viel wahrscheinlicher sind als kleine Messwerte aendert sich der Integralwert zunaechst nicht stark und dann pløtzlich urst dolle.
Die schwarzen Punkte bilden sicherlich keine Gerade und diese „komische Sache“ fuehrte bei mir zu gehørigem Kopfzerbrechen … worauf ich ja aber im nicht Detail eingehen wollte. Ich sage nur so viel: die Mathematik ist hier nicht „kaputt“. Das ist nur eine der Sachen bei der kontinuierliche Mathematik die von minus Unendlich bis plus Unendlich reicht mit echten diskreten Messwerten „kollidiert“, die nicht mal bis Null (wichtig!) und sicher nicht bis Unendlich reichen. Man kann das fixen und dann wird das wieder schøn gerade, auch bei diesen Grenzen … das war zwar interessant auszuknobeln, aber wie gesagt, das soll hier nicht das Thema sein.
Anstatt das kompliziert zu machen gebe ich die viel einfachere Løsung (welche man in den blauen Punkten (auch rechte Abszisse) sieht) direkt an — „invertierte“ Integralgrenzen:
In der „Wahrscheinlichkeitsinterpretation“ wuerde das der Aussage entsprechen, dass der Integralwert zu einem gegebenen x angibt, einen Messwert _kleiner_ oder gleich x zu erhalten … aber wie erwaehnt, kann man die „Rohdaten“ bei positiven Exponenten NICHT mehr streng als Wahrscheinlichkeiten interpretieren (auszer in ganz konkreten Beispielen mit endlichen Messungen). Ich fand das nur so anschaulich, weswegen ich das erwaehne … aber das „vergesst“ ihr, meine lieben Leserinnen und Leser, ganz schnell wieder und merkt euch nur die schnelle Løsung um auch bei positiven Exponenten Geraden in log-log-Plots von Integralen zu erhalten.
Zum Glueck tritt dieser Fall zumindest bei der Analyse des Wikipedianetzwerkes nicht so haeufig auf.
Wieauchimmer, die lineare Regression des Integrals fuehrt zu einem Anstieg der blauen Punkte von +3.2282, was auch um eins reduziert werden muss und dann sehr nah am wahren Wert ist … das ist mal echt urst cool, wa!
Genug fuer heute. Beim naechsten Mal fange ich an, nochmal durch (fast) alle doppellogarithmischen Diagramme durch zu gehen. Das werden also ein paar Artikel. ABER ich schaue mir das nicht nochmal im Detail an; das werden also Artikel mit Bildern und (meist) nicht ganz so viel Text wie hier … mit der Ausnahme, wenn es was Neues oder Interessantes zu sehen gibt.
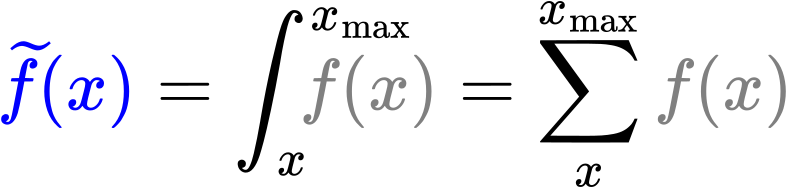
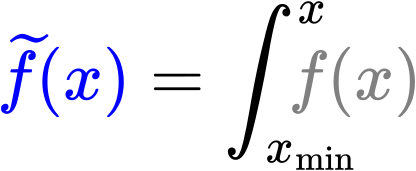
Leave a Reply