Heute geht’s mal schnell, denn ich mache nur die mathematische Einfuehrung zu dem was in den kommenden Artikeln kommt.
Hier begruendete ich, warum ich so gerne doppellogarithmische Plots zeige. Kurz zusammengefasst ist das so eine tolle Darstellungsweise, weil ich bei einem funktionalen Zusammenhang welcher einem Potenzgesetz …
… folgt, dann eine lineare Funktion …
… erhalte und der Anstieg der linearen Funktion in doppellogarithmisher Darstellung entspricht dem Exponenten in normaler Darstellung.
Das ist schon fetzig … aber beinhaltet oft auch einen subjektiven Faktor. Man muss naemlich schauen, welche im „Schwanz rumzappelnden“ Datenpunkte ignoriert werden muessen, damit die Gerade schøn passt; siehe bspw. hier, hier oder hier.
Nun beinhaltet der Schwanz aber mglw. noch Information. Ich brauchte viele Stunden mit Nachdenken, Probieren und Neuanalysiern bevor ich das Folgende wenigstens halbwegs verstanden hatte. Darauf gehe ich aber nicht naeher ein und sage kurz und knapp, dass man an besagte Information ran kommen kann, wenn man die Funktionswerte integriert.
Unter der Annahme, dass eine Grøsze sich nach einem maechtigen Gesetz verhaelt, ist das anhand eines Beispiels schnell erklaert. Mathematisch ist das sowieso ganz einfach, denn das Integral eines Potenzgesetzes …
… ist immer noch ein Potenzgesetz, nur mit einem um eins erhøhten Exponenten (und einem leicht veraenderten Vorfaktor, der interessiert hier aber nicht weiter und ich lasse den im Folgenden weg). Jaja, das ist ein unbestimmtes Integral und ich habe die Konstante weggelassen … das wird aber letztlich unten ein bestimmtes Integral, die Grenzen muessen aber diskutiert werden, und es geht doch sowieso nur um den Exponenten.
Obige Aequivalenz gilt natuerlich weiterhin …
… und das ist mal urst geil, denn unser Exponent A ist auch beim Integral der Funktionswerte unveraendert der Anstieg im log-log-Plot nur eben um eins erhøht … das absolute Glied ist anders, aber das interessiert uns meist eh nicht weiter.
Die Mathematik ist schøn (im aesthetischen Sinne) simpel und war nicht der Grund warum ich so lange brauchte das halbwegs zu verstehen. Vielmehr lag es daran, weil die Resultate aus der Anwendung besagter Mathematik auf meine bisherigen Ergebnisse nochmal interpretiert und verstanden werden mussten; Letzteres galt insb. fuer „komische“ Sachen … aber wie gesagt, darauf wollte ich nicht weiter eingehen … das passt hier nicht rein.
Warum mich das alles nun so sehr begeistert wird beim naechsten Mal ersichtlicher … *froi*.
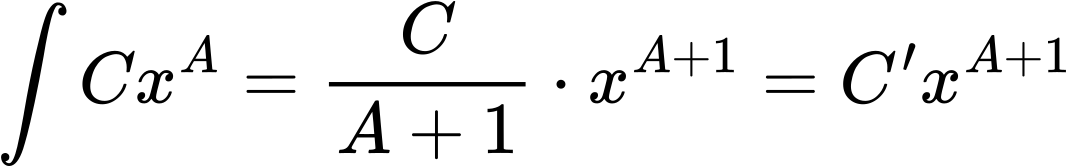
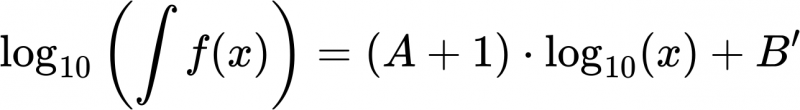
Leave a Reply