Søren in Norwegen

Beim letzten Mal erklaerte ich, dass man mittels der Anzahl den „Volumenanteil“ der Kettenseiten an allen Zitaten als Ordnungsparameter gewinnen kann. Ich zeigte wie sich die Anzahl der zitierten Seiten entwickelt und schloss mit drei Problemen ab:

Zum Ersten zitieren Kettenseiten auch andere Seiten. Zum Zweiten bewegt sich das Ensemble nicht als Diracsche δ-Funktion durch die Kette, sondern mit endlicher Breite (es kommt also zum Ueberlapp bei den Zitaten). Zum Dritten gibt es mehr als eine Kette.

Bzgl. der zitierten Seiten an sich ist das nicht so schlimm, muss aber diskutiert werden bzgl. des „Volumenanteils“ der Kettenseiten an allen Zitaten.
Ersteres ist handhabbar, denn der Anteil der Ketten an allen zitierten Seiten ist bei fruehen Linkleveln sehr klein, und bei spaeten deutlich grøszer. Fuer eine Abschaetzung nehme ich 5 Millionen Seiten am Anfang. Die Anzahl der Ketten ist unbekannt, aber aus den Ergebnissen die ich habe  _ueber_abschaetze ich die auf 5000 fuer kleine Linklevel. Wenn man das so macht, erhaelt man einen „Volumenanteil“ von 0.1 %.
Nota bene: hier darf man NICHT die Anzahl aller Kettenseiten nehmen sondern nur die Anzahl der Ketten, denn auf jedem Linklevel (auch auf kleinen) wird immer nur eine Seite (oder zwei) einer Kette zitiert … … … OKOK, streng genommen muesste man die Anzahl der Familien mit der Breite des jeweiligen Kettensignals multiplizieren; das waere aber nur ein konstanter Faktor fuer alle Linklevel und kann somit weggelassen werden)
Bei hohen Linkleveln gibt es NUR noch Ketten. Jede von diesen zitiert im Durchschnitt 10 bis 30 andere Seiten was ich zu 50 Zitaten _ueber_abschaetze. Das fuehrt zu einem Volumenanteil von 2 %. Das ist immer noch wenig, aber fast anderthalb Grøszenordnungen besser und ich denke durchaus „messbar“.
Bei einer realistischen Abschaetzung (weniger Familien am Anfang und weniger durchschnittliche Zitate per Seite) verbessert sich das Signal um etwas mehr als zwei Grøszenordnungen.

Das Zweite Problem kønnte man vermutlich durch extremes Erbsenzaehlen verhindern. Da habe ich aber sowas von gar keine Lust drauf und muss dann halt damit leben, dass das Signal insb. bei høheren Linkleveln stark schwankt. So lange das qualitativ alles stimmt, reicht mir das und ich tue einfach so, als wenn sich das Ensemble wie eine Diracsche δ-Funktion durch die Ketten bewegt.

Das dritte Problem ist massiv, denn ich kenne die Anzahl der Familien fuer kleine Linklevel nicht bzw. enthaelt diese Zahl waerend des Phasenuebergangs gewisse Unsicherheiten.
Die erste Sache kann ich aus den bereits oben verlinkten bisherigen Ergebnissen abschaetzen und ich setze die Anzahl Anzahl der Familien auf konstant 1000 fuer Linklevel kleiner LL₉. Bzgl. der zweiten Sache kønnte ich wieder durch Erbsenzaehlen die Unsicherheit minimieren … oder an die Sache herangehen wie ich es bezueglich des zweiten Problems mache: es reicht mir, wenn das qualitativ stimmt.

Ach so, ganz wichtig ist das was ich hier im „[w]ichtige[n] Einschub“ sagte. Denn auch wenn ich eine Kette nicht mehr erkenne, so bewegen sich die Nachzuegler noch drei weitere Linklevel darin und das muss man mitzaehlen. Das fuehrt dann bspw. dazu, dass bis LL₁₁ die Anzahl der Familien als 1000 angenommen wird.

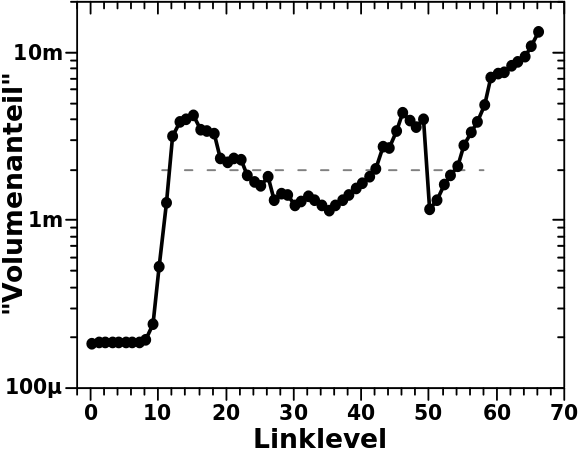
Nimmt man nun die Anzahl der Familien und dividiert diese durch die Anzahl der zitierten Seiten (beides pro Linklevel) erhaelt man den „Volumenanteil“ der Kettenseiten an allen Zitaten (wie so oft dienen die Linien zwischen den Punkten nur zur Besserung Fuehrung des Auges):

AHA! Das ist zwar alles ein bisschen krumm und schief, aber die Werte sind klein bei kleinen Linkleveln, nehmen ab LL₉ sehr schnell zu und erreichen schon bei LL₁₂ einen Plateauwert. Die Zunahme betraegt etwas mehr als eine Grøszenordnung zwischen dem „Grundniveau“ bei kleinem Linkleveln und dem ungefaehren Mittelwert des Plateaus (die graue, gestrichelte Linie ist NICHT der genaue, berechnete Mittelwert; die habe ich nur so Pi-mal-Daumen reingelegt). Besagte Zunahme ist also echt und so wie das qualitativ aussieht wuerde ich das von einem Ordnungsparameter erwarten.
Wie erwartet schwankt der Plateuwert. Die Schwankungen betragen nur ca. einen Faktor zwei um den Mittelwert. Qualitativ kann man sagen, dass der Wert konstant ist … wie ich es von einem Ordnungsparameter erwarten wuerde. Das ist ein GANZ wichtiger Unterschied zur Anzahl der zitierten Seiten, welche ja auch bei groszen und ganz groszen Linkleveln stetig abnimmt (also NICHT konstant ist).

Ich gehe nur bis LL₆₆ weil ich nur bis dort die Familien gezaehlt habe. Eigentlich geht das noch ein paar Linklevel weiter; siehe der Hinweis auf den „wichtigen Einschub“ oben. Das tut aber nix zur Sache.
Apropos ganz hohe Linklevel; ich wuerde NICHT sagen, dass der „Volumenanteil“ ab LL₅₀ einen weiteren Sprung macht. Hier ist nur noch das „São Paulo FC“-Artefakt ueber UND dessen Signal in der Linkfrequenz ueberlappt ueber mehrere Jahre. Ab LL₅₀ wird demnach nur noch eine Familie durch die Zitate aller (ueberlappenden) Jahre geteilt. Weil dann aber mehr und mehr Vorlaefer „raus fallen“ nimmt der Teiler irgendwann immer mehr ab und das sieht aus wie’n stetiger Anstieg.

Eine Sache bleibt noch und das ist der kleine Absolutwert des Plateaus. Bei „Volumenanteil“ wuerde ich erwarten, dass der gegen Eins geht, die gestrichelte Linie liegt aber bei 0.002, also 1/500 von 1.
Das machte mich etwas stutzig aber zumindest einen Teil des Raetsels konnte ich schnell løsen und ist wieder „nur“ Problem #2. Wenn sich das Ensemble durch die Ketten bewegt tut es das eben nicht wie eine Diracsche δ-Funktion. Vielmehr sind immer mehrere Kettenseiten „aktiviert“ weil die Antwortfunktion (in Form der Linkfrequenz) eine endliche Breite hat. Bei obigen Betrachtungen habe ich diesen Aspekt ja mit Absicht auszer Acht gelassen. Ich wuerde sagen, dass 10 Linklevel im Schnitt ueberdeckt werden … eigtl. 11 mit Reflexionen (von denen ich annehme, dass die meistens auftreten) und 9 ohne Reflexion und dann weniger wenn man sich dem Ende einer Kette naehert … alles nicht so einfach, aber 10 Linklevel Ueberdeckung fuehlt sich brauchbar an und damit kann man leicht rechnen. Diesen Sachverhalt mit einbezogen wuerde die gestrichelte Linine bei 0.02 liegen.

Nun wird fuer den „Volumenanteil“ die Anzahl der Familien durch die Anzahl der zitierten Seiten geteilt. Bei einem Wert von 0.02 wuerde das aber durchschnittlich 50 zitierten Seiten entsprechen. Das liegt zwar immer noch innerhalb meiner ersten (konservativen) Abschaetzung waere aber ca. einen Faktor zwei grøszer als was ich von normalen Wikipediaseiten annehmen wuerde. Und ehrlich gesagt, so kønnte das schon so sein, denn die Ketten sind ja oft Listen die etwas aus einem bestimmten Jahr aufzaehlen. Ich griff zufaellig 1885 in Australian literature heraus und zaehle 31 Links … mhmmm … das liegt zwar an der oberen Grenze fuer normale Seiten aber doch noch ca. den Faktor 2 entfernt von 50.
Deswegen schaute ich mal systematisch und die Kettenseiten auf LL₂₀ (22 an der Zahl) haben im Durchschnitt tatsaechlich 40 Links. Fuer LL₁₀ sind es sogar 44 Links und von den dort gefundenen 1860 Kettenseiten (ACHTUNG: das hier und hier Gesagte gilt aber fuer eine Abschaetzung muss ich das nicht betrachten … zumal die „falschen Ketten“ (und deren Links) ja sowieso in der obigen Rechnung mit benutzt werden) haben ueber 15 % mehr als 50 Links. So hat bspw. die List of members of the 3rd Jatiya Sangsad 605 Links. Wenn das oft genug passiert, wird der (durchschnittlichen) Wert des Divisors fuer den „Volumenanteil“ genug angehoben um naeher an die 50 zu kommen.
Wieauchimmer, 40 oder 44 durchschnittliche Links pro Kettenseite bring die gestrichelte Linie nahe genug an die Eins, sodass ich diese Diskrepanz als geløst betrachte.

Dies alles besprochen halte ich fest, dass man als einen (!) Ordnungsparamater den „Volumenanteil“ der Kettenseiten an allen Zitaten hernehmen kann UND dass dieser sich so verhaelt wie man das erwarten wuerde. Leider ist der „Volumenanteil“ umstaendlich zu berechnen und mit gewissen Nachteilen behaftet. Deswegen stellt sich die Frage: geht das nicht auch einfacher? … Und die Antwort ist JA! Sogar ueberraschend viel einfacher. Aber das muss genau diskutiert und mit einem bestaetigten Ordnungsparameter (dem „Volumenanteil“) verglichen werden, weswegen ich das auf das naechste Mal verschiebe.