Søren in Norwegen

Wenn, wie beim letzten Mal etabliert, das Ensemble aller Wikipediaseiten zwei Zustaende hat und es zu einem Phasenuebergang vom Einen in den Anderen kommt, so …

[…] stellt sich die Frage des Ordnungsparameters […].

Dafuer muss ich etwas weiter ausholen und man denke sich zunaechst einen (riesigen) Haufen mit gut durchmischten Legosteinen (der Einfachheit halber denke man sich den ikonischen 2×2 Stein, in verschiedenen Farben). Der Legosteinhaufen ist ein isotropes System. Das bedeutet, dass egal in welche Richtung ich einen Stab durch den Haufenstecke (von oben, unten, schraeg von hinten), so wird dieser (um Durchschnitt) immer gleich viele Steine und gleich viele Farben beruehren. Isotrope Systeme haben eine hohe Symmetrie und das ist voll toll, denn dadurch braucht man weniger Parameter um die zu beschreiben. Beim Stab ist die Orientierung vøllig egal, es kommt immer das Gleiche raus.
Trotz (oder wegen?) hoher Symmetrie ist andererseits die „Ordnung“ des Systems klein; der Haufen ist schlieszlich bunt durchmischt. Oder anders: der Ordnungsparameter ist null.

Nun stecke man die urst vielen Legosteine auf eine gigantische runde (!) Grundplatte (aber immer noch gut gemischt). Pløtzlich ist die Richtung des Stabes NICHT mehr egal. In der Ebene macht die Orientierung nichts aus, da gilt das Gleiche wie vorher. Aber wenn man den Stab senkrecht zur Ebene orientiert, dann sieht der immer nur noch einen Stein mit einer Farbe. Das System der Legosteine ist nicht mehr isotrop, die Symmetrie ist gebrochen und man braucht einen weiteren Parameter um Selbiges vollstaendig beschreiben zu kønnen. Anders ausgedrueckt: durch den Symmetriebruch hat die Ordnung des Systems zugenommen.
Wenn man dann auch noch die Farben sortiert, benøtigt man einen weiteren Ordnungsparamter um das System nach dem Farbensortierphasenuebergang vollstaendig beschreiben zu kønnen

Im System des Wikipedialinknetzwerkes „wuselt“ das Ensemble aller Seiten vor dem Phasenuebergang ungeordnet umher und „kollidiert“ (via Zitate) mit allen (!) anderen Seiten. Nach dem Phasenuebergang bewegt es sich geordnet in den Ketten, von einer Kettenseite zur naechsten und kollidiert im einfachsten Bild nur noch mit den Kettenseiten.
In diesem einfachsten Bild bietet sich also der „Volumenanteil“ der Kettenseiten an allen Zitaten als Ordnungsparameter an. Dieser Anteil ist (nahe) Null vor dem Phasenuebergang und (um einfachsten Bild) eins danach.

Um besagten „Volumenanteil“ zu bestimmen muss man zunaechst wissen, wieviele Seiten pro Linklevel zitiert werden. Dazu  kann ich wieder die Linkfrequenz zu Hilfe nehmen.
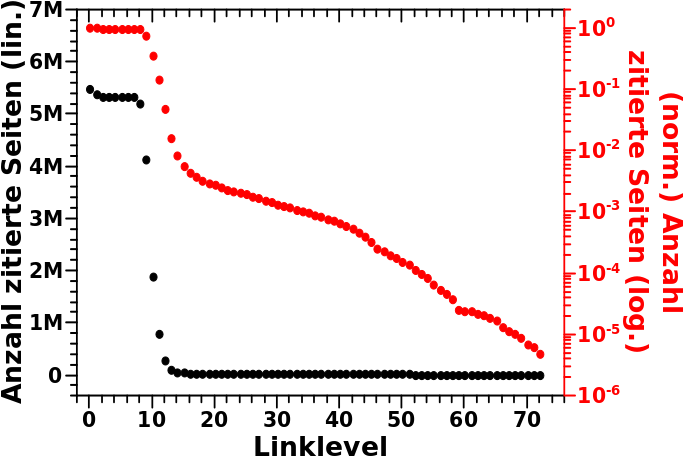
Zur Erinnerung: bei der Linkfrequenz schaue ich ob Seite X auf einem gegebenen Linklevel Seite A zitiert; ist das der Fall, geht der Zaehler fuer dieses Linklevel fuer Seite A um eins hoch. Zitiert nun Seite Q ebenso Seite auf auf dem selben Linklevel, geht der Zaehler um noch eins hoch. Wenn ich nun fuer jede Seite und jedes Linklevel NUR schaue ob der Zaehler ungleich null ist, finde ich raus, wie viele Seiten pro Linklevel zitiert werden. Es kommt also zu einer weiteren Informationskomprimierung und das Ergebniss ist die schwarze Kurve in diesem Diagramm:

Toll wa! Die schwarze Kurve sieht doch schon fast so aus wie’n Ordnungsparameter … das Wørtchen „fast“ ist wichtig, denn leider ist die Entwicklung der schwarzen Kurve „falsch herum“ dafuer; von viel zu wenig anstatt von wenig zu viel wie oben beschrieben.
Bei der roten Kurve wurden die Daten auf die Anzahl aller zitierten Seiten normiert und mit logarithmischer Skala dargestellt. Durch die „logarithmische Streckung“ sieht man, dass fuer diese Grøsze noch ziemlich viel „nach hinten raus“ passiert und das passiert natuerlich, weil das reale Daten sind, welche sich nicht nach dem einfachsten Ansatz verhalten. und bei realen Daten hat man drei Schwierigkeiten. Zum Ersten zitieren Kettenseiten auch andere Seiten. Zum Zweiten bewegt sich das Ensemble nicht als Diracsche δ-Funktion durch die Kette, sondern mit endlicher Breite (es kommt also zum Ueberlapp bei den Zitaten). Zum Dritten gibt es mehr als eine Kette.

Damit der Artikel nicht so lange wird, verschiebe ich den Rest auf das naechste Mal.