Søren in Norwegen

Nach den linklevelabhaengigen Verteilungen der Linkfrequenz folgt die Abhaengigkeit der Linkfrequenz auf einem Linklevel vom Wert der Linkfrequenz auf dem Linklevel davor.
Gleichartige Untersuchungen waren bei den Selbstreferenzen sehr fruchtbar und mindestens interessant bei den totalen (und neuen) Links. Bei denen hielt sich das „Gezappel“ der Datenpunkte in Grenzen und ich konnte relativ viele (repraesentative) Verteilungen zeigen.
Heute muss ich das kleinteilig aufdrøseln, …

… denn die Daten streuen zu sehr und wuerden sich gegenseitig ueberdecken, wenn ich bei kleinen Linkleveln mehr als eine Verteilung in das selbe Diagramm packen wuerde. Zum Glueck passiert nicht all zu viel Unerwartetes und alles kann ganz schnell generalisiert werden, sodass ich ingesamt nur wenige repraesentative Kurven zeigen muss. Aber der Reihe nach.

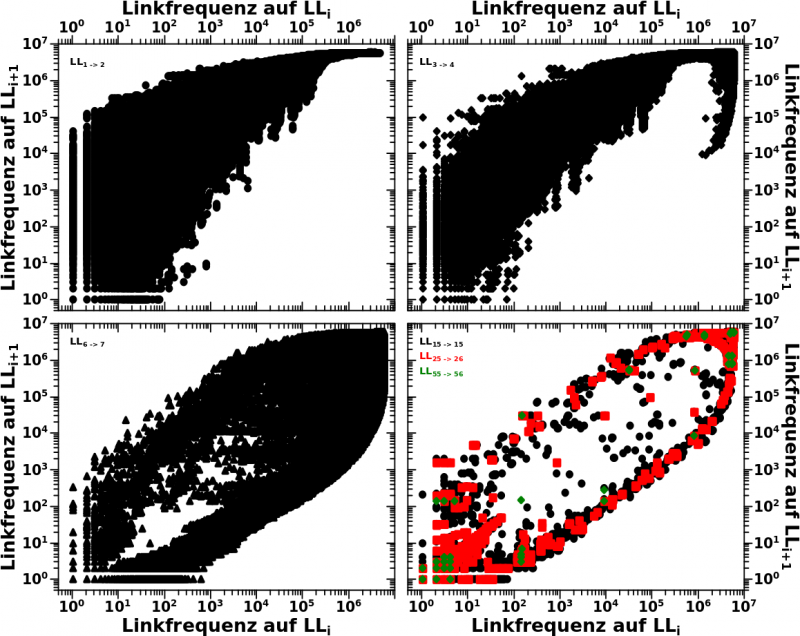
Der sich zu nach rechts oben zuspitzende Blob aus Punkten zeigt im Wesentlichen ein Resultat welches schon nach der allerersten Auswertung der zuallererst untersuchten Grøsze (der Summenverteilung der totalen Links) qualitativ hergeleitet werden kann. Es ist wieder eine Kombination aus drei bekannten Sachverhalten. Zum einen wenigen Links und daraus resultierenden wenigen Zitaten anderer Seiten auf LL₁. „Wenig“ bedeutet hier so ca. 1000 oder gar 10-tausend. Zum zweiten ein starker Anstieg der Anzahl von Links beim Uebergang zu LL₂ und dem daraus folgenden starken Anstieg der Linkfrequenz. So Pi mal Daumen und nur ganz schnell auf den Blob geschaut wuerd ich sagen, dass ein Anstieg um zwei Grøszenordnungen stattfindet … was gut (genug) mit den totalen Links uebereinstimmt. Zum dritten halten sich „beliebte Seiten“ nicht bei kleinen Zahlen auf und bilden die nach rechts oben zeigende „Spitze“.

Im rechten oberen Diagramm ist der Uebergang von LL₃ zu LL₄ zu sehen; es wurde also nur ein Schritt ausgelassen. Der „Blob“ bei kleinen Werten nimmt zwar ab, aber verschwindet nicht. Das ist auch sinnvoll, denn es gibt immer noch Seiten mit niedrigen Linkfrequenzen, mindestens die im „São Paulo FC“-Artefakt.
Die meisten Seiten hingegen befinden sich jetzt im (breiten)  Maximum bzgl. der Links die sie jetzt „sehen“. Da die Linkfrequenz aber nur zaehlt _ob_ und nicht wie oft eine Seite gezaehlt wird, gibt es eine „scharfe Kante“ bzgl. der Linkfrequenz. Und das macht sich im 90-Grad-Knick rechts oben bemerkbar. Im Maximum werden Seiten von anderen Seiten maximal zitiert und beim naechsten Schritt gilt das weiterhin (die Seiten befinden sich immer noch im Maximum, oder nicht weit weg davon). Das fuehrt dazu, dass sich viele Seiten in die obere Ecke draengen.
Weiterhin wissen wir bereits, dass das Maximum fast genauso schnell wie es angestiegen ist, auch wieder abfaellt. Die Datenpunkte befinden sich also auf der Abzsisse immer noch bei hohen Werten, brechen im naechsten Schritt aber um bis zu drei Grøszenordnungen auf der Ordinate ein. Das ist da wo die Kurve eine Wende macht und sich „auf dem Weg zurueck“ begibt.

Im linken unteren Diagramm ist die Entwicklung um weitere drei Linklevel voran geschritten. Die Daten beschreiben jetzt einen „Kreis“ (im uebertragenen Sinne). Die Kurve „zieht“ ihr Ende nicht mit (wie bspw. bei den „Orbits“ der totalen Links), sondern wird immer weiter gedehnt … wie ein Kaugummi. Die Erklaerungen sind im Wesentlichen wie oben.

Im rechten unteren Diagramm sind beispielhaft drei deutlich høhere Linklevel gezeigt. Das Bild aendert sich quantitativ, aber nicht qualitiativ; das „Gezappel“ nimmt ab (weil weniger Seiten ingesamt zitiert werden), aber der zugrundeliegende Mechanismus aendert sich nicht. Die gruenen Punkte replizieren dann (wieder einmal) die bereits bekannten Werte aus dem „São Paulo FC“-Artefakt (nur auf andere Weise).

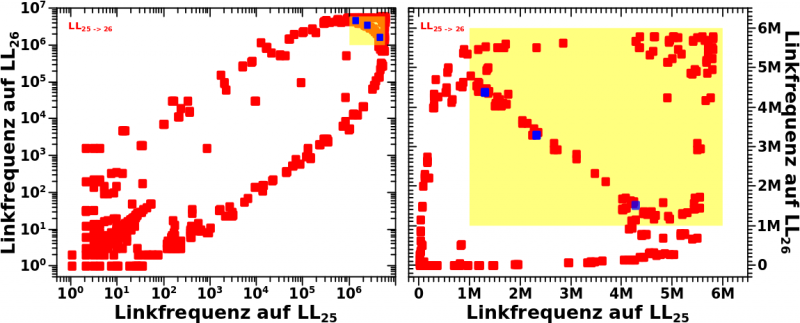
Mhmmm … also eigtl. scheint hier nix Interessantes zu passieren … bis man sich das Ganze mal (beispielhaft am Uebergang von LL₂₅ zu LL₂₆) in linearer Darstellung anschaut:

Wait! What!? Das aus der Ellipse ein Viereck wird verwundert mich nicht … aber wo zum Teufel kommt denn der Querbalken her? Ich muss das wohl wieder mal der Reihe nach angehen und nicht versuchen gleich alles auf einmal zu bearbeiten.

Zunaechst ist das gelbe Quadrat da mit Absicht drin. Es verdeutlicht ganz beeindruckend die logarithmische Komprimierung: bei linearer Darstellung sind die kleinen Werte, welche in der doppellogarithmischen Darstellung zu sehen sind, an den Rand und noch mehr in die Ecke gedraengt. Wir sehen die also „nicht“ mehr. Umgekehrt gilt natuerlich das Gleiche fuer grosze Werte.
Das ist natuerlich kein Nachteil der einen oder der anderen Darstellung. Beide sind sehr wertvoll und offenbaren unterschiedliche Informationen.

Was ist nun aber mit dem gigantischen Querbalken? Nun ja, der ist fuer die feine „innere Rundung“ in der logarithmischen Darstellung verantwortlich. Nach dem oben Besprochenen sollte es hier nur eine spitze Ecke geben (und die sehen wir ja auch). Durch den Querbalken, welcher (bei linearer Darstellung) Werte „in der Mitte des gelben Quadrats“ repraesentiert, wird die Bedingung der  „scharfe Kante“ aber „aufgeweicht“ und die Kurve nach innen abgerundet. Durch das Hervorheben von drei Datenpunkten versuche ich diesen Sachverhalt zu verdeutlichen.

Das soll fuer heute reichen. Ich habe den zugrundeliegend Mechanismus der zur Entstehung des „Kreises“ so ausfuehrlich behandelt, weil das Wissen darum nuetzlich wird, wenn ich beim naechsten Mal versuche der Entstehung des Querbalkens auf die Spur zu kommen.