Søren in Norwegen

Weil das „gemischten Verhalten“ der Linkfrequenzverteilungen so schwer zu interpretieren war, nahm ich mir beim letzten Mal vor mal zu schauen, wie sich das „Kollektiv“ der Wikipediaseiten von  niedrigen zu hohen Linkfrequenzen „bewegt“. Die schiere Datenmenge steht sich dabei selbst im Weg und deswegen entschied ich mich diese zu komprimieren und mir fuer jedes Linklevel nur anzuschauen …

[…] wieviele Seiten eigentlich in jeder Grøszenordnung „stecken“ […]

Ich gab auch eine kurze Erklaerung was ich damit meinte:

[…] ich [schaue] mir an, wie viele Seiten eine bis zehn Zitierungen, wie viele Seiten 11 bis 100 Zitierungen, wie viele Seiten 101 bis 1000 Zitierungen usw. usf. […] erhalten haben.

Das ist ein neues Konzept und recht viel auf einmal. Deswegen zeige ich erstmal wie das bei den totalen Links und den Selbstreferenzen aussieht, auch wenn man die „kolletkive Bewegung“ schon aus den einzeilnen Verteilunge ablesen kann.

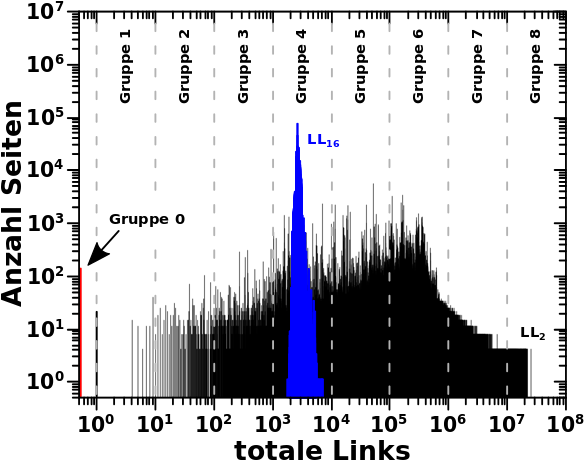
Zur Erinnerung sind hier alle Verteilungen bzgl. der totalen Links pro Linklevel zu sehen und ich zeige nochmal zwei (mehr oder weniger) repraesentative Verteilungen:

Die grauen gestrichelten Linien illustrieren einen Teil des Konzepts der Datenkomprimierung. Weiterhin ist auch gleich eine weitere Vereinfachung zu sehen; anstatt immer zu sagen „wie viele Seiten 11 bis 100 Zitierungen haben“ (usw. usf.) sag ich einfach (in diesem Fall) Gruppe 2. Die Gruppennummer ist dabei die Zehnerpotenz der oberen Grenze des Intervalls auf der Abszisse. Der Wert fuer die untere Grenze is i.A. der Wert de oberen Grenze geteilt durch 10. Der Wert an der oberen Grenze ist in der jeweiligen Gruppe enthalten, der an der unteren Grenze nicht. Die einzigen Ausnahmen sind Gruppe 0 und Gruppe 1 wegen der Besonerheiten der nullten Potenz. Zur Ersteren zaehlen NUR die Seiten, die den Nullwert annehmen (der rote Balken, der zu LL₂ gehørt). Zur Letzteren zaehle ich auch alle Seiten die den Wert eins annehmen.

Bei den zwei Beispielverteilungen wuerde ich also auf LL₂ erwarten, dass alle Gruppen einen Wert haben, waehrend auf LL₁₆ nur Gruppe 4 einen Wert hat.
Damit soll genug gesagt sein zum Prinzip und das ist das Ergebnis:

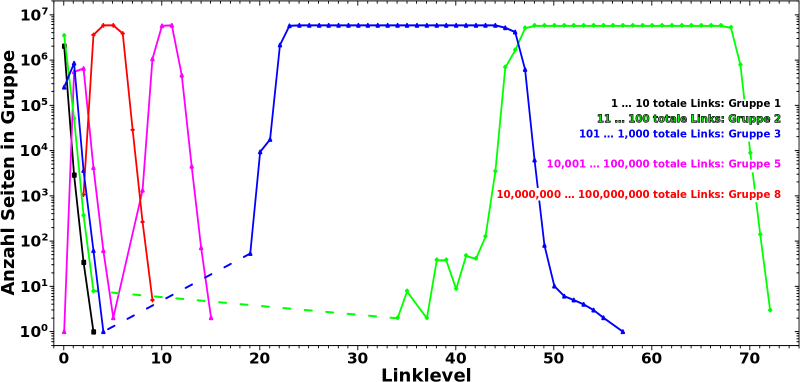
Weil das bei kleinen Linkleveln so unuebersichtlich ist habe ich nur ein paar repraesentative Gruppen reingepackt. Auszerdem ist das Diagramm ausnahmsweise laenger, damit man bei besagten kleinen Linkleveln nicht die Uebersicht verliert. Gestrichelte Linien verbinden Teile der Kurve einer Gruppe zwischen denen es keine Werte gibt.

Beim letzten Mal schrieb ich diesbzgl.:

Wikipediaseiten haben zuerst wenige, dann viel mehr, dann viel viel viel mehr totale Links um dann wieder weniger, viel weniger, viel viel viel weniger und letztlich gar keine Links mehr zu haben.

Und das ist genau das was man hier sieht … abgesehen von der letzten Aussage, weil ich Gruppe 0 weggelassen hab. Diese replizierte naemlich wieder nur ein altbekanntes Resultat, welches durch die ausfuehrliche und mehrfache Besprechung des „São Paulo FC“-Artefakts hinreichend bekannt ist. Aber der Reihe nach (und es mag helfen, wenn man das Gezappel der individuellen Verteilungen, die oben verlinkt sind, nochmal anschaut).

Auf LL₀ befinden sich (im Diagram) viele Seiten in den Gruppen 1 bis 3, nur eine Seite in Gruppe 5 und keine Seite in Gruppe 8. Auf LL₁ nimmt die Anzahl der Seiten in den drei erstgenannten Gruppen rapide ab, dafuer aber in Gruppe 5 rapide zu. Das ist die „kollektive Bewegung“ von der ich sprach. Auf LL₂ wird dann auch Gruppe 8 (zunaechst etwas zøgerlich) besetzt und von LL₃ bis LL₆ halten sich praktisch (fast) alle Seiten dort auf und die Gruppen 1 bis 3 sind komplett leergeraeumt.
Abe LL₇ setzt dann die „Rueckwaertsbewegung“ ein. Diese ist aber nicht so „chaotisch“ wie die „Vorwaertsbewegung“ und die Gruppen werden in absteigender Reihenfolge nach und nach gefuellt und dann wieder geleert, wenn die Seiten zur naechsttieferen Gruppe „weiterwandern“. Zunaechst natuerlich Gruppe 5, aber dann auch die Gruppen 3 und 2. Gruppe 1 wird nie wieder besetzt, da am Ende alle Seiten direkt von Gruppe 2 zu Gruppe 0 springen.

Das war letztlich easy peasy zu verstehen, insb. wenn man (wie bereits erwaehnt), das (oben verlinkte) Gezappel der linklevlabhaengigen Verteilungen der totalen Links sich nochmal anschaut.
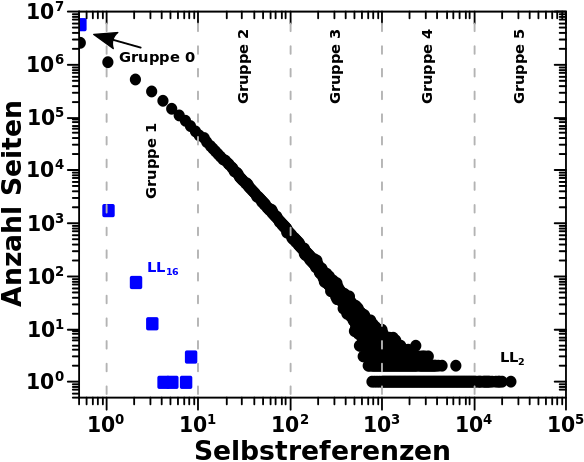
Deswegen geht’s gleich weiter mit den Selbstreferenzen. Zur Erinnerung zwei Beispielverteilungen:

Die Gruppen gehen nicht ganz so weit wie bei den totalen Links und nicht gezeigt ist Gruppe 6, weil sich da ueber alle Linklevel gesehen nur zwei Seiten aufhalten (siehe das naechste Diagramm). Von der Andersartigkeit der Verteilungen abgesehen (welche aber bereits ausfuehrlich besprochen wurde) gibt’s aber letztlich nichts Neues und deswegen geht’s gleich weiter mit den Seiten pro Grøszenordnung:

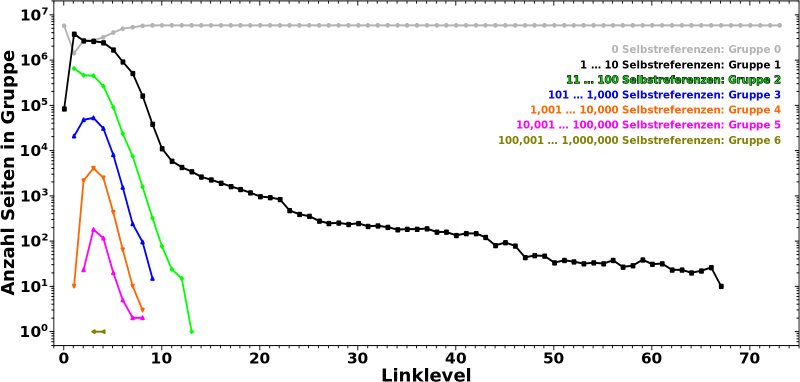
Das hier ist so viel uebersichtlicher, dass ich alle Gruppen dringelassen habe. Beim letzten Mal schrieb ich nur kurz:

[e]s ist viel wahrscheinlicher, dass eine Seite sehr wenige Selbstreferenzen als viele hat […]

… und das ist was man sieht; Gruppe 1 ist immer høher als Gruppe 2 ist immer høher als Gruppe 3 usw. usf. Das aendert sich auch dann nicht, wenn Gruppen die Seiten mit mehr (und viel mehr) Selbstreferenzen repraesentieren, bei LL₂ oder LL₃ ein høheres Signal aufweisen als am Anfang. Die Erhøhung kommt naemlich durch das Vorhandensein von mehr totalen Links zustande und wenn ich davon mehr habe, habe ich (dem maechtigen Gesetz entsrpechend) auch mehr Seiten in Gruppe 1.
Wieauchimmer, ab ungefaehr LL₁₀ befinden sich onehin die meisten Seiten in Gruppe 0 und es passiert nicht mehr wirklich was.

Alles in allem sind die Seiten pro Grøszenordnung sowohl fuer die totalen Links, als auch fuer die Selbstreferenzen leicht zu verstehen, da diese relativ direkt aus den Verteilungen pro Linklevel folgen. Das ist der Hauptgrund, warum ich zunaechst diese abgehandelt habe, damit man etwas vertrauter wird mit der Datenkomprimierung und was man da dann eigtl. sieht.
Das bedeutet aber auch, dass man fuer diese beiden Grøszen da nichts weiter „rausholen“ kann.
Beim naechsten Mal dann das Gleiche fuer die Linkfrequenzen. Das ist komplizierter und da passiert viel mehr.