Søren in Norwegen

Vor einer Weile entdeckte ich, dass die individuellen Verteilungen der Selbstreferenzen pro Linklevel maechtigen Gesetzen unterliegen. Das brachte mich auf die Idee mit der Simulation. Dafuer musste ich aber herausfinden, wie sich das System entwickelt. Dies wiederum vollbrachte ich mit einer Untersuchung der Abhaengigkeit der Anzahl der Selbstreferenzen auf einem Linklevel von der Anzahl der Selbstreferenzen auf dem Linklevel davor.
Ersteres hatte ich sowohl fuer die Anzahl aller, als auch die Anzahl neuer Links pro Linklevel getan und da kam eigtl. nix bei raus. Die Idee Letzters mal zu machen kam mir damals erst gar nicht. Das hole ich heute nach.

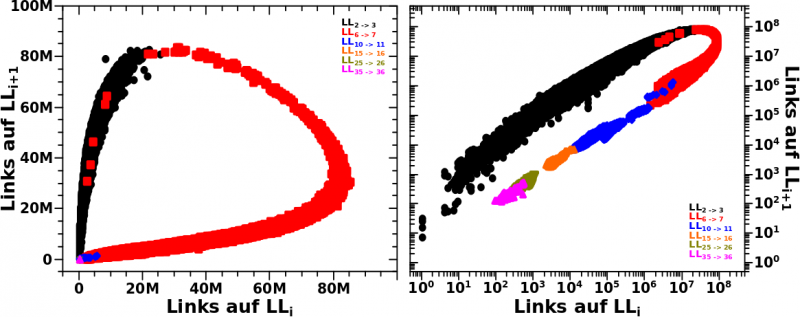
Zum Glueck muss ich nicht mehr erklaeren was ich hier eigentlich mache und kann sofort ohne viel Aufhebens repraesentative Kurven bzgl. der Anzahl der totalen Links zeigen:

WOW! … Das war meine erste Reaktion als ich das sah. Denn ich hatte obiges Nullergebniss, dass bei den (einfachen) individuellen Verteilungen nicht viel bei rum kam, noch im Hinterkopf. Aber dann praesentiert sich mir hier pløtzlich eine so wunderschøne Abhaengigkeit.

Das ist zwar nicht linear und die Entwicklung des Systems „macht ’ne Kurve und kehrt zurueck“, aber in der doppellogarithmischen Darstellung sieht das aus wie’n Ausschnitt aus ’ner Ellipse und Orbits sind mathematisch in geschlossener Form behandelbar. Das wuerde das Ganze nur etwas komplizierter machen, denn Orbits sind … ich sag jetzt mal im generellen Sinne … zeitabhaengig.
Oder anders: bei den Selbstreferenzen konnte ich einfach sagen, dass die Selbstreferenzen auf dem naechsten Linklevel NUR von den Selbstreferenzen auf dem jetzigen Linklevel abhaengen, aber nicht vom Linklevel selber. Das ist beim Orbit nicht mehr der Fall, denn solche sind keine bijektiven Abbildungen mehr sondern nur noch surjektive Abbildungen. Bei der Entwicklung muss man sich also „merken“ ob man auf dem oberen „Ast“ oder (schon) auf dem unteren „Ast“ ist, denn wenn ein Punkt sich noch auf Ersterem befindet, so soll dieser nicht einfach „runter springen“ sondern schøn „um die Kurve rumgehen“.

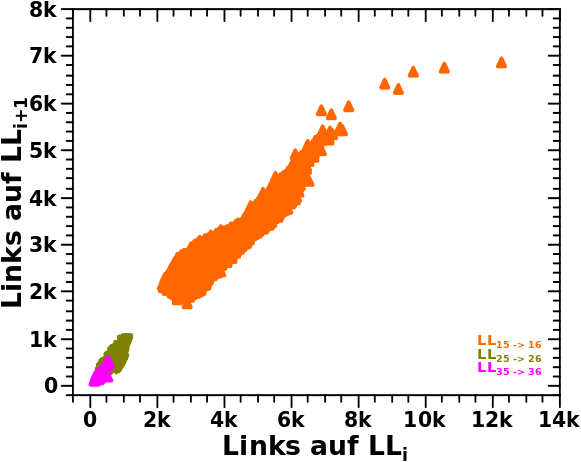
Aber Achtung, das ist keine wirkliche Ellipse, denn bei spaeteren Linkleveln verhaelt sich das auch bei linearen Achsen linear:

Aber selbst dann kønnte man das mathematisch noch als Bézier Kurve darstellen.

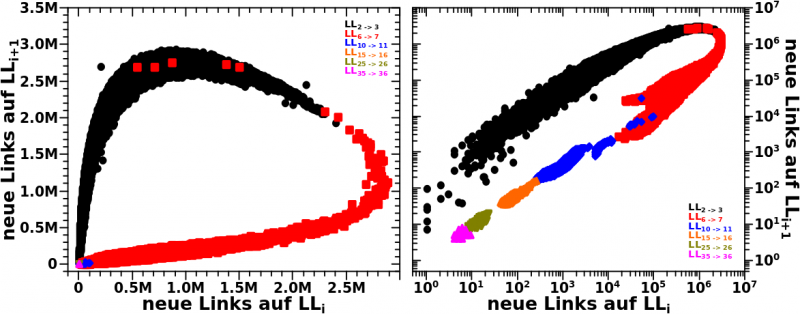
Bei den neuen Links ist das im Wesentlichen das Gleiche:

Die Skala reicht natuerlich nicht so weit und die neuen Links laufen den totalen Links „voraus“. Letzteres sieht man in der linearen Darstellung an den schwarzen Punkte fuer die neuen Links von LL₂ zu LL₃. Diese erreichen und ueberschreiten das Maximum bereits, waehrend das bei den totalen Links von LL₂ zu LL₃ noch nicht der Fall ist.
Aber das war zu erwarten und dieses Phaenomen des „Vorauseilens“ ist uns schon bei der Anzahl der neuen Links pro Linklevel im Vergleich zur Anzahl der totalen Links pro Linklevel ueber den Weg gelaufen, wo Erstere das Maximum eher erreichten als Letztere.

Lange Rede kurzer Sinn, auch die Entwicklung dieser beiden Grøszen kann man mathematisch beschreiben und dann prinzipiell mit nur einer Messung des Anfangszustands besagte Entwicklung des Systems berechnen. Das spare ich mir aber, denn ich habe da keine Lust mehr drauf.

Ach so, Aussteiger der totalen Links habe ich bereits gruendlich untersucht (und das Ergebniss kann auf neue Links uebertragen werden) und Ketten von neuen oder totalen Links kønnen per definitionem nicht reaktiviert werden.