Søren in Norwegen

Hier nochmal der Direktlink zur Tabelle mit den Daten.

Beim letzten Mal sagte ich, dass …

[…] mein jaehrliches Risiko […] ueberhaupt irgend einen Krebs zu bekommen […] nur 0.138 % [betraegt] […]

Wie kommt es dann aber, dass das Gesamtrisiko im Leben Krebs zu bekommen bei 50 % (und darueber) liegt? Dies ist nicht ganz einfach zu erklaeren unddeswegen der Reihe nach.

Alle Zahlen der Tabelle gehen davon aus, dass man nur ein Mal im Leben Krebs bekommt. Das ist nicht ganz richtig (und der Grund fuer komplizierte Korrekturen die ich hier erwaehnte) aber in Naeherung ist das gut genug.
Das unkorrigierte kumulative Risiko geht im Prinzip davon aus, dass es keinen „Verlust“ von Altersgruppe zu Altersgruppe gibt. Das bedeutet im Grunde, dass die Chance in der gegebenen Altersgruppe Krebs zu bekommen unabhaengig davon ist, in einer anderen (vorherigen) Altersgruppe Krebs zu bekommen. Oder anders: diese beiden Ereignisse sind inkompatibel (denn ansonsten haette ein Individuum es ja gar nicht bis zu der gegebenen Altersgruppe geschafft). Bei inkompatiblen Ereignissen greift das dritte Axiom von Kolmogorow und ich muss einfach nur die Summe aller (altersgruppenspezifischen) Einzelwahrscheinlichkeiten bis zur gegebenen Altersgruppe bilden, um das (unkorrigierte) kumulative Risiko zu erhalten.
Weil es so wichtig ist noch mal: bei dieser Rechnung gehe ich von meiner konkreten Situation aus. Ich nehme also an, dass es bis ins 43. Lebensjahr gekommen bin, OHNE dass Krebs diagnostiziert wurde.
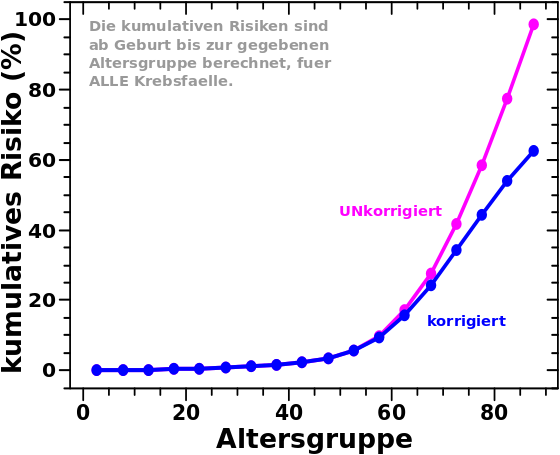
Fuer norwegische Maenner und alle Krebsdiagnosen zusammen drueckt sich das eben Geschriebene in der lila Kurve in diesem Diagramm aus:

Sehr gut: alle Wahrschienlichkeiten zusammen ergeben weniger als 100 % (so wie es sein muss … denn das Universum wuerde verpuffen, wenn die Summe aller Wahrscheinlichkeiten ueber 100 % liegt). Es ist auch gut, dass ich am Ende 100 % erreiche, denn wenn ich an nix anderem sterbe, dann bleibt ja nur noch Krebs als Todesursache uebrig.

Die Situation fuer einen frischgeschluepften Mensch muss aber anders angegangen werden. Es gilt auch fuer diesen neuen Menschen, dass man nur ein Mal Krebs bekommt. Nun muss man im Hinterkopf haben, dass die Statistiken NUR ueber Personen gehen, die ueberhaupt Krebs bekommen kønnen (im Wesentlichen ist das im Konzept der „person-years at risk“ enthalten). Das bedeutet, wenn ein Mensch in einer Altersgruppe Krebs bekommt, dann faellt dieser aus der Statistik fuer die darauffolgenden Altersgruppen raus. Der Grund liegt darin, dass die zugehørigen „person-years at risk“ Null werden, sobald Krebs diagnostiziert wurde. Das bedeutet nicht, dass man stirbt, sondern nur, dass man nicht mehr zu den gefaehrdeten Personen gehørt. Das Konzept kann man sich leichter klar machen, wenn man sich Grippe anstatt Krebs denkt. Wenn man mit der Grippe durch ist, ist man immun, kann nicht mehr angesteckt werden und ist damit keinem Risiko mehr ausgesetzt.

Oder anders: die Wahrscheinlichkeit in einer gegebenen Altersgruppe Krebs zu bekommen ist _abhaengig_ (!) davon ob ich zur gefaehrdeten Personengruppe gehøre. Letzteres ist abhaengig (!) davon, ob ich bis hierhin „ueberlebt“ (also keinen Krebs bekommen) habe.
Ein Krebs-„Ereigniss“ in einer gegebenen Altersgruppe ist also abhaengig (!) davon, dass besagtes „Ereigniss“ nicht in einer vorhergehenden Altersgruppe auftrat.

Die Wahrscheinlichkeit eine gegebene Altersgruppe zu „ueberleben“ ist ganz einfach 100 % minus die Wahrscheinlichkeit, dass man Krebs bekommt. Das folgt aus dem zweiten Axiom von Kolmogorow: die Wahrscheinlichkeit fuer das sichere Ereigniss ist 100 % und das sichere Ereigniss ist in diesem Fall, dass ich Krebs bekomme oder nicht (also beide einzelnen Ereignisse zusammen genommen).
Weil es sich nun um voneinander abhaengige Ereignisse handelt, muss man die altergruppenspezifischen Ueberlebenswahrscheinlichkeiten miteinander multiplizieren, um heraus zu bekommen, ob man bis zu einer gegebenen Altersgruppe ueberlebt. Das korrigierte kumulative Risiko ist dann wieder nur 100 % minus die Ueberlebenswahrscheinlichkeit.

Diese Multiplikation der einzelnen Ueberlebens(!)wahrscheinlichkeiten (anstatt der Addition der einzelnen Krebs(!)wahrscheinlichkeiten wie im ersten Fall) ist mathematisch aequivalent zur „exponentiellen Abnahme der Anzahl der Menschen“ (die fuer die Statistik ueberhaupt in Betracht gezogen werden kønnen).

In der blauen Kurve im obigen Diagramm kommt also zum Ausdruck, dass man es eben gerade NICHT ohne Krebsdiagnose bis zur naechsten Altersgruppe geschafft hat, waehrend bei der lila Kurve davon ausgegangen wird (!), dass man von Datenpunkt zu Datenpunkt zu den „Ueberlebenden“ gehørt.

Ich weisz, ich weisz, statistische Aussagen (und wann welche Betrachtungsweise gewaehlt werden muss) kønnen knifflig sein. Aber ich wollte hier erklaert haben, warum ich weniger an der blauen, korrigierten Kurve und vielmehr an den Zahlen die zur lila,unkorrigierten Kurve fuehren, interessiert bin — das liegt an meiner Situation … … … und das soll nun wirklich genug sein fuer heute.