Søren in Norwegen

Weil zu viel abzuhandeln ist, knuepfe ich ohne viel Aufhebens direkt an das beim letzten Mal Besprochene an:

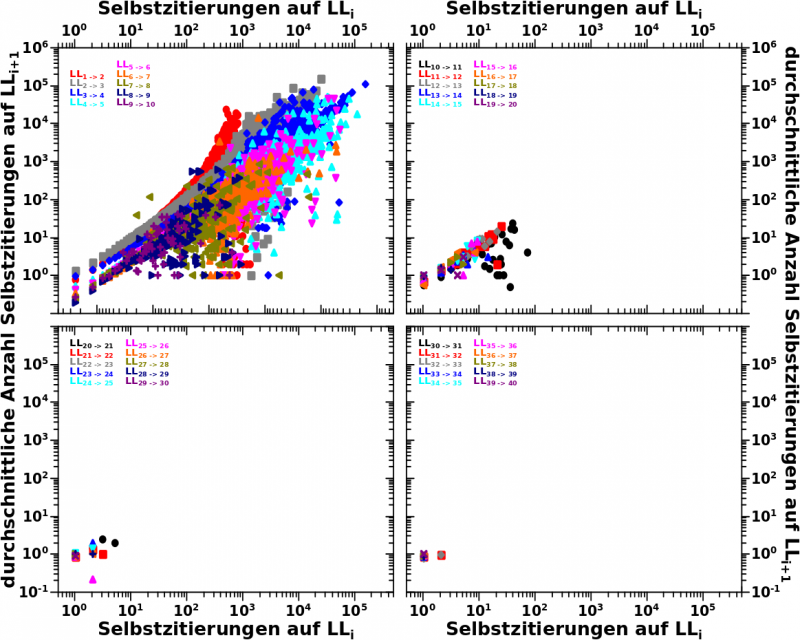
Pro Datensatz gilt das Folgende. Zunaechst wurde auf der Abzsisse abgetragen, wie viele Selbstreferenzen eine Seite auf einem gegebenen Linklevel i hat. Dann wurde fuer die selbe Seite geschaut, wieviele Selbstreferenzen diese auf dem naechsten Linklevel i + 1 hat. Dieser Wert wurde hier nicht abgetragen. Vielmehr bildete ich den Mittelwert der Selbstreferenzen auf Linklevel i + 1 fuer fuer _alle_ Seiten  die genausoviele Selbstrefenzen auf Linklevel i aufweisen wie die oben einzeln betrachtete Seite. Dieser Mittelwert ist auf der Ordinate abgetragen und ich diskutierte das beim letzten Mal genauer.

Dabei ist zu beachten, dass Seiten die auf einem Linklevel _keine_ Selbstreferenzen haben, NICHT weiter betrachtet wurden; ich behandle solche Seiten also als ob die bei diesem Linklevel „ausgestiegen“ sind. Dies gilt auch dann, wenn eine solche Seite auf einem høheren Linklevel wieder Selbstreferenzen aufweist. Eine eventuelle „Reaktivierung“ wird als irrelevant angenommen; empirisch ist das durchaus berechtigt, da es meist doch nur eine Selbstreferenz auf hohen Linkleveln gibt. Im Wesentlichen sieht man in diesem Diagrammen also nur Seiten, welche durchgehende „Ketten“ von Selbstreferenzen aufweisen.
In einem spaeteren Beitrag schau ich mir mal an, wie sich diese „Ausstiege“ und eventuelle „Reaktivierungen“ verhalten.

Damit hab ich gleich abgehandelt, warum im Wesentlichen ab LL₂₂ nix mehr zu sehen ist (und so weit geh ich auch nur deswegen, damit das konsistent mit dem hier Gezeigten ist). Es gibt nur wenige Seiten, die so lange durchgehende Ketten von Selbstreferenzen aufweisen.
Dennoch ist zu sehen, dass der beim letzten Mal erkannte Zusammenhang bzgl. der Anzahl der Selbstreferenzen offensichtlich fuer mehr als nur einen Linklevelschritt gilt. Und abgesehen von LL₁ zu LL₂ (die roten Punkte im ersten Diagramm); scheint dieser bei doppellogarithmischer Darstellung linear zu sein (was auch bereits beim letzten Mal zu sehen war).

Desweiteren sieht es so aus, als ob die Anstiege dieser Kurven (auch wenn es diskrete Punkte sind nennt man das so … denke ich) immer ungefaehr gleich sind … mhmm … wenn ich hier Pi mal Daumen schaue, dann scheint es so zu sein, dass ich von einem Linklevel zum naechsten so ganz grob ungefaehr 50 mal weniger Selbstreferenzen habe … interessant … das muss ich mal genauer auswerten.

Damit die lineare Regression schick aussieht, entfernte ich hierfuer an den Enden Punkte, behielt aber alle anderen Ausreiszer drin. Diesmal geh ich einen anderen Weg und mache zunaechst eine lineare Regression um dann alle Punkte zu entfernen, die mehr als einen festgelegten maximalen Wert von der Regressionsgeraden entfernt liegen (in Richtung der Ordinate). Den Prozess wiederhole ich so lange, bis keine Punkte mehr entfernt werden muessen.

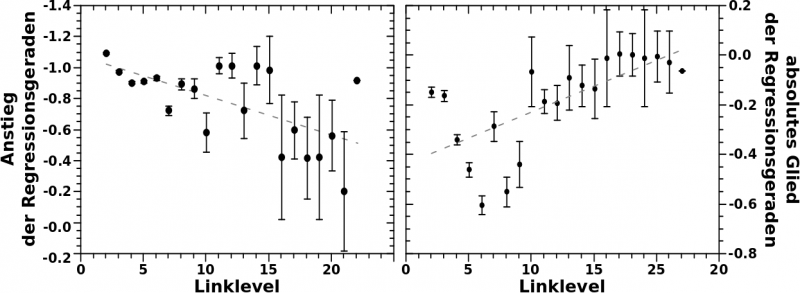
Das Ergebnisse bzgl. des Anstiegs und absoluten Glieds der Regressionsgeraden ist hier zu sehen (auszer fuer den Schritt von LL₁ zu LL₂) und …

… øhm … ich sag jetzt mal mehrdeutig.

Ich habe da zwar Regressionsgeraden rein gelegt, aber wichtige Punkte fallen mit dieser Geraden ueberhaupt nicht zusammen. Wichtige Punkte sind die bis ungefaehr LL₆ / LL₇, wo die Ausgangsdaten noch gut genug sind. Deswegen wuerde ich sagen, dass eine lineare Regression der Parameter der linearen Regressionen ueber die Datensaetze der obigen Diagramme die falsche Herangehensweise ist.
Nun kønnte ich da natuerlich eine Funktion durchpacken, welche diese Daten am Besten anpasst. Die Wahl einer Funktion sollte einen Zusammenhang mit einem plausiblen Mechanismus haben. Lineare, Potenz- und Exponentialfunktionen werden dafuer gern genommen. Dies weil sich so viel im Universum danach verhaelt und es meist durchaus plausibel ist erstmal anzunehmen, dass ein neues System sich auch danach verhaelt. Aber bei den Fehlerbalken kønnte ich irgendwas nehmen und das kønnte stimmen oder nicht.

Deswegen mache ich im Weiteren das, was man in solchen Faellen, wo man nicht weiter weisz, oft macht: ich versuche das (zukuenftige) Modell so einfach wie møglich zu halten. Das bedeutet dass ich einfach sage, dass sich alle obigen Kurven mittels linearer Gleichungen mit gleich bleibenden Regressionsparametern (gut genug) beschreiben lassen.
Den Anstieg setze ich dabei (nicht ganz so willkuerlich) fest auf 0.9. Dieser Wert ist im Wesentlichen nur aus den ersten sieben Punkten gewonnen (wo die Datenlage noch gut ist). Es ist ein Kompromiss der versucht einzubeziehen, dass der Anstieg zunaechst grøszer oder nahe eins ist, aber ja doch auch spaetere Daten erklaeren muss.
Fuer den Wert des absoluten Glieds habe ich den Mittelwert aller Punkte genommen (ca. -0.1469). Das fuehlt sich genauso richtig an wie irgend einen anderen Wert, beschreibt aber den Anfang wieder besser als andere Werte.

Somit weisz ich, wie sich das System von einem zum naechsten Linklevel entwickelt. Der Rest sollte nur vom Ausgangszustand abhaengig sein. Damit sollte ich beim naechsten Mal zur eigentlichen Simulation kommen kønnen und kann dann hoffentlich die erfolgreiche Berechnung der Verteilung der Selbstreferenzen pro Linklevel zeigen, wenn man nur die Verteilung dieser Grøsze im Anfangszustand kennt :)