Søren in Norwegen

Beim letzten Mal zeigte ich, dass sich die linklevelabhaengigen, individuellen Verteilungen der Selbstreferenzen bei doppellogarithmischer Darstellung mittels linearer Funktionen beschreiben lassen und dass der Anstieg der dazugehørenden (Regressions)Geraden zu nimmt. Nun wird es total spannend, denn ich werte heute die linklevelabhaengigen Parameter dieser linearen Funktionen aus.

Aber zunaechst zur Erinnerung: in den Diagrammen des letzten Beitrags stellte ich den Logarithmus eines Funktionswertes f(x) in Abhaengigkeit vom Logarithmus der Argumente x dar und erhalte eine Gerade. Die Formel fuer die Gerade sieht also so aus …

… mit dem Anstieg A und dem absoluten Glied B. Letzteres ist im Wesentlichen dafuer verantwortlich, wie grosz das Integral unter der Kurve wird, da dieser Parameter besagte Kurve nach oben oder unten schiebt.
Obige Gleichung ist aequivalent zu einem maechtigen Gesetz …

… und deswegen entspricht der Anstieg der Geraden in der doppellogarithmischen Darstellung dem Exponenten des Potenzgesetzes. Cool wa!

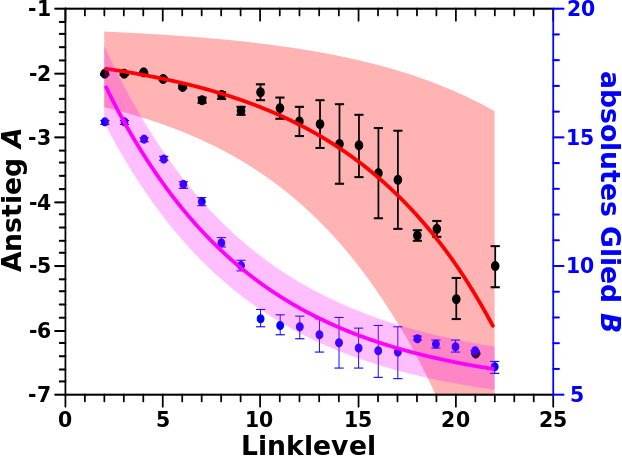
Soweit zur Wiederholung … nun schauen wir uns mal die Linklevelabhaengigkeit der Regressionsparameter in diesem høchst spannenden Diagramm an:

URST Cool wa! Jetzt hab ich schon zwei voll krasse Ergebnisse (hier ist das Erste) die ich so nicht erwartet haette. Krass deswegen, weil das hier auf zugrundeliegende Mechanismen hinweist, die ganz natuerlich in diesem Netzwerk entstanden sind. Aber genug der Schwaermerei darob solch schøner Resultate ich sollte erstmal sagen warum das so urst cool ist.

Sowohl die Linklevelabhaengigkeit des Ansteigs als auch des absoluten Glieds lassen sich am besten mittels einer Exponentialfunktion beschreiben. Diese hat im ersten Fall eine Zerfallskonstante von -7.76 und im zweiten Fall von +7.67 … … … Wait! What? … *nochmal kontrollier* … .oO(ja, das stimmt alles).

Die Wahl einer Exponentialfunktion zur Beschreibung der Daten kann natuerlich diskutiert werden. Aber weil ich nicht die geringste Ahnung habe, was oben erwaehnte Mechanismen sein kønnten, gehe ich erstmal von einfachen Dingen aus, was in diesem Fall zur Wahl einer Exponentialfunktion fuehrte.
Das sich das Vorzeichen zwischen den beiden Werte aendert liegt in der Natur der Sache. Der absolute Wert des Anstiegs der Geraden wird ja grøszer. Deswegen muss die Zerfallskonstante negativ sein, denn der Exponent eines exponentiellen Zerfalls enthaelt von sich aus ein Minus eins und das muss kompensiert werden. Das aendert nix an dem Gesagten. Wuerde man die Daten des einen Parameters an der Abzsisse spiegeln, waere das Vorzeichen beider Exponenten gleich.

Beide Zerfallskonstanten liegen (vom Vorzeichen abgesehen) total nah beieinander. Das weist darauf hin, dass die Linklevelabhaengigkeit beider Grøszen ein und dem selben Mechanismus zu Grunde liegen.

Es hatte einen Grund, warum ich beim letzten Mal dies schrieb:

[…] wenn die Werte der Datenpunkte der Grafen durch die Anzahl aller Wikipediaseiten geteilt wird, so erhaelt man die Wahrscheinlichkeit wie oft eine Seite so und so viele Zitate […] pro Linklevel erhaelt.
Das Integral ueber alle Daten und alle Linklevel ergibt […] die durchschnittliche Wahrscheinlichkeit ueberhaupt eine Selbstreferenz zu erhalten.

Wenn man in diesem Bild bleibt, so ist das absolute Glied obiger linearer Gleichung ein Ausdruck dessen was in dem zweiten Satz des Zitats steht. Je weiter fortgeschritten man im Linknetzwerk einer Seite ist, desto unwahrscheinlicher ist es eine Selbstreferenz zu erhalten … siehe der kleiner werdende Flaecheninhalt unter den beim letzten Mal gezeigten Grafen.
Ist es sinnvoll, dass diese Grøsze exponentiell abnimmt … mhmm … mein Bauchgefuehl sagt mir: durchaus.

Die Zunahme des (Betrags des) Anstiegs der Regressionsgeraden besagter Grafen sagt im Wesentlichen das Folgende aus: je weiter fortgeschritten man im Linknetzwerk einer Seite ist, desto unwahrscheinlicher ist es _mehr_ als eine Selbstreferenz zu erhalten.
Ist es sinnvoll, dass diese Grøsze exponentiell abnimmt … mhmm … mein Bauchgefuehl sagt mir auch hierbei: durchaus.

In beiden Faellen kommt das „durchaus“ meines Bauchgefuehls daher, dass høhere Linklevel bedeuten, dass sich die dort auftretenden Seiten thematisch mehr und mehr von der Ursprungsseite entfernen. Warum sollte Selbige also zitiert werden? Und diese Entfernung vom Ursprungsthema ist eben wirklich urst schnell … da kann ich auf den allererste Beitrag dieser Maxiserie verweisen, in dem ich erwaehne, dass es nur drei Schritte zwischen Trondheim und Kevin Bacon gibt … ich wuesste wirklich nicht, was diese beiden miteinander zu tun haben kønnten.
Wieauchimmer, dieser „Abstand“ nimmt im Bild des Linklevels zwar schrittweise (also linear) zu, aber der „thematische (!) Abstand“ dann wohl exponentiell. Das „urst schnell“ von weiter oben drueckt sich in dem hohen absoluten Wert der Zerfallskonstante aus … ein Exponent von (fast) 8 ist gigantisch! Mir ist kein einziges Naturgesetz mit einem so hohen Exponenten bekannt.

Eine weitere „Veranschaulichung“ des Gesagten sind die vielen Gespraeche, wo man „vom Hundertsten ins Tausendste kommt“ … weil es sich hierbei um einen Sprung um eine Grøszenordnung handelt, kann dieses Sprichwort durchaus als ein Ausdurck obiger Zustaende gesehen werden.
Somit entspricht die Zerfallskonstante dieser Parameter also in etwa wie stark sich die Themen der Seiten auf einem Linklevel vom Thema der Ursprungsseite entfernen. Das ist voll cool (!!!) denn damit gibt es einen mathematischen Ausdruck fuer ein sprachlich / psychologisch / soziales Phaenomen. Ich haette nicht gedacht, dass ich das ganz konkret und quantifizierbar in den Daten finden wuerde.

Das soll genug sein fuer heute. Zum Abschluss sei nur noch das Folgende erwaehnt: die Fehlerbalken der einzelnen Punkte kommen aus den Fehlern der Regressionsparameter (wie beim vorletzten Mal erwaehnt). Der Fehlerbereich der exponentiellen Funktion ist davon natuerlich unabhaengig.

Nachtrag:
Im obigen Bild ist mir ein Fehler unterlaufen. Das ist aber nicht so schlimm und aendert gar nichts an dem was ich schrieb und es handelt sich dabei um das Folgende. In der Formel am Anfang benutze ich den Logarithmus zur Basis 10. Dies deswegen, weil Diagramme wie beim letzten Mal logarithmische Skalen zur Basis 10 benutzen. Die Werte fuer das hier dargestellte Diagramm berechnete ich aber mit dem natuerlichen Logarithmus.
Fuer den Anstieg macht das ueberhaupt keinen Unterschied, der ist der Selbe, egal welche Basis man benutzt. Aber das absolute Glied ist bei Letzterem selbstverstaendlich grøszer als wenn die Basis 10 benutzt werden wuerde. Genaugenommen um einen (konstanten!) Faktor 2.30258 grøszer, welcher natuerlich das Reziproke des Logarithmus zur Basis 10 der Eulerschen Zahl ist. Mathematisch folgt das zwangslaeufig, denn letztlich muessen beide Formen die selben Daten beschreiben. Zur Kontrolle habe ich dennoch nochmals alle linearen Regressionen ausgefuehrt und kann sagen, dass dieser Faktor „experimentell“ bestaetigt wird … bis auf ein paar wenige Werte am Anfang und am Ende fuer die das aber plusminus innerhalb vertretbarer Grenzen auch gilt.
Weil es sich hierbei um einen konstanten Faktor handelt bleibt dann auch die Zerfallskonstante der Anpassung der Werte fuer B die Gleiche. Mit den gegebenen Datenpunkte erhalte ich einen Wert fuer Selbige von +7.22. Die Diskrepanz ergibt sich sich durch die „paar wenige[n] Werte am Anfang und am Ende“. Wenn ich diese kuenstlich „begradige“ so verschwindet die Diskrepanz ohne dass sich an der Position der Punkte im Diagramm grosz was aendert.
Mit den gegebenen Daten (und insb. aller Limitierungen die diese mit sich bringen) kann ich deswegen trotz des (relativ geringen) Unterschieds der Werte (welchen ich getrost in den so oft erwaehnten „10%-Fehler“ packen kann) weiterhin ohne schlechtes Gewissen vertreten, dass die Zerfallskonstanten fuer A und B im Wesentlichen gleich sind.