Søren in Norwegen

Beim letzten Mal zeigte ich zum Abschluss zwei repraesentative Verteilung der Selbstreferenzen pro Linklevel. Ich wollte damit darauf hinaus, dass diese Verteilungen sich ueber viele Linklevel nach einem maechtigen Gesetz verhalten. Bevor ich darauf beim naechsten Mal zurueck komme und das Ganze systematisch betrachte, møchte ich zunaechst mithilfe dieses Diagramms …

… auf zwei Sachen eingehen.

Die erste sind die wenigen Ausnahmen vom oben Gesagten. Naja, eigentlich sind es viele, aber die allermeisten der vielen Ausnahmen kønnen alle unter einer Kategorie zusammengefasst werden (und diese Kategorie liegt auch noch in der Natur der Sache) und deswegen zaehlen die alle zusammen nur als eine Ausnahme … aber vielleicht sollte ich einfach nur erklaeren.

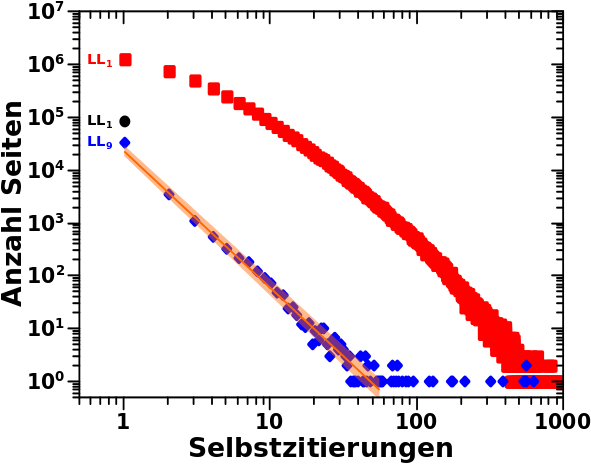
In dem Diagramm sehen wir die Verteilungen der Selbstzitate fuer LL₀ (schwarze Punkte), LL₁ (rote Quadrate) und LL₉ (blaue Diamanten). Wie immer bei diesen Verteilungen zaehlte ich (in diesem Fall) wieviele Seiten es gab (Ordinate), die auf dem gegebenen Linklevel so viele Selbstreferenzen erhielten, wie auf der Abzsisse angezeigt.
Nicht gezeigt sind die Punkte fuer null Selbstreferenzen; die sind naemlich im Wesentlichen fuer alles weitere unwichtig und lassen sich ohnehin nicht gut bei einer logarithmischen Achse darstellen..

Der erste Ausnahmefall ist LL₀. Dort sollte es ueberhaupt keine Selbstreferenzen geben (man ist ja noch keinen Schritt im Linknetzwerk voran geschritten). Wir wissen von frueher, dass der eine Punkt mit einem Wert von ca. 80k durch Artefakte zustande kommt.

Kurioserweise erlaubt mir dieses Artefakt den zweiten Ausnahmefall zu erklaeren, denn genau so sieht das auch aus, wenn man sehr weit im Linknetzwerk vorangeschritten ist. Dort liegt der Grund aber darin, dass dann die Chance fuer eine Selbstreferenz URST winzig ist. Entsprechend klein wird die „Signalstaerke“ und die Werte auf der Abzsisse liegen dann nur noch bei 1 (oder vielleicht mal 2) … also ich habe nur noch bei einer Selbstzitierung (und bei null) ein Signal.
Worauf ich hinaus will ist das Folgende: beim naechsten Mal interessiert mich der Anstieg der Verteilung in der doppellogarithmischen Darstellung (welcher dem Exponenten des Potenzgesetzes entspricht). Diesen erhalte ich durch lineare Regression; aber lineare Regression bei Werten die im Wesentlichen „Rauschen“ sind ist nicht sinnvoll.
Deswegen wuerde ich obige Aussage nur unter starkem Vorbehalt fuer als gueltig auf hohen Linkleveln ansehen. Vermutlich ja, aber die Daten geben das einfach nicht her.

Die dritte Ausnahme ist die Verteilung zu LL₁, diese verhaelt sich naemlich eindeutig nicht nach einem Potenzgesetz, denn selbst mit beiden Augen zudruecken kann ich die Daten da nicht mit einer linearen Funktion (bei doppellogarithmischer Darstellung) beschreiben. Das gilt bedingt mglw. auch fuer die Verteilungen bei LL₂ und LL₃, bei Letzteren kann ich aber auch mit gutem Gewissen eine Gerade durch relevante Abschnitte der Daten legen, die gilt halt nur nicht bei all zu kleinen Linkleveln.
Was passiert hier? Nun ja, das ist einfach zu erklaeren: von gaaaanz frueher wissen wir dass jede Ursprungsseite im Durchschnitt 30 (neue) Seiten auf LL₁ hat. Ja, auch von frueher wissen wir, dass es auch (Ursprungs)Seiten gibt, die deutlich mehr (oder weniger) als diese 30 Seiten auf LL₁ haben. Aber nach unten bin ich ohnehin begrenzt (weniger als null geht nicht) und nach oben liegt die Grenze bei so ca. 1000 Seiten … das ist zwar deutlich mehr, aber davon gibt es nur sehr wenige.

Wieauchimmer, von jeder Seite auf LL₁ kann die Ursprungsseite nur eine Selbstreferenz bekommen. Das limitiert wie weit eine Seite auf der Abszisse „reichen kann“; wenn ich nur 30 Seiten auf LL₁ habe, dann kann ich keine 31 Selbstreferenzen bekommen.
Ebenso sollte dies indirekt zu einer Ueberhøhung des Signals gegenueber einer Geraden (und damit einer konvexen Kruemmung der Daten) fuehren. Indirekt deswegen, weil das natuerlich nicht der Mechanismus ist, der zu besagter Ueberhøhung des Signals fuehrt. Vielmehr ist es so, dass ja gerade auf LL₁ sicherlich viele Seiten auf die Ursprungsseite zurueck verweisen, einfach weil das thematisch sehr oft nahe liegt. Ich habe also ohnehin schon ein høheres Signal und das „draengelt“ sich, durch ersteren Mechanismus, dann auch noch alles bei kleinen Werten auf der Abszisse.

So, genug zu den Ausnahmen.

Wichtiger fuer’s naechste Mal ist eigentlich alles zu LL₉. Da ist naemlich eine der oben erwaehnten Regressionsgeraden drin (die dicke orange Linie). Die sieht schick aus, nicht wahr; so richtig schøn mitten durch den (bei doppellogarithmischer Darstellung) linearen Teil der Daten.
Und hier liegt der Hase im Pfeffer! Denn ich habe ja rechts davon auch noch Daten … aber das sind nur ganz wenige, einzelne Seiten, die so viele Selbstreferenzen erhalten … und diese „passen“ ja offensichtlich nicht zu dem worauf ich hinaus will mit dem linearen Teil. Aber die wuerden natuerlich bei einer linearen Regression ueber alle Daten mit einebzogen werden und zu einer Gerade fuehren, die ueberhaupt nicht mehr „gut passt“.
Waehrend des Studiums  habe ich gelernt das zu ignorieren und das Lineal an den linearen Teil so anzulegen, dass die Linie richtig liegt und die Daten gut (genug) beschreibt … vulgo: schick aussieht … wenn ich den Anstieg und das absolute Glied einfach ablese (ohne was formal zu berechnen).
Und genau das habe ich fuer alle (relevanten) Verteilungen gemacht. Ich habe vom Ende (und wenn nøtig auch vom Anfang) so lange Punkte weggeschnitten, bis die Regressionsgerade schick aussah. Wie oben geschrieben, ist das kein schummeln, sondern wurde von Physikern schon immer so gemacht. Auszerdem ist das Potenzgesetz ohnehin nicht ueberall gueltig und der Bereich der Gueltigkeit ergibt sich daraus wo die Gerade die Daten gut beschreibt. Dennoch wollte ich den Prozess mal erwaehnt haben, denn letztlich habe ich die Geraden durch linere Regression erhalten.

Und damit bin ich dann auch bei der letzten Sache … dem orange-durchsichtigen Band um die dicke Linie. Bei der linearen Regression erhaelt man fuer die Parameter der Geraden einen „Fehler“ … vulgo: die plus/minus Werte … und das orange Band kennzeichnet diesen Bereich. Die Regressionsgerade kønnte also irgendwie liegen, solange es innerhalb dieses Bandes ist. Die wahrscheinlichste Gerade ist die eingezeichnete.
Beim naechsten Mal lasse ich die Baender weg, aber ich komme nochmal auf den „Fehler“ des Anstiegs zurueck. Deswegen wollte ich das hier mal erwaehnt haben.

So, das war jetzt viel mehr als ich urspruenglich dachte. Im naechsten Beitrag wird’s voll interessant :)