Søren in Norwegen

Vor einer ganzen Weile zeigte ich die Verteilung der Maxima der einzelnen Verteilungen der Selbstreferenzen. Aus einer Unstimmigkeit im allerersten Balken entwickelte ich in den letzten Artikeln in dieser Maxiserie das Konzept der (Wissens-)Archipele. Letzteres ist abgeschlossen und ich gehe nur nochmal ganz kurz auf die Verteilung der Maxima ein. Genauer interessieren mich die sieben „Ausreiszer“, die erst sehr spaet in ihrem Linknetzwerk zitiert werden.

Das war relativ einfach heraus zu bekommen und die erste Seite (jeweils einmal zitiert auf LL₂₆ und LL₂₇) gehørt zu Alpheus Harding. Mhmm … ja, viel weiter weisz ich dazu jetzt nicht zu sagen.
Auf LL₃₀ erhalten zwei Seiten ihre erste und einzige Zitierung: Estádio Luís Pereira und 1962 NCAA University Division baseball rankings. Weitere von diesen relativ obskuren Seiten, von denen mein „Favorit“ immer noch die bereits erwaehnte Bacon, Ohio ist.
Ebenso auf LL₃₀ zum ersten Mal zitiert wird William E. Livingston. Zunaechst kønnte man denken, dass es sich dabei im eine Person wie Alpheus Harding handelt. Interessant genug fuer einen eigenen Wikipediaeintrag, aber nicht bedeutend genug um einen „grøszeren Eindruck“ in der Weltgeschichte hinterlasse zu haben. Dieser erste Eindruck taeuscht aber, denn William E. Livingston erhaelt weitere Zitate auf LL₃₁, LL₃₂, LL₃₃, LL₃₆, LL₃₇, LL₃₉, LL₄₀, LL₄₅ und LL₅₀. Das kann nicht an seinen Kindern liegen, denn die werden nicht naementlich erwaehnt, ich nehme also an, dass die keine eigenen Wikipediaeintraege haben. An seiner Rolle als Offizieller der Stadt Lowell, Massachusetts kann es eigtl. auch nicht liegen. Diese wird naemlich sofort zitiert und alles was mehr oder weniger direkt damit in Verbindung steht sollte zu relativ fruehen Zitierungen fuehren. Mit dem was ich bisher ueber das Wikipedialinknetzwerk ausgewertet habe laeszt sich dies nicht løsen. Ich hoffe ich denke an diesen Mann, wenn ich so weit gekommen bin, dass ich es prinzipiell aufklaeren kønnte.

Als naechses folgt auf LL₃₅ und LL₃₇ Estádio Juca Ribeiro. Aha! … … … Øhm … ja … ich nehme an die Zitierungen erfolgen im Zusammenhang mit Fuszball.
Fuer die letzten zwei, ganz weit am Ende haengenden, Seiten Mitsubishi Yowa Sugamo Ground (zitiert auf LL₃₉) und Caius Novac gilt das bestimmt auch.

Vielmehr weisz ich dazu nicht zu sagen. Ich wollte nur mal schauen und hier steckt nix weiter drin was man lernen kønnte. Das liegt aber in der Natur singulaerer Ausreiszer.

… … …

… … …

… … …

Themenwechsel zu einem anderen losen Ende: die individuellen Verteilung(en) der Selbstreferenzen pro Linklevel steht noch aus

Zur Erinnerung: bei den totalen Links dachte ich zunaechst begeistert, dass sich dahinter was Cooles und Interessantes verbirgt, gestand am Ende dann aber doch ein, dass ich mich etwas verrant hatte. Das Selbe bei den neuen Links konnte ich kurz abhandeln.

Ich erwaehne das, weil ich nochmals kurz auf die Verteilung der Anzahl der Links pro Seite auf LL₀ (ob totale oder neue macht dabei keinen erwaehnenswerten Unterschied) zurueckkommen muss. Ganz spezifisch auf die Tatsaeche, dass diese Verteilung ueber ca. vier Grøszenordnungen (auf der Ordinate) einem maechtigen Gesetz zu folgen scheint. Das ist an und fuer sich nicht weiter verwunderlich, da viele Prozesse in der Natur Potenzgesetzen folgen.
Wichtig ist nun, dass dies auf høheren Linkleveln nicht mehr (oder nur noch sehr bedingt mit Augen zukneifen) gilt. Der Grund ist, weil dann ja auch die vielen Urpsrungsseiten die mit wenigen Links starteten so weit in ihrem Linknetzwerk gekommen sind, sodass immer irgendwie eine Seite mit vielen Links dabei ist. Das verschmiert also.

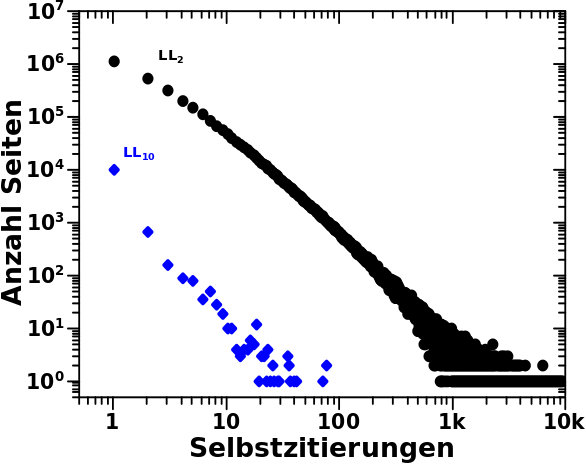
Nach dieser Wiederholung von bereits Bekannten war ich zunaechst ueberrascht, dass Letzteres nicht fuer die Selbstreferenzen gilt. In diesem Diagramm …

… sind zwei representative individuelle Verteilungen gezeigt. Um sinnvoll mehrere derartige Datensaetze darzustellen habe ich aus den bekannten Balkendiagrammen diesmal Punktdiagramme gemacht. Der Informationsinhalt ist natuerlich der Gleiche.

Wir sehen: egal ob LL₂ oder LL₁₀, so folgen die individuellen Verteilungen maechtigen Gesetzen.
Als ich etwas laenger darueber nachgedacht hatte, kam ich zu dem Schluss, dass ich eigentlich gar nicht ueberrascht sein musste. Denn auch wenn fuer die Verteilungen der (totalen/neuen) Links der oben erwaehnte „verschmierende Prozess“ einsetzt, so sind die Selbstreferenzen davon unabhaengig.
Klar, auf den ersten Linkleveln treten zunaechst mehr Selbstreferenzen auf, einfach weil mehr Seiten zur Verfuegung stehen. Das Integral unter der Kurve wird also grøszer und grøszere Werte auf der Abszisse werden „besetzt“. Ebenso klar ist, dass diese beiden Charakteristiken fuer høhere Linklevel abnehmen muessen (eben weil dann wieder weniger Seiten zur Verfuegung stehen). Und das sieht man in den beiden Kurven des Diagramms. Aber mir faellt kein Prozess ein, der zu Abweichungen vom Potenzgesetz fuehren kønnte.

Oder anders: die Verteilung der Grøsze der Einschlagskrater auf Mimas verhaelt sich ja schlieszlich auch nach dem gleichen maechtigen Gesetz wie die selbe Verteilung gemessen an Lady Luna. Es spielt ueberhaupt keine Rolle, dass Letztere einen ca. zehn Mal so groszen Radius hat im Vergleich zu Ersterem. Der Erdmond hat mit einer fast 100 Mal grøszeren Oberflaeche eine entsprechend høhere Anzahl an Kratern, das Signal welches besagte Verteilung ausmacht ist also grøszer … aber das verhaelt sich nach dem selben Potenzgesetz und insb. ist auch der Anstieg der Kurve fuer beide Verteilungen gleich.

Ich erwaehne den Anstieg deshalb, weil ich damit zu einer urst spannenden Sache ueberleiten kann. JA, egal wie hoch das Linklevel ist, die Verteilungen verhalten sich immer nach einem Potenzgesetz. ABER der Anstieg aendert sich.
Das waere aber zu viel des Guten fuer diesen einen Artikel und deswegen komme ich darauf beim naechsten Mal zurueck :) .