Søren in Norwegen

Die beim vorletzten Mal eingefuehrte Analogie, in der Wikipediaseiten angesehen werden wie Partikel eines idealen Gases, welche bei bestimmten „Temperaturen“ (Linklevel) bestimmte Zustaende (Anzahl der totalen Links) einnehmen kønnen, hilft mir beim naechsten Mal zwei Phasenuebergaenge dingfest zu machen.
Aber weil’s so wichtig ist, møchte ich heute darueber sprechen, dass ich die Daten die ich beim letzten Mal praesentiert habe, nicht einfach so nehmen kann, wie sie sind.  Der Grund ist (wie ich beim vorletzten Mal schrieb), dass ich […]

[…] die Zustaende zwischen dem kleinsten und dem grøszten besetzten Zustand einfach abzaehle und damit dann die Anzahl aller (plausiblen) Zustaende auf einem gegebenen Linklevel erhalte.

Es gibt aber in jeder Verteilung Zustaende die so weit weg sind vom Rest der Verteilung, dass die alles „kaputt“ machen. Oder anders: durch den Abstand eines einzigen Zustands vom Rest der Gruppe entstehen so viele leere plausible Zustaende, dass die aus der Anzahl aller plausiblen Zustaenden errechnten Ergebnisse nicht mehr sinnvoll sind.

Bei richtigen Messungen nennt man sowas „Ausreiszer“ und die dtsch. Wikipedia schreibt dazu:

[…] man [spricht] von einem Ausreißer, wenn ein Messwert […] allgemein nicht den Erwartungen entspricht.

Das ist korrekt, aber etwas zu spezifisch. Denn ich habe keine Erwartungen, oder vielmehr wiesz ich nicht, was ich erwarten soll. Denn trotz der Analogie sind die Wikipediaseiten eben doch kein ideales Gas, von dem ich erwarte, dass es sich auf bestimmte Art und Weise verhaelt. Entpsrechend habe ich keinen Erwartungswert um den rum ich eine gewisse Streuung der „Messwerte“ als normal ansehe und alles was auszerhalb des Bereiches faellt falsch sein muss.

Deswegen gefaellt mir (mal wieder) besser, was die englische Wikipedia schreibt:

[…] an outlier is a data point that differs significantly from other observations.

AHA! Das ist doch mal was. Mich duenkt, die dtsch. Wikipedia wollte das so sagen, aber die spezifischen Worte die gebraucht wurden druecken das nicht aus, wenn man mal naeher drueber nachdenkt.

Das hilft mir in diesem Fall zwar weiter, ist aber _zu_ diffus um irgendwas quantifizieren zu kønnen. Wo høren die validen Beobachtungen auf und wie signifikant ist signifikant? In der Praxis ist man da oft genug bei der Streuung um den Erwartungswert zurueck. Und das ist ja auch richtig so, denn das macht die Reproduzierbarkeit aus.

Es gibt ein paar mathematische Tests fuer Ausreiszer. Leider bauen diese wieder darauf auf, dass man etwas erwartet. Also entweder verteilt sich (wieder) alles um einen (oder mehrere) Erwartungswert(e) oder, dass bei „wilden“ Verteilungen (bspw. mit mehreren Maxima oder Verteilungen die sich aus mehreren Normalverteilungen zusammen setzen etc. pp.) die mathematische Beschreibung der besagten Verteilung bekannt ist.
Die Verteilungsfunktion der Zustaende der Wikipediaseiten ist mir nicht bekannt und veraendert sich im gegebenen Fall auch von Linklevel zu Linklevel. Und was sind die Erwartungswerte, wenn sich die Zustaende ueber mehrere Grøszenordnungen erstrecken?
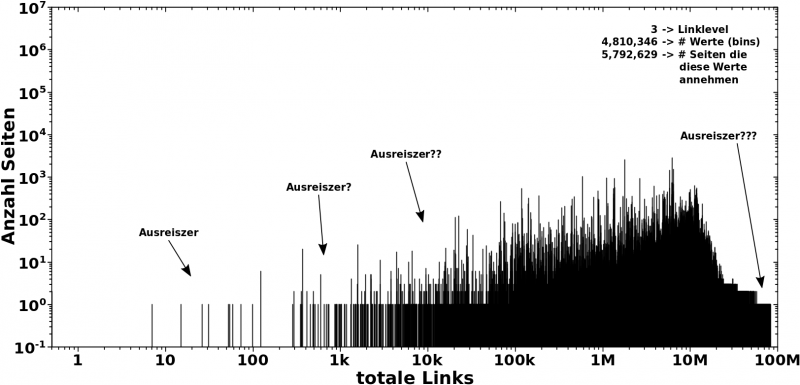
Im Wesentliche stehe ich vor dem „Das-sieht-ma-doch“-Problem, was sich aber mathematisch nicht klar ausdruecken laeszt. Als Beispiel zur Illustration nehme man die Verteilung der Zustaende auf LL₃:

Die paar Zustaende ganz links, zwischen Werten von 7 und ca. 120 totalen Links, sind eindeutig Ausreiszer … das sieht man doch. Aber was ist mit den Werten zwischen ca. 180 und 100 totalen Links? Die sehen ja aus, als ob die schon noch dicht genug an den anderen Observationen liegen. Andererseits ist das ’ne logarithmische Achse und das ist sicher OK die als Ausreiszer zu definieren.
Mhmm … wenn ich das so sage, was ist denn dann mit den Zustanden zwischen 10-tausend und ich sag jetzt mal ca. 50-tausend totalen Links? Das Maximum der Verteilung liegt eindeutig bei ca. 10 Millionen totalen Links, das ist ganz schøn weit weg.
Und dann die Zustaende zum Ende der Verteilung! Aufgrund der logarithmischen Komprimierung sehen die zwar aus wie ganz dich am Rest, aber da gibt es bei lineraer Achse sicherlich deutlich grøszere Leerraeume als bei den ganz eindeutigen Ausreiszern ganz am Anfang. Sind Letztere dann vielleicht doch keine Ausreiszer?

Wie man sieht ist das alles nicht so einfach. In meiner zweiten Doktorarbeit habe ich mich damit professionell herumgeschlagen. Leider kann die dort entwickelte Methode der Detektierung (und Korrigierung) von Ausreiszern, wenn man nicht weisz was man erwarten soll, hier nicht angewendet werden.

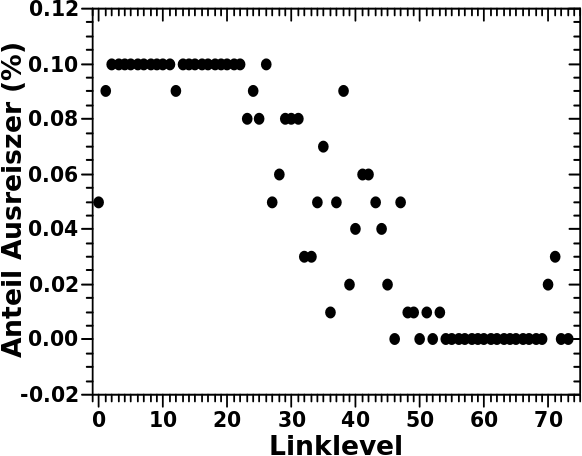
Deswegen bin ich dann doch darauf zurueckgefallen, dass ich die jeweils ersten und letzten 0.05 % aller Zustaende einfach abschneide (insgesamt schlieszt das 0.1 % aller Zustaende aus).
Aber Achtung das sind Maximalwerte und in den meisten Faellen schliesze ich weniger Zustaende aus:

Der Grund ist, dass ich einen mehrfach besetzten Zustand nicht aufteile in „gut“ und „schlecht“. Alle Seiten („Partikel“) in diesem Zutand sind gleichwertig. Oder anders: sollte die Ausschlieszungsgrenze von 0.05 % in die Mitte eines mehrfach besetzten Zustandes fallen, dann werden vielmehr alle Seiten die in diesem Zustand sind als „gut“ gewertet und in den auszuwertenden Datensatz uebernommen.

Der Gebrauch des Wertes 0.1 % bedeutet, dass (bei ca. 6 Millionen Seiten) an beiden Enden im Extremfall ca. 3000 Zustaende ausgeschlossen werden.
Ich gebe zu, dass ich mich entschied 0.1 % als Kriterium bzgl. des Ausschlieszens von Ausreiszern zu nehmen, weil ich einen praktikablen Kompromiss finden musste, zwischen „aesthetischen Gruenden“ und dem Wunsch so viele Daten wie møglich hinzuzunehmen. Wobei Ersteres dominierte, weil ich bei diesem Wert die Phasen (deren Vorhandensein zwar vermutet wird, aber der Nachweis noch ausstand; bzw. in dieser Reihe noch aussteht) besser unterscheiden kann.
Man sieht aber alles bereits deutlich, wenn man nur 30 Zustaende an den Enden wegschneidet. Ja selbst wenn ich nur die 3 aeuszersten Werte ausschliesze, treten die entscheidenden Merkmale bereits sichtbar hervor. Und wenn man weisz wonach man sucht, sieht man es auch im kompletten Datensatz … aber das war ja das Problem, ich wusste zunaechst nicht so richtig wonach ich suche, wie sich das in den Daten ausdrueckt und wo das konkret ist … selbst wenn ich Vermutungen diezbezueglich hatte.

Trotz aller Rhe­to­rik bzgl. der Integritaet der Wissenschaft(ler) ist diese Herangehensweise insb. in den sog. „angewandten Wissenschaften“ sehr weit verbreitet. Daran ist erstmal nix auszusetzen, solange das ordentlich diskutiert wird und Ergebnisse nicht pløtzlich verschwinden, wenn man die Daten anders „aufbereitet“. Leider passiert Ersteres so weit ich weisz nie und Letzteres vermutlich (deutlich) øfter als uns lieb ist … *seufz*. … Und auch wenn ich oben explizit die sog. „angewandten Wissenschaften“ erwaehne, ist das im Groszen und Ganzen in allen (Teil)Gebieten der Wissenschaft so … mit ein paar Ausnahmen, wie bspw. die Hochenergiephysik oder (heutzutage) einige (viele?) groszangelegte klinische Studien, die mehr und øfter vorregistriert werden … wobei das auch nicht immer hilft, am Ende doch noch was „schick zu machen“, damit das imponierender bei der Publizierung aussieht.

Das soll genug sein fuer heute, beim naechsten Mal gibt’s dann endlich „Butter bei die Fische“.