Søren in Norwegen

Beim letzten Mal zeigte ich die Verteilungen der totalen Links fuer jedes Linklevel und ich teilte alles in 4 Abschnitte ein. Ich erwaehnte auch, dass der Uebergang von Abschnitt drei zu Abschnitt vier total krass ist, und dass es wie ein Phasenuebergang aussieht, wenn der „Wald der Balken“ sich so pløtzlich massiv lichtet.

Aber warum erinnerte mich das an einen Phasenuebergang? Und was ist das ueberhaupt? Und was fuer „Phasen“ sollen denn Wikipediaseiten annehmen? Und wie sollen Wikipediaseiten von einer „Phase“ in eine andere „Phase“ wechseln?

Nun ja, ich dachte dabei zunaechst an die Bildung von Cooper-Paaren oder ein Bose-Einstein-Kondensat. Aber beide diese Effekte kenne ich nur rein phaenomenologisch (bzw. ist mein Verstehen der Gleichungen bzgl. der Cooper-Paarbildung mittlerweile 20 Jahre her).
Deswegen ein anderes Beispiel, von dem ich hoffe, dass es zu mehr Klarheit beitraegt: unterkuehltes Wasser, das pløtzlich gefriert. Etwas bildlicher: in fluessiger Form kann ein Wassermolekuel viele Geschwindigkeiten (und Orte) annehmen, pløtzlich gefriert dann alles und in der festen Form nehmen alle Molekuele nur noch eine einzige Geschwindigkeit an (sie stehen dann still). Das ist ein Phasenuebergang von der fluessigen Phase zur festen Phase. Meist geschieht der nur nicht so pløtzlich.
Ein kurzes und schønes Video bzgl. des oben erwaehnten Bose-Einstein-Kondensats zeigt was ich meine … wobei ich zugebe, dass der allerletzte Schritt im Video fuer Nicht-Physiker vermutlich eher esoterisch erscheinen mag … ok ich gebe es zu, auch fuer Physiker erscheint das bestimmt esoterisch.
Aber ich greife hier eigentlich vor, denn das ist genau das, worueber der heutige Artikel geht.

Wieauchimmer, dass das wie ein Phasenuebergang aussieht, hat mir mein Bauchgefuehl im Wesentlichen sofort gesagt. Danach beschaeftige mich das tagelang und ich habe etliche Stunden mit der Analyse und dem Schreiben von Programmen (zur Analyse) verbracht. Letzteres, weil ich eine Grøsze oder Eigenschaft der Verteilungen finden wollte, welche mir erlaubt dieses Bauchgefuehl zu testen. Denn bei einem Phasenuebergang verhalten sich bestimmte, ein System beschreibende Grøszen charakteristisch.

Zunaechst verfolgte ich einen Ansatz, bei dem ich die „Dichte des Balkenwaldes“ untersuchte. Das brachte mich aber weder bei linearer Definition noch bei logarithmischer Definition eines „Volumens“ (Abschnitt auf der Abzsisse) weiter. Die Idee mit der Dichte ging aber schon in die richtige Richtung … und dann fiel es mir auf! Mensch! Auf LL₀ scheint die Verteilung der Links eine gewisse Aehnlichkeit aufzuweisen, mit der Verteilung die meine unfaire Muenze vor ein paar Jahren produzierte! Letztere war eine Maxwell-Boltzmann Verteilung und der Zusammenhang damit brachte mich auf den richtigen Weg, wie ich einen Phasenuebergang nachweisen kønnte. Aber der Reihe nach.

Die Maxwell-Boltzmann Verteilung wurde urspruenglich „erfunden“ um bei einer gegebenen Temperatur die Geschwindigkeitsverteilung der Partikel eines idealen Gases zu beschreiben.
Man denke sich wieder das Beispiel von Wasser, nur dieses Mal nicht unterkuehlt, sondern mit einer Temperatur von 101 Grad Celsius (bei Normaldruck) und somit in der Form von Wasserdampf. Ein Wassermolekuel kann von sehr langsam bis sehr schnell viele Geschwindigkeitszustaende annehmen. Die Maxwell-Boltzmann Verteilung beschreibt nun, wie wahrscheinlich es ist, dass ein Molekuel sich in einem bestimmten Geschwindigkeitszustand befindet. Bei gerade mal 101 Grad Celsius sind die meisten Molekuele relativ langsam und ein paar sind sehr schnell. Die Wahrscheinlichkeit ein Molekuel zu finden welches sehr sehr sehr sehr schnell ist, ist im Wesentlichen Null.

Jetzt verandere ich die Temperatur dieses Systems in mehreren Schritten … und in Gedanken.

Zuerst heize ich den Wasserdampf immer weiter auf. In einem geschlossenen Gefaesz steigt dann der Druck. Der Druck ist aber im Wesentlichen die Kraft, mit der die Wassermolekuele gegen die Wand pressen. Da sich die Masse der Molekuele nicht aendert muss die (mittlere) Geschwindigkeit der Molekuele zunehmen, wenn bei steigender Temperatur der Druck steigt. Das bedeutet, dass sich das Maximum der Verteilung zu høheren Geschwindigkeitszustaenden verschiebt. Auszerdem wird die Verteilung breiter. Das bedeutet, dass bei steigender Temperatur die Wahrscheinlichkeit ein sehr sehr sehr sehr schnelles Teilchen zu finden (deutlich) zunimmt. Gleichzeitig nimmt die Wahrscheinlichkeit ein sehr langsames Molekuel zu finden ab.

Im naechsten Schritt kuehle ich den Wasserdampf wieder ab. Die im letzten Paragraphen beschriebenen Dinge gehen zunaechst „rueckwaerts“ und wenn ich zu 100 Grad Celsius (und darunter) abkuehle, passiert etwas „Seltsames“ — ein Phasenuebergang. Die Wassermolekuele klumpen sich zusammen, sie kondensieren aus der gasførmigen in die fluessige Phase.
In der fluessige Phase sind die møglichen Zustaende fuer ein Wassermolekuel stark begrenzt. Sowohl was die Geschwindigkeit, als auch den Ort belangt. Die Verteilung wird also deutlich schmaler, einfach schon aus dem Grund, weil ich keine sehr (sehr sehr sehr) schnellen Teilchen mehr finden kann.
Nichtsdestotrotz ist das Maximum der Verteilung immer noch bei relativ hohen Geschwindigkeiten. Wie jeder aus eigener Erfahrung weisz, ist frisch gebruehter Tee ziemlich heisz. Das bedeutet dann aber, dass die mittlere Geschwindigkeit der Wassermolekuele (trotz aller Einschraenkungen) immer noch relativ hoch ist.
Ach ja, die Geschwindigkeitsverteilung von fluessigem Wasser wird nicht mehr durch die Maxwell-Boltzmann Verteilung beschrieben, aber das ist nicht so wichtig, denn eine Geschwindigkeitsverteilung ist es immer noch.

Nun kuehle ich noch weiterab. Das Maximum de Geschwindigkeitsverteilung „wandert“ zu immer kleineren Geschwindigkeiten und bei Null Grad Celsius gefriert das fluessige Wasser zu Eis. Dies ist ein weiterer Phasenuebergang, der die møglichen Zustaende der Wassermolekuele nochmals massiv einschraenkt. Unter bestimmten Umstaenden kann Wasser sich deutlich unter den Gefrierpunkt abkuehlen, ohne dass es zur Eisbildung kommt, bis dann ganz pløtzlich alle Molekuele auf einmal die Phase wechseln — und damit bin ich bei dem was ich oben erwaehnte.

So, ihr meine lieben Leserinnen und Leser seid ja aufmerksam und denkt mit. Deswegen seid ihr bestimmt selber drauf gekommen, dass die obigen vier Paragraphen, und was ich da ueber die Geschwindigkeitsverteilung der Wassermolekuele bei den verschiedenen Temperaturen sage, uebertragen werden kann auf die vier Abschnitte bei der Verteilung der Anzahl der totalen Links Seite und Linklevel vom letzten Mal! … Krass wa!

Das ist natuerlich der Grund, warum ich das beim letzten Mal so detailliert aufgeschrieben habe. Selbstverstaendlich ist die Analogie nicht perfekt, aber mir geht es auch nur im die Idee, dass die Partikel eines gegebenen Systems mit einer bestimmten Wahrscheinlichkeit gewisse Zustaende einnehmen kønnen. Die Wahrscheinlichkeit fuer manche Zustaende ist grøszer (oder kleiner) als fuer andere und wenn ich die Parameter des Systems veraendere, dann aendern sich die Wahrscheinlichkeiten, dass die Partikel gewisse Zustaende annehmen.

Im gegebenen Fall sind die „Partikel“ die individuellen Seiten, die „Temperatur“ ist das Linklevel und der „Zustand“ die ein „Partikel“ bei einer gegebenen „Temperatur“ annehmen kann, ist die Anzahl der totalen Links. Wenn ich nun die Anzahl der Zustaende weisz und wie diese besetzt sind, dann kann ich damit andere Sachen berechnen und letztlich auch Hinweise fuer Phasenuebergange finden.

Soweit zur Analogie. Das Problem ist nun aber, dass, anders als bei einer Maxwell-Boltzmann Verteilung, die Wahrscheinlichkeiten der Zustaende auf einem gegebenen Linklevel keinem (mir) bekannten mathematischen Gesetz folgt. Pragmatisch wie ich bin, benutze ich (wie so oft) einen phaenomenologischen Ansatz und nehme eben diese Daten um mehr ueber die Zustaende und deren Verteilung heraus zu finden.

Das bedeutet das Folgende.
Zunaechst einmal nehme ich an, dass die Statistik gut ist. Bei fast 6 Millionen „Partikeln“ ist diese Annahme durchaus gerechtfertigt.
Desweiteren nehme ich an, dass alle Zustaende die das System (also die Gesamtheit aller „Partikel“) auf einem gegebenen Linklevel annehmen kann, im Wesentlichen auch angenommen werden. Das bedeuet NICHT, dass jeder Zustand auch von (mindestens) einem Partikel angenommen wird. Es bedeutet aber, dass sich die Balken in den Verteilungen (mehr oder weniger) ueber den gesamten „Zustandsraum“ verteilen. Oder anders: zwischen dem ersten und letzten Zustand kønnen durchaus grøszere Luecken sein, aber vor dem ersten Zustand und hinter dem letzten Zustand ist dann auch wirklich nix; bzw. sind dort die Wahrscheinlichkeiten, dass ein Zustand dort angenommen wird so klein, dass diese nicht betrachtet werden muessen.
Als Beispiel nehme man die Verteilungen von Abschnitt 3 vom letzten Mal. Die Balken der Verteilung sind alle in einem kleinen Bereich und dass ich die nur dort sehe bedeutet dann, dass die Zustaende auszerhalb dieses Bereichs auch nicht angenommen werden kønnen, unter den gegebenen Umstaenden.
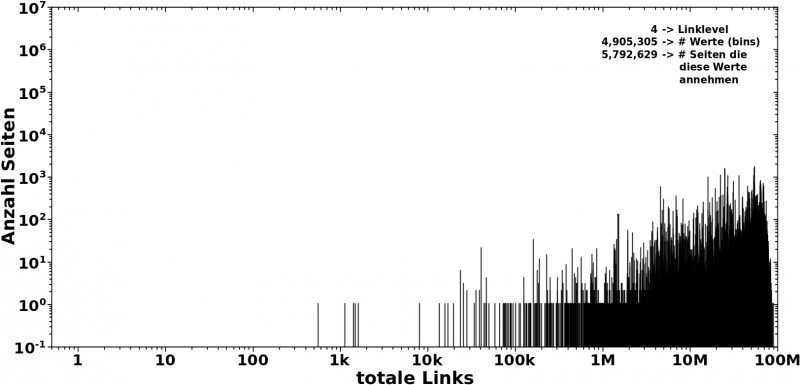
Im Gegensatz dazu die Verteilung bei LL₄:

Das Meiste spielt sich zwischen ca. 5 Millionen und ca. 80 Millionen ab. Aber die Verteilung hat Auslaufer bis ca. 1k mit unbesetzten Luecken dazwischen.

Das ist eine sehr wichtige Sache, denn wie oben geschrieben, will ich ja wissen, wie viele Zustaende ich habe und wie diese bestzt sind. Aber wie komme ich auf die Anzahl ALLER (plausiblen) Zustaende? Bei Maxwell-Boltzmann kann ich die einfach aus der mathematischen Funktion berechnen und dann sagen, dass bspw. ab einer Wahrscheinlichkeit von 10^-6 die Besetzung nicht mehr plausibel ist und ich alle Zustaende mit kleinerer Wahrscheinlichkeit nicht mehr mit zur Anzahl aller Zustaende dazurechne.
Hier aber sehe ich, dass ich bis zu ca. 90 Millionen Links haben kann (bei „hohen Temperaturen“). Ich kann nun aber die Anzahl der møglichen Links in der „heiszen, fluessigen Phase“ im besagten Abschnitt 3 nicht bis 90 Millionen ausdehnen. Dass ein solcher Zustand angenommen wird, ist nicht plausibel. Dito bzgl. all zu kleinen Zahlen der totalen Links bei „erhøhten Temperaturen“.
Die Løsung des Problems liegt in obiger (innerhalb gewisser Grenzen durchaus gerechtfertigter) Annahme. Praktisch bedeutet das, dass ich die Zustaende zwischen dem kleinsten und dem grøszten besetzten Zustand einfach abzaehle und damit dann die Anzahl aller (plausiblen) Zustaende auf einem gegebenen Linklevel erhalte.

Wenn ich die Anzahl aller møglichen (plausiblen) Zustaende habe, zaehle ich ab, welche Zustaende tatsaechlich besetzt sind. Damit kønnte ich dann eine Entropie berechnen. Ich weisz aber nicht, ob ich damit auch was sehe.
Desweiteren schaue ich, in welchen Zustaenden sich die Majoritaet der „Partikel“ befindet. Befindet sich die Majoritaet in nur ein paar wenigen der møglichen Zustaende, kønnte es sich um ein Gruppenphaenomen, bspw. das „ausfrieren“ in einen „festen Zustand“, handeln.
Auszerdem untersuche ich dann noch, wieviele „Partikel“ sich einsam und allein in ihrem Zustand aufhalten (oder vielleicht auch mal zu zweit oder zu dritt, je nach „Phase“ oder so), oder ob sie sich mit anderen „Partikeln“ zusammen tun. Der Unterschied zum Obigen liegt darin, dass hier immer noch relativ viele Zustaende besetzt sind, aber mit mehreren „Partikeln“ (bspw. 5 oder 23 oder 523 oder so). Das ist dann also kein Gruppenphaenomen.
Und letztlich kønnte ich als Ausreiszer all jene Zustaende definieren, die sich bspw. nicht innerhalb des Gebietes befinden, in dem (bspw.) 90 % aller besetzten Zustaende sind. Aber da bin ich unsicher, ob ich das auch machen werde. Naja, ich werde mir das schon mal anschauen, aber wenn es schønere Ergebnisse gibt, wenn ich die Ausreiszer drin lasse, dann lasse ich die drin … denn dann sind sie ja per Definition keine Ausreiszer mehr sondern gehøren zum ordentlichen Datensatz.

Aber auf all dies muesst ihr, meine lieben Leserinnen und Leser, euch noch gedulden. Dieser Artikel hier ist naemlich schon lang genug.

Ach so, der Grund, warum mich die oben erwaehnte „Dichte des Balkenwaldes“ auf den richtigen Weg fuehrte (selbst wenn der konkrete Ansatz erfolglos war) ist, dass ich bei Anzahl der møglichen und tatsaechlich besetzten Zustaende an die Zustandsdichte in der Festkørperphysik dachte; diese ist naemlich …

[…] the proportion of states that are to be occupied by the system at each energy.

Hier kam mir also (mal wieder) mein Hintergrundwissen in der Physik zugute. Das Studium hat sich also (mal wieder) voll gelohnt :) .

Im Weiteren betrachte ich KEINE Zustandsdichte(n) nach der formalen Definition in der Festkørperphysik. Aber ich werde die im letzten Paragraphen erwaehnten „Messgrøszen“ in Bezug setzen zur Anzahl aller møglichen Zustaende und das wir ja dann auch so eine Art „Dichte“.
Den Titel behalte ich bei, weil der so schøn zeigt, aus wie vielen Quellen Inspiration kommt, die dann zur Løsung (mehr oder weniger) komplexer Fragestellungen fuehrt :) … Toll wa! So ist’s eben in der Wissenschaft und Forschung :) .