Søren in Norwegen

Uff … da steht ein (A) im Titel … das bedeutet dann immer, dass ein Kapitel dieser Serie aus mehreren Unterkapiteln besteht. In diesem Fall steht am Ende eine echt coole Sache, aber ich brauche eine Weile um alles zu erklaeren, damit man das am Ende versteht. Ich selber habe mir einige Tage den Kopf drueber zerbrechen muessen, bevor ich eine Idee hatte was ich da eigentlich sehe und wie ich das testen kønnte. Aber der Reihe nach.

Vor ein paar Monden zeigte ich die Verteilung der Links pro Wikipediatitel. Vor nicht so langer Zeit stellte ich die Verteilung der totalen Links pro Linklevel vor. Die zwei Sachen haengen natuerlich zusammen; Ersteres ist die Verteilung der totalen Links auf LL₀. Ich machte mir dann mal die Arbeit und schaute mir diese Grøsze fuer ALLE Linklevel an.
Zusammen ergab das 74 Verteilungen … und die werde ich euch alle zeigen. Aber (ich hoffe) auf eine Art und Weise, die es euch, meinen lieben Leserinnen und Lesern, erspart, 74 Diagramme einzeln anzuschauen — naemlich als animiertes PNG.

Genug der langen Vorrede; so sieht die Entwicklung der individuellen Verteilungen der totalen Links pro Linklevel aus:

Hier gibt es so einiges zu diskutieren. Heute beschraenke ich mich darauf, das Obige in verschiedene Abschnitte einzuteilen. Zunaechst aber eine kurze Erklaerung, was man hier sieht.

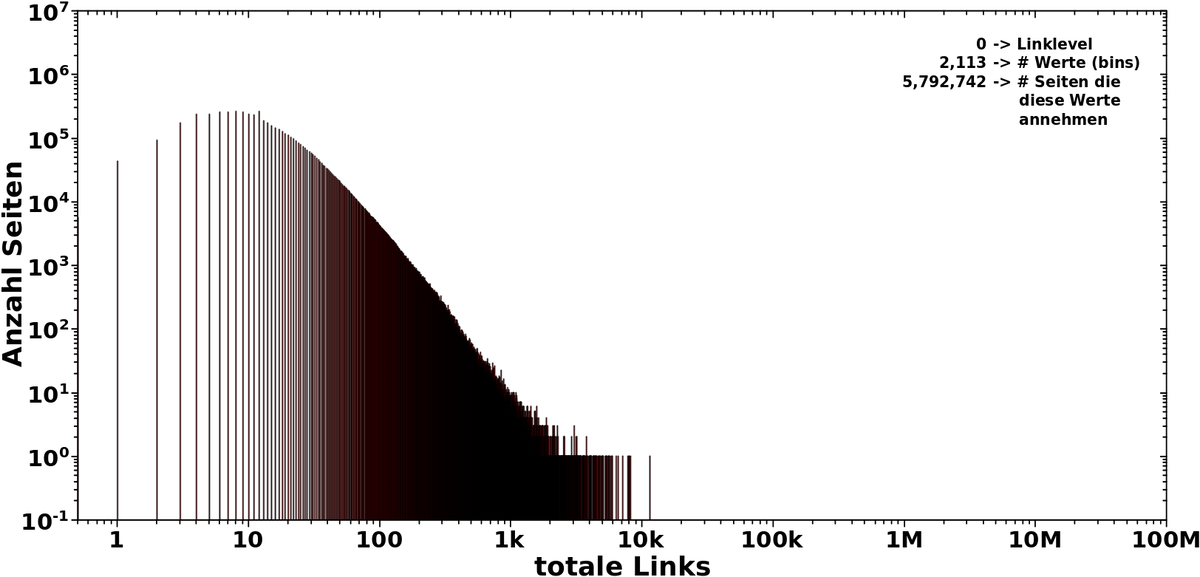
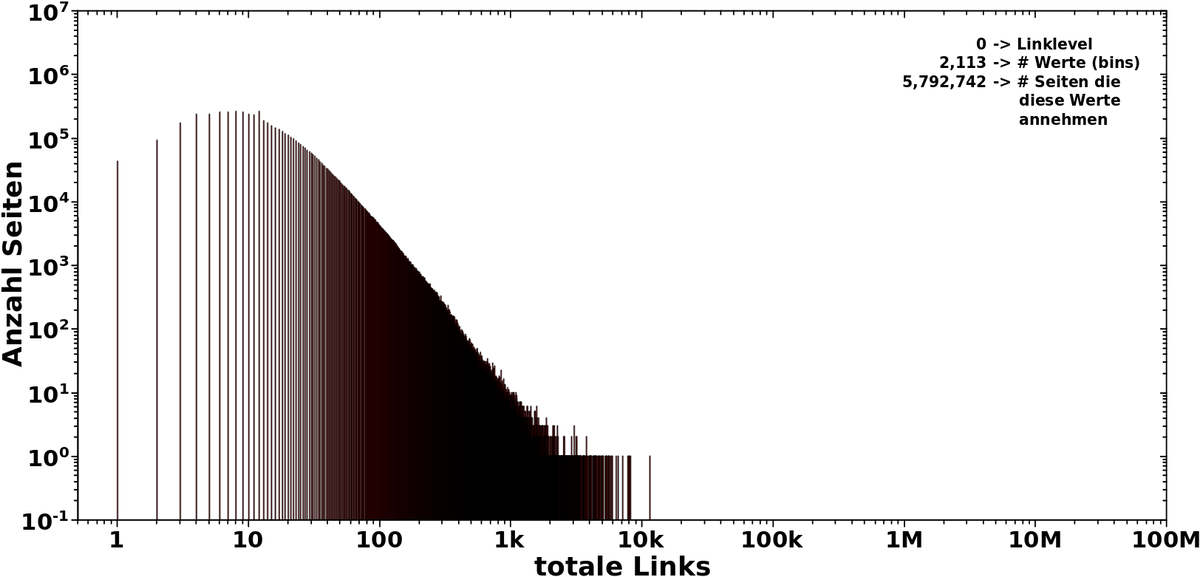
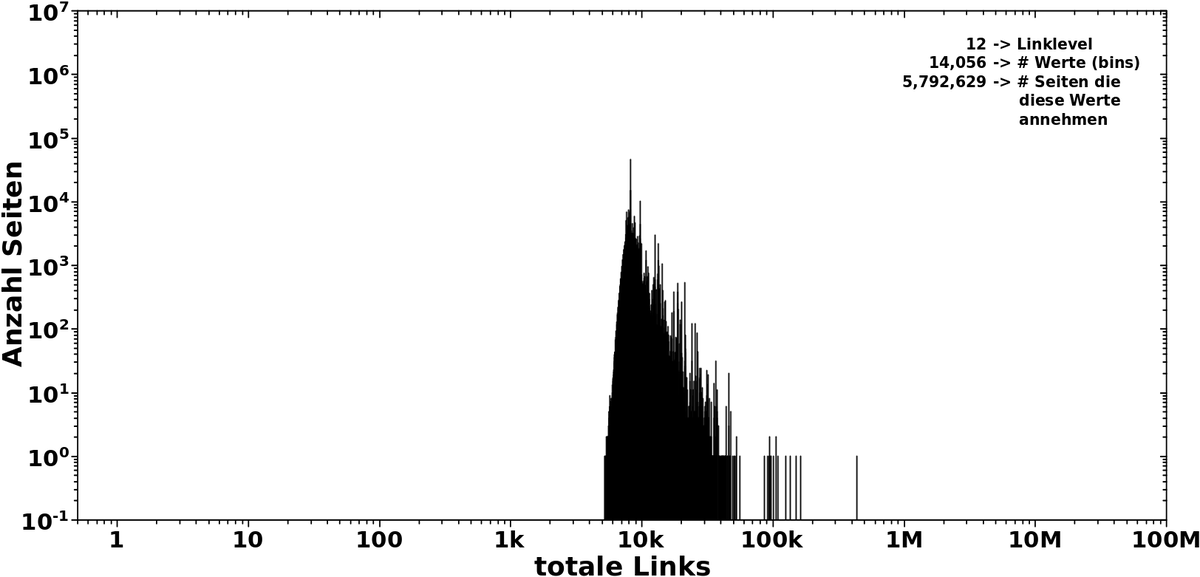
Auf jedem Linklevel hat eine Seite eine bestimmte Anzahl totaler Links. Diese Anzahl ist auf der Abzsisse abgetragen. Die Ordinate ist dann eine Art „Zaehler“, der zaehlt, wie viele Seiten diese totale Anzahl Links auf dem gegebenen Linklevel hat.
Oben rechts gebe ich in jedem Diagramm an, wie viele Werte auf dem gegebenen Linklevel auftreten. Dabei ist der Wert „null“ herausgenommen, denn das ist ja, wenn in den allermeisten Faellen eine Seite auf dem Linklevel davor keine neuen Links mehr hatte und deshalb gar nicht bis hierher gekommen ist. In einem Histogramm werden oft viele Werte in einem Behaelter (engl.: bin) zusammengefasst. Aufgrund der logarithmischen Achse nehme ich keine solche Zusammenfassung vor; oder anders: „bins“ haben die „Laenge eins“ (es passt nur ein Wert rein).
Desweiteren kann die Anzahl der Werte niemals grøszer sein als die Anzahl der (noch vorhandenen) Seiten. Desweiteren gebe ich die Anzahl der Seiten an, welche diese Werte annehmen. Diese Zahl ist wiederum ohne die Seiten, die auf dem gegebenen Linklevel null totale Links haben.

Jaja, das was ich da schrieb ist eben eine ganz normale Verteilung. Ich schreibe das aber dieses Mal extra auf, weil das Verstaendniss dessen was man in den Diagrammen sieht, so wichtig ist fuer das was spaeter noch kommt.
Aber nun soll es losgehen mit dem ersten Abschnitt.

Diesen wuerde ich einteilen vom Start bis zum Maximum der Gesamtverteilung, also von LL₀ bis LL₅:

Der erste Abschnitt ist dadurch gekennzeichnet, dass die Anzahl der Werte auf der Abzsisse drastisch zunimmt. Auch wenn ich das nicht explizit sagte, so konnte man das indirekt durch die Betrachtung der Gesamtverteilung „erahnen“.
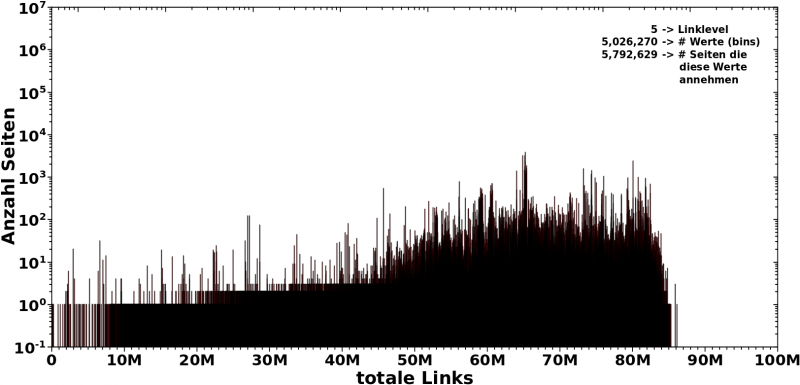
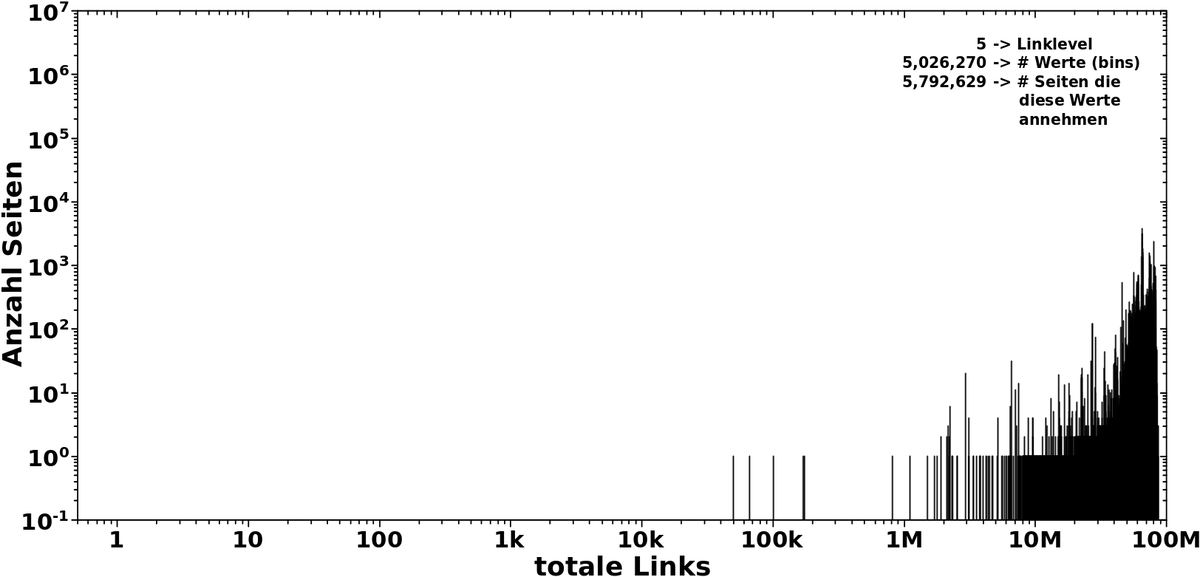
Bei LL₅ scheint sich alles an die „Wand“ zu draengen, aber dem ist mitnichten so! Das ist wieder die logarithmische Komprimierung, die ich frueher bereits erwaehnte. Bei linearer Abzsisse sieht man, …

…, wie lang sich die Verteilung tatsaechlich hinzieht und wieviel Platz der (im obigen Bild winzig kleine) weisze Bereich von 90 Millionen bis 100 Millionen eigentlich „verbraucht“. Oder anders: die erste Beschriftung bei linearer Abzsisse — „10M“ — wird auf LL₀ und LL₁ nicht mal erreicht und gerade so ueberschritten bei LL₂. Dennoch nehmen diese Bereiche bei logarithmischer Achse sehr viel Platz ein. Das ist sehr wichtig, das immer im Hinterkopf zu haben.

Man beachte auch das schwarze Band am unteren Rand. Dieses wird gebildet durch die vielen einzelnen Seiten, die als einzige eine gewisse Anzahl totaler Links haben. Die Balken stehen hier so dicht, dass diese das besagtes  Band bilden. Auch das wird spaeter nochmal wichtig.

Charakterstisch fuer Abschnitt eins ist somit die drastische Zunahme der angenommenen Werte (der totalen Links) von Linklevel zu Linklevel, diese Werte werden aber zunehmend (und bei LL₅ hauptsaechlich) von nur einer Seite angenommen.

Abschnitt zwei wurde ich einteilen von LL₆ bis ungefaehr LL₁₂:

Ich habe hier LL₅ dringelassen, als bessere Orientierung bzgl. des Uebergangs von Abschnitt 1 zu Abschnitt 2.

Abschnitt 2 ist zum Einen dadurch gekennzeichnet, dass die Anzahl der Werte wieder abnimmt. Auch das ist bereits (indirekt) durch die Betrachtung der Gesamtverteilung bekannt.
Das andere Kennzeichen kann ich nicht wirklich quantifizieren, aber „man sieht es doch!“ … oder besser: qualitativ zeichnet sich Abschnitt 2 auch dadurch aus, dass die Verteilung noch ueber einen relativ groszen Bereich geht (bei logarithmischer Achse). Aber zum Ende hin draengen sich die Werte auf der logarithmischen Achse in einen immer kleineren Bereich.

Quantitativ ist das natuerlich logisch, zwischen 1k und 10k passen nunmal nur 9k Werte waehrend zwischen 1M und 10M neun Millionen Werte passen. Aber „logarithmisch gesehen“ nimmt LL₈ drei „Bereiche“ auf der Abzisse ein (von ca. 100k bis 100M), waehrend LL₁₂ (ohne die Ausreiszer ganz rechts) nur knapp einen „Bereich“ einnimmt.
Mein Bauchgefuehl sagte mir, dass hier was ist. Aber eben weil ich das zunaechst nicht direkt in konkrete Zahlen fassen konnte, brauchte ich ein paar Tage um das was das Bauchgefuehl erkannt hat, auch wirklich aufzuspueren. Aber ich greife vor.

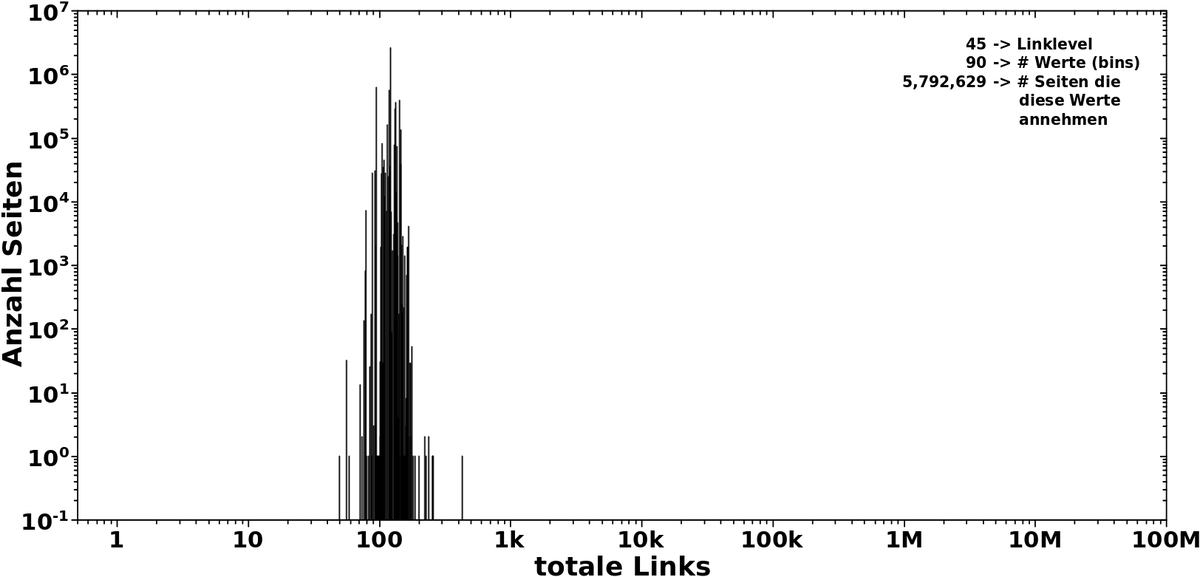
Abschnitt 3 wuerde ich nun von ungefaehr LL₁₃ bis ungefaehr LL₄₅ einteilen. Dieser Abschnitt zeichnet sich dadurch aus, dass die angenommenen Werte ungefaehr einen halben Bereich auf der Abzsisse einnehmen …

… (ich weisz, ich weisz, das klingt jetzt nicht gerade sehr wissenschaftlich). Ebenso verschiebt sich das Maximum der Verteilung langsam zu niedrigen Zahlen. Auch hier nimmt die Anzahl der angenommen Werte ab, aber laengst nicht mehr so drastisch wie in den vorherigen zwei Abschnitten. Aber es faellt auf, und ist ein weiteres Kennzeichen dieses Abschnitts, dass die Amplitude des Maximums stetig zunimmt. Von ein paar Zehntausend zu mehreren hundertausend und in einigen Faellen sogar in den Millionenbereich.
Das bedeutet, dass immer mehr Seiten ein und denselben Wert bei der Anzahl der totalen Links haben. Zum einen ergibt sich das zwingend, denn zwischen 100 und 1k liegen nunmal nur 900 Werte. Aber eine Gleichverteilung von ca. 6 Millionen Seiten, wuerde eine Amplitude von ca. 7-tausend ergeben. Hier geht also immer noch was vor und mein Bauchgefuehl sagt mir, dass das der gleiche Prozess ist, den ich bereits zum Ende von Abschnitt 2 erwaehnte.

Nun zum abschlieszenden Abschnitt 4 von LL₄₆ bis LL₇₃. Hier passiert etwas Seltsames und mein Bauchgefuehl sagt mir, dass das eine andere Sache ist, als in der vorherigen Abschnitten — die Verteilung nimmt immer noch ca. einen halben Bereich auf der Abzsisse ein …

… aber der „Wald der Balken“ lichtet sich massiv. Das heiszt, dass alle Seiten zum Ende ihrer Linkkette (mehr oder weniger) die selbe Anzahl totaler Links haben. Das kønnten durchaus die Saisons des São Paulo FC sein, wie bereits beim letzten Mal spekuliert. Aber auch hier sagt mir mein Bauchgefuehl, dass da noch mehr zu holen ist.

Mhmm … der vorhergehende Paragraph schafft es nicht im Geringsten auszudruecken, warum mir das so „komisch“ vorkam, dass mich das tagelang beschaeftige und ich etliche Stunden an Analyse und Programme schreiben (zur Analyse) dafuer benutzte. Ich sag’s mal so: DAS IST KRASS WAS HIER PASSIERT! Das sieht naemlich aus wie’n Phasenuebergang! Aber was fuer eine Phase haben denn Wikipediaseiten (bzw. die Anzahl der Links) und wie sollen die in eine andere Phase uebergehen?
Ich sagte ja, dass dies ziemlich krass und super spannend ist. Ich komme darauf an anderer Stelle zurueck.

Eigentlich gibt es noch einen abschlieszende Abschnitt, den ich aber mit in Abschnitt 4 gepackt habe. Das ist ganz am Ende, wenn ab ungefaehr LL_67/68 die allermeisten Seiten „aussteigen“. Das ist ein so gewaltiger separater Prozess, welcher die Effekte aller anderen Prozesse komplett ueberdeckt. Weil das so offensichtlich ist und beim letzten Mal bereits diskutiert wurde, schreibe ich da nix weiter zu.

Das soll genug sein fuer heute. Der Beitrag ist (unter anderem durch die groszen Bilder) relativ lang geworden. Aber eigentlich ist das hier nicht all zu schwer zu verstehen. Ich schrieb im Wesentlichen ja nur die Beobachtungen nieder und spekuliere ein bisschen.

In den naechsten Beitraegen versuche ich den im Text erwaehnten Prozessen auf den Grund zu kommen. Aber vielmehr sei noch nicht verraten. Nur zwei Bemerkungen zum Abschluss. Zum Einen habe ich die Beobachtungen so detailliert niedergeschrieben, weil das Verstaendniss derselbigen wichtig ist fuer das was noch kommt. Zum Zweiten sind die hier erwaehnten Abschnitte mehr oder weniger willkuerlich und rein phaenomenologisch gewaehlt. Diese Abschnitte muessen modifiziert werden um die zugrundeliegenden Prozesse besser in Worte fassen zu kønnen.

Genug!