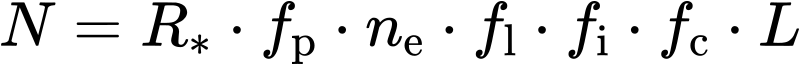Søren in Norwegen

Beim letzten Mal erwaehnte ich, dass fuer die Parameter der Drake-Gleichung derartig unterschiedliche Werte geschaetzt werden, dass man da urst krass verschiedene Resultate heraus bekommt. Das geht von einem leeren Universum (von uns mal abgesehen) bis zu so vielen auszerirdischen Zivilisationen, dass die sich fast schon gegenseitig auf die Fuesze treten. Die Literatur (meist die populaere, aber oft genug auch die wissenschaftliche) tendiert zu Letzterem — und das ist ja das Fermi Paradoxon.

Nun ist es aber so, dass bei der Berechnung von N, der Anzahl der Zivilisationen in unserer Galaxis, immer punktgenaue Werte fuer die Parameter genommen werden. Manchmal nehmen die Autoren dann noch andere (punktgenaue) Werte um zu zeigen wie unsicher die Rechnung ist. Das løst dann zwar nicht das Paradoxon, soll aber als ein Ausdruck fuer unser (wissenschaftliches) Unwissen angesehen werden. Und das ist eigentlich auch genau der richtige Weg … nur ist das nicht die richtige Herangehensweise, denn ein paar Werte in einer Gleichung zu aendern ist nicht systematisch.

Sandberg, A., Drexler, E. und Ord, T. (hiernach nur als SDO abgekuerzt) schauten sich unser Unwissen bzgl. der Parameter deswegen mal sytematisch an und meiner Meinung nach ist der Titel ihres Artikels mit „Dissolving the Fermi Paradox“ recht passend gewaehlt … wenn auch etwas provozierend, aber mich duenkt, dass das kalkuliert war (Wortspielkasse).
Als eine Nebenbemerkung: ich weisz nicht, wie ich arXiv-Artikel zitieren soll, auszer, dass ich den Link setze (in welchem die DOI steht fuer den Fall, dass der Link mal stirbt).

Aber der Reihe nach. SDO argumentieren, dass wir nicht nur irgendwelche zufaelligen Werte in die Drake-Gleichung einsetzen kønnen um irgendwas „zu zeigen“. Vielmehr sollten alle bisher publizierten Werte fuer die Parameter in ihrer Gesamtheit betrachtet werden. Dann ist der Unterschied in diesen Werten ein Ausdruck fuer unsere (wissenschaftliche) Unsicherheit. In den (zum Artikel) zusaetzlichen Dateien gibt es eine Tabelle, in der SDO alle (wissenschaftlichen) Quellen fuer die Parameter angeben, die sie finden konnten. Und die Unterschiede kønnen schon gewaltig sein. So gehen bspw. die Abschaetzungen fuer die durchschnittliche Lebensdauer einer Zivilisation von 45 Jahren bis 1 Milliarde Jahre. Oder die Werte bzgl. des Anteils der Planeten in der habitablen Zone mit Leben geht von 10^-30 (!) bis 1. Ersteres ist echt urst krass klein, aber Letzteres bedeutet, dass Leben im Wesentlichen garantiert ist auf jedem Planeten der sich dafuer eignet. Andere Parameter hingegen haben eine viel kleinere Unsicherheit; die Schaetzungen der Sternentstehungsrate liegt bspw. zwischen 1 und 50 Sternen pro Jahr.

Das sind aber nur die Extremwerte. In viele Abschaetzungen findet man sehr aehnliche Werte fuer die Parameter. Das ist dann natuerlich Ausdruck fuer eine gewisse (wissenschaftliche) „Sicherheit“. Nicht unbedingt im Sinne von vorhandenen Messungen (die ohnehin nicht durchgefuehrt werden kønnen) aber im Sinne der Abschaetzungen eines Spock die Captain Kirk den sicheren Fakten anderer vorzieht. Nehmen wir bspw. nochmals die Werte fuer die Entstehung von Leben. Der extrem kleine Wert von 10^-30 wird nur ein Mal angegeben. Hingegen wird in 17 Faellen abgeschaetzt, dass die Entstehung von Leben (beinahe) garantiert ist. Und dann natuerlich die Werte dazwischen.

In der Statistik spricht man von Sachen wie Varianz, Mittelwert und Median einer Verteilung. Man beachte, dass, abhaengig von der Art der Verteilung, solche Werte nicht immer angegeben oder gar definiert werden kønnen. Aber die Werte der Parameter der Drake-Gleichung sind logarithmisch normalverteilt (das bedeutet, dass der Logarithmus der Werte genommen wird und dann sind diese (logarithmierten) Werte normalverteilt) und da ist das alles kein Problem.
Damit kann man dann aber stochastische Modelle erstellen, in denen unsere Unsicherheit modelliert werden kann und wie sich das auf N auswirkt.

Was mit „unsicherheit modellieren“ gemeint ist, møchte ich eine mehr intuitive Erklaerung des Prozesses geben (um dann die rigorose statistische Modellierung SOD zu ueberlassen).

Wir wissen nicht, welche Werte fuer die Paramter „richtig“ sind. Und wie oben erwaehnt werden dann oft ganz andere Werte genommen, welche ein  vøllig unterschiedliches Resultat zur Folge haben. Dieses wird dann im Umkehrschluss angesehen als „Beweis“, dass die Drake Gleichung nicht brauchbar ist.
Was aber, wenn wir nicht nur eine Rechnung, sondern eine Million Rechnungen machen? Und jedes Mal waehlen wir aus allen publizierten Werten (inklusive derjenigen die mehrfach auftauchen!) zufaellig aus, welcher denn fuer eine gegebene Rechnung benutzt werden soll. Dieser Prozess des „zufaelligen Ziehens“ von (publizierten) Werten modelliert auf eine gewisse Weise unsere Unsicherheit bzgl. der Parameter. Und weil wir das eine Million mal machen, kønnen wir statistische Aussagen ueber unsere Unsicherheit bzgl. N modellieren. Ich komme darauf nochmal zurueck, weil ich ja noch den Bogen kriegen muss, warum dies das Paradoxon aufløst.

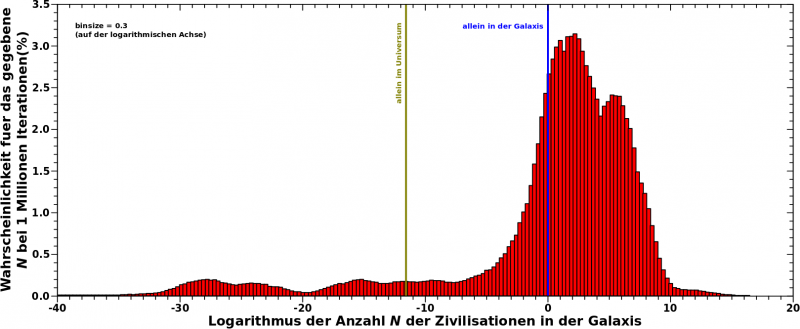
Das habe ich mal gemacht und die Frage war dann: wie oft erhalten wir mittels dieser Methode „vertraute“ Resultate fuer N und wie oft Werte die ein leeres Universum bedeuten? Das Ergbniss meiner Rechnungen sieht man hier:

Man beachte, dass die Abzsisse logarithmisch ist. Sonst benutze ich die nicht-logarithmischen Werte (in diesem Fall fuer N) um die Achse zu beschriften und variiere den Abstand der kleinen Teilstriche entsprechend. Dieses mal benutze ich den logarithmierten Wert, also den Exponenten der Grøszenordnung des Wertes (vulgo, das „hoch y“ in „x mal zehn hoch y“). Von Strich zu Strich steigert sich der Wert von N also um einen Faktor zehn (!) auch wenn das linear aussieht!
Ich musste das so machen, weil es sonst nicht so schick ausgesehen haette, denn ich wollte das Ausmasz zeigen, ueber wie viele Grøszenordnungen sich N strecken kann. Und eigentlich geht das noch 15 Grøszenordnungen runter, denn die kleinsten Werten haben einen Exponenten von -65.

Das Maximum dieser Verteilung (jaja … da ist noch ein Nebenbuckel aber ich irgnoriere den mal) liegt bei 100 Zivilisationen in der Galaxis. Sehr haeufig erhaelt man sogar deutlich høhere Werte; bspw. eine Million oder gar eine Milliarde Zivilisationen in unserer Galaxis. Zunachst kønnte man da denken, dass das dann doch genau wieder das Fermi Paradoxon ist und in dem Sinne stimmt das auch, aber dann ignoriert man das, was Links des Peaks ist.

Die blaue Linie bei 10⁰ markiert unsere (einzige) „Messung“: eine Zivilisation in unserer Galaxis. Und man sieht, dass die Wahrscheinlichkeit dort und auch bei Werten noch weiter links davon erstaunlich hoch ist. Geht man noch weiter zur (oliv)gruenen Linie, dann sind wir schon bei einem komplett leeren (observierbaren) Universum.

Kurze Abschweifung: New Horizons hat nicht nur ein paar Bilder vom Pluto gemacht (auch wenn mir scheint, dass dies das Einzige ist, was in der Øffentlichkeit wahrgenommen wird), sondern hat neben der Kamera auch noch ein paar andere Messinstrumente fuer uns mitgenommen. Eines davon hat gemessen, wie dunkel das Weltall denn eigentlich ist.
Das ist wichtig, denn in der Umgebung der Erde kann man das nicht machen. Hier gibt es total viel Staub und deswegen „glitzert und blinkert“ das auf allen Bildern von Messinstrumenten in der Naehe der Sonne (Naehe muss in diesem Satz gesamtsonnensystemtechnisch interpretiert werden). Das fuehrt dann dazu, dass man ganz schwache, weit entfernte Galaxien nicht sehen kann, weil die schwaecher leuchten als das „glitzern und blinken“. Aber wenn man weisz, wie stark das „glitzern und blinken“ ist, dann kann man aus der Anzahl der weit entfernten Galaxien die wir sehen abschaetzen, wie viele Galaxien wir nicht sehen kønnen.
Vor ein paar Jahren haben das mal ein paar Leute gemacht und die kamen zu dem Schluss, dass wir ca. 90 % der Galaxien nicht sehen. Die geschaetzte Zahl aller Galaxien im Universum lag dann (plusminus) bei 2 mal 10 hoch 12.
New Horizons hat nun, fern abseits des „Glitters“ im inneren Sonnensystems, festgestellt, dass das Universum deutlich dunkler ist als erwartet. Das wiederum bedeutet, dass es deutlich weniger unentdeckte Galaxien gibt. Man nimmt jetzt an, dass nur ungefaehr die Haelfte aller Galaxien nicht gesehen werden kønnen. Damit nimmt die Anzahl aller Galaxien im Universum um eine Grøszenordnung auf (plusminus) ca. 2 mal 10 hoch 11 ab.
Aber genug der Abschweifungen. Ich wollte nur kurz sagen wo der Wert des (oliv)gruenen Striches herkommt, weil das coole Wissenschaft (Wortspielkasse) ist.

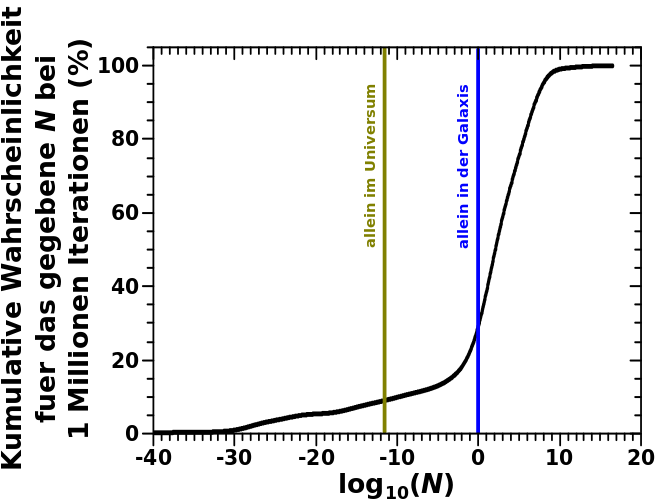
Jedenfalls sehen wir im obigen Histogramm, dass selbst bei der (oliv)gruenen Linie noch ein betraechtliches „Signal“ ist! Die kumulative Wahrscheinlichkeit verdeutlicht besser, was dieses „Signal“ eigentlich bedeutet:

Die hier zu sehende Kurve stellt dar, wie grosz die Wahrscheinlichkeit ist, ein N zu erhalten welches kleiner oder gleich dem Wert auf der Abzisse ist. Man summiert also alle individuellen Wahrscheinlichkeiten (die einzelnen Balken im Histogramm) bis zu dem gegebenen N auf.

Wenn wir nun den Wert bei N = 10⁰ ablesen, so erhalten wir eine kumulative Wahrscheinlichkeit von fast 31 %. So weit, so gut, aber was bedeutet das eigentlich? … Dafuer muss ich etwas weiter ausholen.

Um es gleich zu sagen: dieses Resultat bedeutet NICHT, dass wir mit einer Wahrscheinlichkeit von 31 % allein sind in unserer Galaxis.
Aber wie oben erwaehnt kennen wir die genauen Werte fuer die Parameter der Drake-Gleichung nicht. Unsere Unsicherheit drueckt sich in den verschiedenen (publizierten) Werten aus. Einige werden sicher naeher an der Wahrheit liegen als andere. Aber das wissen wir eben nicht. Bei den 1 Million Berechnungen wurde diese Unsicherheit „implementiert“, indem Werte zufaellig ausgewaehlt wurden und das hat das oben praesentierte Histogramm zur Folge.
Die kumulative Wahrscheinlichkeit (die ja aus dem Histogramm folgt) sagt uns nun, dass bei unserem derzeitgen Wissensstand, oder vielmehr bei unserer derzeitigen Unsicherheit bzgl. der Parameter, wir uns nicht wundern sollten, dass wir keine galaktischen Nachbarn sehen … oder høren? … aber Radiowellen sind ja auch nur elektromagnetische Wellen, also ist „Sehen“ gar nicht so verkehrt. Wieauchimmer, Letzteres ist die „Fermi Beobachtung“ und diese liegt absolut innerhalb dessen was zu erwarten ist, bei adaequater Betrachtung unserer Unsicherheiten.
Im Wesentlichen ist das das gleiche Argument, warum Physiker zehn Fantastilliarden Messungen machen bevor wir  eine Entdeckung verkuenden. Selbst dann, wenn nach der 23. Messungen schon klar ist, was man vor sich hat. Eben um den „Raum der Møglichkeiten“ weiter einzuschraenken — oder anders: um unsere Unsicherheiten kleiner zu machen.

Aber mich duenkt SDO druecken das besser aus (alle Hervorhebungen von mir):

[…] this conclusion does not mean that we are alone (in our galaxy or observable universe), just that this is very scientifically plausible and should not surprise us. It is a statement about our state of knowledge, rather than a new measurement.

Und das ist dann auch die Aufløsung des Paradoxons! Denn …

[t]he Fermi observation […] provides only very weak evidence about whether we will soon go extinct or whether interstellar communication or travel is impossible.

Die Fermi Beobachtung ist unser (einziger) Messwert, der im Zusammenhang mit punktgenauen Angaben fuer die Parameter der Drake-Gleichung oft als Paradoxon interpretiert wird. Und dieses Paradoxon wird oft genug maximal fatalistisch interpretiert. Nur die Interpretation als Paradoxon ist bereits falsch, denn wenn man die Unsicherheiten ordentlich mit einbezieht, dann ist das ueberhaupt kein Paradoxon. Vielmehr ist die Fermi Beobachtung einfach nur eine weitere, gar nicht mal so unwahrscheinliche Møglichkeit in Raum aller Møglichkeiten. Oder anders (und wieder besser) in den Worten von SDO:

While using point-estimates in the Drake equation frequently generates estimates of N that would produce a Fermi paradox, this is just an artefact of the overconfidence implicit in treating them as having no uncertainty.

Und das finde ich natuerlich ziemlich knorke, wenn wir nicht alle garantiert sterben muessen.

Die obigen Berechnungen sind nur eine ganz krude Implementierung unserer Unsicherheit in die Diskussion rund um die Ergebnisse der Drake-Gleichung. SDO haben das dann noch rigoros mathematisch behandelt und kommen (bei unserem derzeitigen (Un)Wissensstand) auf gar noch deutlich høhere Wahrscheinlichkeiten, fuer das keiner-da-zum-spielen-Szenario.

Wobei zu sagen ist, dass diese Erkentniss nicht an und fuer sich neu ist. Im wissenschaftlichen (im Gegensatz zum populaeren) Diskurs wurde die Møglichkeit dass N = 1 ist immer als ein wahrscheinliches Resultat akzeptiert.

Zum Abschluss des Artikels møchte ich dann noch sagen, dass das obige Ergebniss auch komplett anders interpretiert werden kann: (sehr) grosze Werte liegen mit guten Wahrscheinlichkeiten innerhalb des Møglichkeitraumes und wir sollten absolut Lauschen ob einer unserer Nachbarn „Hallo“ sagt :)

Eigentlich wollte ich was ueber die Normalverteilung schreiben und wie das mit dem Fortschreiten der Menschheit in eine ganz wunderbare Zukunft zu tun hat.

Dummerweise geht das nur, wenn man ueber die Anzahl wirklich intelligenter Menschen redet. Selbstverstaendlich tragen alle Maedchen und Jungs, Maenner und Frauen (und alle nichtbinaeren Leute natuerlich auch) dazu bei, dass es den Menschen um sie herum gut geht … das ist wichtig fuer so eine Art grundlegenden Wohlstand. Aber es braucht nun mal einen Gauss, Goethe, Gates etc. pp. um neue Ideen zu entwickeln und eben _voran_ zu schreiten … was ueber die Menschheitsgeschichte gesehen als eine Rueckkopplung immer einen gehobenden grundlegenden Wohlstand zur Folge hatte … trotz aller furchtbaren Sachen die dabei auch geschehen … aber ach, ich will hier eigentlich gar nicht in eine derartige Richtung abschweifen.

Aber wenn man ueber die Intelligenz von Menschen redet … neee … das ist ja genau das Problem! Es gibt dazu nix handfestes! Und schon gar nicht in neuerer Zeit.
Aber ich greife vor. deswegen nochmal von vorne.

Meine zwei Einschuebe von neulich lieszen mich etwas unbefriedigt zurueck. Ich wollte klar machen, dass allgemeine Bildung extrem wichtig ist. Nicht nur fuer das Individuum oder besagten grundlegenden Wohlstand, sondern eben gesehen auf unsere gesamte Spezies und hunderte, ja tausende Jahre zurueck geschaut bzw. in die Zukunft projiziert.

Aber dann ist es eigentlich so, dass Bildung nur eine Art „Stellvertreter“ fuer ein viel unklareres Konzept ist. Dieses Konzept habe ich auch bereits angesprochen: Wohlstand.  Eine Erhøhung des Wohlstands, ob zeitlich und ørtlich lokal, oder global gesehen, geht immer mit einer Erhøhung des Bildungsniveaus einher. Aber auch das ist nur ein Stellvertreter fuer ein noch unklareres Konzept: Fortschritt.

Das Bildungsniveau ist (trotz aller Kritik) messbar auf dem individuellen, gesellschaftlichem, und globalen Level. Zensuren sagen zwar laengst nicht alles, sind aber i.A. doch korelliert mit spaeteren Lebenslaeufen. Auf „høheren“ Ebenen waeren konkrete Messgrøszen dann bspw. die Anzahl der Studienabschluesse, die Anzahl wissenschaftlicher Artikel oder (*schauder*) Patente pro Land und Jahrzehnt.
Das ist alles ganz und gar nicht „unkompliziert geradeaus“, aber man sieht zumindest statistisch robuste Korrelationen zwischen diesen Messgrøszen und der Anzahl der (weiterfuehrenden) Schulen und Schuljahre.

Wohlstand zu messen wird dann schon deutlich schwieriger. Das Bruttoinlandsprodukt ist gar nicht mal so schlecht. Dennoch muss man nur mal in die USA oder nach Sachsen schauen um zu sehen, wie wenig Wohlstand in groszen Gebieten und bei vielen Menschen vorhanden ist, trotz eines richtig guten Bruttoinlandsprodukts. Dennoch, auch fuer die allermeisten Menschen in diesen Bevølkerungsgruppen kommt der Strom zuverlaessig aus der Steckdose und das Wasser aus der Wand … verglichen mit all zu vielen nicht-„westlichen“ Laendern ist das ein immenser Wohlstand.

Und wo kommt der ganze Wohlstand heutzutage her? Na ganz klar, weil ein paar Individuen sich hingesetzt haben und erkannt haben, dass sich die Erde um die Sonne bewegt, dass ’ne Dampfmaschine benutzt werden kann um Minen zu entwaessern, dass man Stickstoff aus der Luft ziehen kann um damit Duenger herzustellen, dass man mittels abgestorbener Krankheitserreger Menschen immun machen kann gegen furchtbare Krankheiten, dass Halbleiter ganz toll sind um elektrisches Zeug zu schalten usw. usf. ueber viele Jahrtausende.

Aber wie zum Teufel soll man das messen? „Smart“phones sind definitiv Wohlstand, aber auch Fortschritt? Das Internet (was ist das eigentlich?) ist sicherlich Fortschritt, aber wie viele „Schritte“ hat es die Menschheit denn voran gebracht? Der Transistor und Strom (aus der Steckdose) sind definitiv als Fortschritt zu erkennen und diese zwei haben die Menschheit gewaltig viele Schritte voran gebracht. Aber was „messe“ ich denn da eigentlich und wie ist die Skala eingeteilt?

Ach du meine Nase!

Wir wollen Fortschritt, dass Konzept ist aber nicht klar definiert und kann somit nicht gemessen werden. Wir (als Menschheit) sind deswegen auf andere Konzepte ausgewichen und haben uns dann (als Menschheit) die Scheuklappen aufgesetzt und nur diese diskutiert.

Durch die Rueckkopplungsschleifen zwischen diesen drei Dingen wird es aber noch viel komplizierter.
James Clerk Maxwell konnte sich nur Gedanken um die Natur elektromagnetischer Wellen machen (Fortschritt), weil er die nøtige Bildung dafuer hatte. Und die nøtige Bildung hatte er nur, weil er nicht auf dem Feld Weizen anbauen mussten (Wohlstand). Er musste keinen Weizen anbauen, weil (nicht nur) die agrartechnischen Produktionsmethoden so viel besser waren als waehrend des rømischen Reiches.

Bildung zeugt Fortschritt zeugt Wohlstand zeugt Bildung … oder: Fortschritt zeugt Wohlstand zeugt Bildung zeugt Fortschritt … oder: Wohlstand zeugt Bildung zeugt Fortschritt zeugt Wohlstand.

Soweit ganz kurz zu den Sachen die diesem Artikel dieser kleinen Serie hier zugrunde liegen. Dieses ganze Themengebiet schwirrt mir schon seit vielen Jahren durch den Kopf. Meist im Zusammenhang mit, wohlwollend ausgedrueckt, eher konservativen Meinungen. In der direkten Form waeren solche Meinungen von der Art „Die Faulen sind selber Schuld, dass es denen so schlecht geht“. Aber sehr oft trifft man besagte Meinungen auch in der hinterhaeltigen Form an wie beispielsweise: „Wenn viele Leute die Homoehe nicht wollen, sollte man das dann gesetzlich verankern?“ … also im Sinne dessen, dass man Bevølkerungsgruppen die nicht sowieso schon am Reichtum teilhaben, die Teilnahme an besagtem Reichtum doch lieber nicht erlauben sollte … nur halt derart ausgedrueckt, dass es den Anschein hat, als ob der Rest der Bevølkerung das auch meint; deswegen „hinterhaeltig“.

Meine Antwort zu all diesen konservativen Meinungen ist: damit die Menschheit zu den Sternen gelangen kann, muss die Lebenssituation (a.k.a. Wohlstand) aller (!) Menschen verbessert werden. Dies nicht nur auf globalem, sondern auch auf lokalem, ja individuellem Niveau.
Der Grund ist, dass ich ueberzeugt bin, dass es immer noch viel zu viele Menschen wie Srinivasa Ramanujan gibt, nur dass auf diese niemand durch Zufall aufmerksam wird. Deswegen muessen sie ihr Potential benutzen um zu ueberleben anstatt den Warpantrieb zu erfinden. Etwas tangential, aber dies doch betreffend, frage ich mich bspw., wie viele „Verbrecherkønige“ eigentlich wirklich schlaue Menschen sind, die einfach nur ganz unten auf die Welt kamen und das der einzige realistische Ausweg war? … *seufz*.

Das ginge alles ganz einfach zu beweisen, wenn man zeigen kønnte, dass es urst viele wirklich schlaue Menschen in furchtbaren Lebensumstaenden gibt, und der Menschheit am besten geholfen waere, wenn man sich nicht auf zufaellige Entdeckungen durch Maezenin und Maezen verlaeszt. Wie soll man aber die Exzistenz von etwas beweisen, was es _offiziell_ gar nicht gibt?
Selbstverstaendlich gibt es diese intelligenten Menschen in furchtbaren Lebensumstaenden. Rein statistisch muss das schon so sein und die vielen Anekdoten tun ihr Uebriges um auf deren Vorhandensein zu schlieszen. Aber _offiziell_ gibt es diese Menschen erst, wenn sie bspw. in einer Studierendenstatistik auftreten oder wissenschaftiche Artikel verøffentlichen. Dies geschieht aber so oft nicht, weil die Lebensumstaende das nicht zulassen. Ergo, muessen wir die Lebensumstaende aller Menschen verbessern, weil wir begabte Individuen eben NICHT gezielt førdern kønnen, bevor diese „erkannt“ sind. Die Lebensumstaende aller werden aber nicht gehoben, weil das nicht als notwendig anerkannt ist fuer den Fortschritt (durchaus aus moralischen Gruenden aber mehr auch nicht). Somit bleiben begabte Menschen in besagten Lebensumstaenden  … da schlieszt sich der Kreis.

Und damit komme ich zum ganz konkreten Problem was ich im allerersten Satz dieses Artikels anriss. Damit das aber keine rein theoretische Diskussion wird, wollte ich es ueber einen ganz pragmatischen Ansatz versuchen: Fortschritt haengt von wirklich schlauen Leuten ab, von denen gibt es aber nicht so viele. Schlauheit messen wir nun ueber den „IQ“ (jaja, das Fass mache ich naechstes Mal ganz kurz auf … und dann ganz schnell wieder zu), und wenn wir den Durchschnitts-IQ aller Menschen erhøhen (bspw. durch Masznahmen welche die Lebensumstaende verbessern), dann fuehrt dies zu ueberproportional mehr wirklich schlauen Mensche und somit geht es schneller voran.

Dummerweise ist die Vermesung der Intelligenz ein schwieriges und  entzuendetes Thema in der Wissenschaft und Gesellschaft … aber ich møchte an dieser Stelle abbrechen, denn der Text hier ist schon wieder so lang. Ach verdammt … das sollte doch nur ein Artikel werden (siehe ganz oben) und nun wird’s doch wieder ’ne (kurze) Serie … nun ja, so ist das eben.

Eines der voll tollsten Weihnachtsgeschenke ever:

Foto nicht von mir aber mit Erlaubnis hier wiedergegeben.

Urst voll geil wa! Ein Original (!!!) der Philosophiæ Naturalis Principia Mathematica!
Es war aber die zweite, erweiterte Ausgabe. Habe ich sofort daran erkannt, weil darin auch Leibniz Darstellung der Infinitesimalrechnung aufgenommen war.

Freitags versuche ich immer ein Flash T-Shirt anzuziehen. Aus Prinzip und weil’s mein Lieblingssuperheld ist.
Dies im Speziellen hat nur aeuszerst periphaer mit dem Thema dieses Artikels zu tun: „Das dauert mir zu lange! Das muss doch schneller gehen!“ … Aber i.A. passt das schon … … … wobei „aueszerst peripher“ sinnlos ist, denn die Peripherie ist ja schon der aeuszere Rand einer Zone.

Ein ganz anderer Anfang: heute plaudere ich mal etwas aus dem Naehkaestchen und versuche mehrere Wochen des freudigen Programmierens und Problemløsens in nur diesen einen Beitrag zu packen, ohne all zu technisch zu werden.

Die neulich beschriebene Idee, das Kevin-Bacon-Problem in Vektoren zu fassen, ist streng genommen nicht nøtig um das Linknetzwerk zu durchschreiten. Es reicht vøllig, dass das alles in den Speicher passt und dann kann man (wie im verlinkten Artikel gesagt) mittels Fallunterscheidungen schon ’ne ganze Menge machen.

Nachdem ich die Titel zu Zahlen transformiert hatte, habe ich einen derartigen Algorithmus mal schnell implementiert um zu sehen, wie lange der denn braucht … und der brauchte so ca. 53 Jahre!

Wait! What!? Wenn ich mich richtig erinnere, dann hatte der Code noch nicht mal alle Analyseteile, welche noch mehr Zeit benøtigt haetten.
Dies war natuerlich zu viel und ich musste eine (mathematische) Løsung finden, welche dann hoffentlich nicht so viel Zeit braucht. Das ist das, was ich beim letzten Mal beschrieb.
Dieser „Vektorcode“, brauchte in Python 3.7.3 ca. vier Minuten um das Linknetzwerk einer Seite zu analysieren. Das war zwar besser, aber fuer alle ca. 6 Millionen Seiten waeren das immer noch 45 Jahre, die mein Rechner durchgehend haette laufen muessen. … Verdammt!

Da daemmerte mir, dass ich wohl nicht umhin komme, dass ganze in C zu schreiben.
Davor versuche ich mich immer zu druecken. Der Grund ist (wie an anderer Stelle bereits (indirekt) erwaehnt), dass ich mich da um grundlegende Sachen wie Speicherverwaltung selber kuemmern muss. Und wenn da was schief geht, dann bekomme ich das mitunter gar nicht mit, weil ich keine Ahnung von C habe.

Hinzu kam, dass die aeuszerste Ordnungsstruktur, das Lexikon (das „Dictionary“ oder die „Lokomotive“ (wie ich es an anderer Stelle nenne), welche die vielen „Waggons“ mit den ganzen Links „zieht“) in der Form gar nicht existiert in C. Zumindest nicht in der einfach zu verstehenden, einfach zu handhabenden und vielseitig anwendbaren Form wie in Python.
Und das ist ein riesiges Problem, denn auf jedem Linklevel, muss ich in besagtem Lexikon tausend-, millionen-, ja fast zweihundertmillionenmal nachschauen welcher Titel welche Links (die „Ausgaenge“ zum naechsten Linklevel) hat. Und das ganze dann noch mal ca. 6 Millionen Titel.
Deswegen muss so ein Lexikon effizient und gut in the gesamte Sprache integriert sein. Ich meine tatsaechlich die Programmiersprache an sich (und Dictionaries sind extrem gut in Python integriert), denn hierbei wird verdammt gute Speicherverwaltung benøtigt!

Zum Glueck hatte ich schonmal was von Hashtabellen gehørt. Hashtabellen sind sowas wie ein Lexikon — ein „Ausgangswert“ (hier die Titel) wird irgendwas zugeordnet. Dabei kann es aber zu sogenannten Kollisionen kommen. Das waren dann bei ein und demselben Ausgangswert mehrere Zuordnungen. Beim Lexikon nehme man das Wort „Wurzel“. Das kønnte die Wurzel einer Pflanze sein oder die Wurzel einer Zahl.
Hashtabellen løsen dieses Problem (muessen sie ja, denn ansonsten wuerden sie nicht benutzt werden) aber Kollisionsvermeidung fuehrt dazu, dass der Zugriff in Hashtabellen unter Umstaenden sehr langsam sein kann. Das ist ein riesiges Problem denn, wie bereits erwaehnt, muss ich urst oft in dieser Hashtabelle nachschlagen.
Vor allen Dingen ist die zeitraubende Kollisionsvermeidung ein unnøtiger Prozess in meinem Fall, weil ich nach der „Verzahlung“ eindeutige „Ausgangswerte“ habe und es niemals zu Kollisionen kommen kann.

Dazu kam, dass es auch solche Hashtabellen nicht „fertig aus der Tuete“ in C gibt und ich das selber programmieren musste.
Aber die 45 Jahre Laufzeit waren mir zu viel. Und deswegen machte ich mich auf, mir das Ganze mal anzuschauen. Zunaechst etwas zøgerlich, ja gar etwas aengstlich, aber dann immer enthusiastischer. Ich fand ein paar extrem gute Erklaerungen im Netz und die dortigen Løsungen schaffte ich fuer mein Problem zu modifizieren. Das war spannend!

Dann implementierte ich den beim letzten Mal vorgestellten Vektoralgorithmus und das ging ganz toll. Anstatt ca. 4 Minuten pro Titel brauchte ich nur noch 3.2 Sekunden (! … !!! … !!!einseinself) pro Titel … wait! WHAT?! … Anstatt 45 Jahre wuerde ich fuer alle ca. 6 Millionen Titel dann nur noch ca. 7 Monate brauchen!

JIPPIE!!!!! Damit wurde das Projekt ganz konkret durchfuehrbar.

Nun war besagte Zeit aber immer noch ohne die eigentliche Analyse.
Doch dann erinnerte ich mich, dass Computer heutzutage ja Mehrkernprozessoren haben, von denen meistens nur einer ausgelastet ist und der Rest Pause macht. Und die Macht dieser restlichen Kerne wollte ich auch nutzen. Das Ganze kønnte man auf deutsch „simultaner Mehrfadenbetrieb“ nennen, aber ich denke nicht, dass das irgendwer sagt. Deswegen benutze ich den englischen Begriff multithreading.
Wusste ich wie das zu programmieren ist? Die Antwort ist ein klares „Nein“. Aber das war super interessant und zunaechst etwas zøgerlich, ja gar etwas aengstlich, aber dann immer enthusiastischer machte ich mich daran die technische Seite des multithreading besser zu verstehen und zu implementieren.

Das hørt sich jetzt komplizierter an als es ist. Beim multithreading ist es eigentlich nur so, dass der Computer auf Kern #1 das Linknetzwerk von Titel 516 (als Beispiel) durchsucht, auf Kern #2 das von Titel 517, auf Kern #3 das von Titel 518 usw.
Dabei muss man im Wesentlichen darauf achten, dass bestimmte Ressourcen von allen „Threads“ benutzt werden. Beim Lesen ist das nicht so tragisch, da kann der Thread auf Kern #2 warten bis der Thread auf Kern #1 fertig ist. Beim Schreiben ist das aber von ganz erheblicher Bedeutung. Klar, wird da auch gewartet, aber der thread auf Kern #2 kønnte Information ueberschreiben, die der Thread auf Kern #1 (oder Kern #3 usw.) noch braucht.
Das wird oft dadurch geløst, dass man schaut welche Ressource gerade von welchem Thread „in Benutzung“ ist und die darf dann von keinem anderen Thread „angefasst“ werden. Das ist aber URST krass zeitraubend, weil dann ja wieder alle Prozessoren Pause machen bis die Ressource frei ist. Deswegen musste ich die Teile des Vektoralgorithmus welche von allen Threads benutzt werden auf andere weise „threadsicher“ machen. Die Løsung war, dass jeder Thread seine eigenen Vektoren bekommt und dann war es technisch nur noch eine kleine Herausforderung, dass die Zuteilung der Vektoren zu den richtigen Threads automatisch geschieht (weil das ja ca. 6 Millionen mal gemacht werden muss).

Lange Rede kurzer Sinn, nach der Hashtabelle implementierte ich dann das multithreading.
Nun ist es aber so, dass multithreading extra „Betriebskosten“ (diesmal nicht in Form von Speicher aber in Form von Prozessorzyklen und damit „Rechenzeit“) verursacht. Threadsicherheit ist der Teil der Kosten ueber den ich Kontrolle hatte. Das allermeiste geschieht intern und ich habe absolut keine Ahnung, was das alles ist.
Jedenfalls fuehrt das dazu, dass man die Zeit mit zwei Kernen nicht einfach nur halbieren kann. Aber bei 2 Kernen brauchte ich nur noch 2.8 Sekunden pro Titel. Und mit drei Kernen gar nur 2.2 Sekunden pro Titel. Die Benutzung von 4 Kernen bringt keine weitere Verbesserung, machte meinen Rechner aber urst traege. Das lag natuerlich daran, dass ich nur 4 Kerne habe und auf einem muss ja auch das Betriebssystem laufen.
Drei Theads, und ca. 5 Monate Rechenzeit, sollen es also sein.

Danach „stolperte“ ich ueber eine Kuriositaet, die ich mir nicht erklaeren kann. Dafuer muss ich aber etwas ausholen.

Die Werte der einzelnen Elemente in den Vektoren sind ja nur Null und Eins, nix anderes. Aber soweit habe ich den Algorithmus derart implementiert, dass ich diese als eben das — richtige Zahlen — ansehe, die auch den Wert 23517 annehmen kønnten. Damit folgen die mehrere Bytes Speicherbedarf „richtiger“ Zahlen. Weil es aber nur Nullen und Einsen sind, kønnte der Datentyp (und damit die „Betriebskosten“) dieser Werte auch anders sein.

Also spielte ich mal mit ein paar anderen Datentypen herum und es stellte sich dann heraus, dass ich mit der Verwendung des Datentyps char die Rechenzeit auf nur 1.5 Sekunden pro Titel reduzieren konnte. Das entspricht ein bisschen weniger als ca. 3 1/2 Monate fuer die komplette Wikipedia.
Der Nachteil von char ist, dass da dann halt nur kleine Zahlen rein passen, die nicht mehr als dieses eine Byte brauchen. Zum Glueck sind Null und Eins so klein, dass es kleiner nicht geht.

Superduper … doch dann ging mir auf, dass ich die Analyse der Linklevel ja noch gar nicht implementiert hatte. Das ging aber schnell reinzuhacken und die benøtigte Zeit erhøhte sich (bei der Verwendung von char und drei Threads) um nur 0.15 Sekunden pro Titel. Selbst bei fast 6 Millionen Titeln verlaengerte sich damit die erwartete Gesamtrechenzeit auf nur etwas mehr als ca. 3 1/2 Monate.

Lange Rede kurzer Sinn: nach einigen Wochen hatte ich es nicht nur geschafft die technische Løsung des Kevin-Bacon-Problems ganz konkret in Code zu fassen, sondern ich konnte durch gezielte „Tricks und Kniffe“ die Gesamtrechenzeit von urspruenglich ca. 50 Jahren auf nur 3 1/2 Monate reduzieren.

Da fuehlte ich mich ungefaehr so:

URST! KRASS! … WIE TOLL DOCH ICH BIN! … wa! … Es gibt nichts was ich nicht kann … ICH … BIN … GOTT!

Und deswegen wollte ich das hier mal (trotz der Laenge) wenigstens in der kuerzest møglichen Form mit so wenigen (konkret) technischen Ausfuehrungen wie møglich, hingeschrieben haben.

Dreieinhalbe Monate also. Sagen wir vier, vielleicht fuenf, denn es kønnte ja mittendrin was schief gehen und dann muss ich Teile nochmal machen.

… … … aber Moment … im Buero stehen doch zwei Rechner rum, die sonst nix zu tun haben … … …

… … … hmmmmmmmm … … …

… … … hmmmm hmmmm hmmmm … … …

… … … ca. 7 Wochen spaeter … … …

Die Ergebnisse sind hier!

Aber dazu mehr ab dem naechsten Mal.

Dies …

… ist der vorletzte Schuber in dieser Reihe. Und wenn ich ehrlich bin …

… dann freute ich mich beim Lesen darauf, dass ich bald fertig mit allem war. Die Gruende dafuer …

… legte ich mehr oder weniger detailliert in den letzten Beitraegen bereits dar. Und so kurz vor Schluss ist mir dann nochmal aufgefallen, …

… dass popkulturell sehr bekannte Figuren eigentlich eher spaerlich auftreten. Zwei Beispiele waren Pig-Pen (Schulz mochte nicht, dass diese Figur auf ihr Aeuszeres reduziert wurde und hat ihn deswegen sehr spaerlich eingesetzt) und Rerun (den ich sehr mag; wobei dieser ganz zum Schluss noch eine sehr wichtige Rolle spielen wird) und andere).

Das hat sicherlich damit zu tun, dass die TV-Serien (wo diese Charaktere mglw. grøszere Rollen haben) von viel mehr Menschen geschaut (und erinnert) wurden. Aber letztlich das ist ja dann eigentlich wieder genau das, was ich im allerersten Artikel dieser Reihe ansprach: der kulturelle Einfluss, den die Peanuts hatten und weiterhin haben … und weswegen ich alle Comicstrips haben wollte.

Die Drake-Gleichung …

… wird genommen um N,

[…] the number of civilizations in our galaxy with which communication might be possible […]

zu berechnen, als Produkt aus (alle Parameter sind anzusehen als Durchschnittswerte):
– der Rate der Sternenentstehung in unserer Galaxis, R_*;
– dem Anteil der Sterne die Planeten haben, f_p;
– der Anzahl der Planeten in der habitablen Zone, n_e („e“ fuer „Erde“);
– der Anteil der Planeten mit Leben, f_l,
– der Anteil der Planeten mit intelligentem Leben, f_i;
– der Anteil der Zivilisationen mit (der Faehigkeit zu bzw. Interesse an) interstellarer Kommunikation, f_c; und
– der Lebensdauer einer solchen Zivilisation, L.

Abhaengig von den Werten der Variablen kønnen da Werte von N bei rauskommen, die sich ueber hundert (!) Grøszenordnungen (!!!) unterscheiden. Das wird dann ab und zu auch kritisert, aber dafuer kann die Gleichung nix. Die ist nie dafuer gedacht gewesen um etwas exakt zu berechnen sondern zur Diskussion.
Einige der Werte kennen wir (mittlerweile) ziemlich genau (alle die mit Astronomie zu tun haben). Ueber andere wiederum wissen wir (fast) ueberhaupt nichts (alle die mit Biologie und Soziologie zu tun haben).

Im Laufe der Jahre hat die Mehrzahl der Leute, die sich darueber Gedanken gemacht haben, relativ hohe Werte fuer N ausgerechnet. Das bedeutet, dass es nach deren Berechnungen ziemlich viele Aliens um uns herum geben muesste. Und das ist das Fermi Paradoxon: wenn es so viele Aliens gibt, warum sehen wir von denen nix?

Deswegen wird spekuliert, was denn der grosze Filter sein kønnte, der diese Kommunikation von uns weg haelt?
Dadurch, dass wir (wie erwaehnt) mittlerweile ziemlich gut die astronomischen Parameter kennen, kønnten das nur noch die biologischen (also die Entstehung von Leben oder der „Aufstieg“ zur Intelligenz) oder soziologischen (Faehigkeit und Interesse an Kommunikation bzw. Lebensdauer einer Zivilisation) sein.

Sehr oft kann man das dazu zusammenfassen, dass das ja alles grundlegende physikalisch/biologische Konzepte sind, die ueberall im Universum gleich sind. Und selbst wenn wir da keine direkten Messwerte haben, kønnen wir ja von dem einen Messwert (die Erde/Menschheit) extrapolieren.
Auf dieser Basis argumentiert Whitmire, D. P. im International Journal of Astrobiology , 18 (2), 2019, pp. 183 – 188 in seinem Artikel mit dem Titel „Implication of our technological species being first and early„:

We argue […] that the Principle of Mediocrity implies that we are typical in technological age […].

Und das ist eine angebrachte, wohlerprobte und nicht zu beanstandende wissenschaftliche Herangehensweise — wir nehmen an, dass wir (und alles um uns herum) voll durchschnittlich sind. Mit Hilfe logischer und statistischer Argumente kommt Whitmire dann zum logischen Schluss:

[…] that the typical technological species has a short lifetime and that their extinction coincides with the extinction of their planetary biosphere.

Wie gesagt, das hier ist der Teil in dem alle sterben.

Eine Modifikation waere die sogenannte Dark Forest Theorie. Im Wesentlichen besagt diese, dass um uns herum keiner „Hallo“ ruft, weil das ja wer høren kønnte, der diese Wesen dann ausløscht, bzw. dass Logik diktiert, dass wenn wir einen Nachbarn høren der „Hallo“ sagt, wir den sofort umbringen muessen (was dann der Zirkel zum ersten Teil des Satzes ist), wenn wir als Zivilisation langfristig ueberleben wollen.
Dies ist natuerlich eine sehr anthropomorphe Sichtweise, aber Logik gilt doch ueberall im Universum.

Lange Rede kurzer Sinn: das Paradoxon løst sich auf, wenn man annimmt, dass alle intelligenten Zivilisationen schnell sterben und niemals die Sterne erreichen … Das ist schon ein bisschen deprimierend muss ich sagen.

Aber wie immer: (more) Science to the Rescue … beim naechsten Mal.

Nix Besonderes ist geschehen seit dem letzten Mal.

Auszderem habe ich den Eindruck, dass bei mir so ein bisschen Space Fatigue einsetzt. Mhmmmm … ich denke mal drueber nach, ob ich nicht erstmal eine nette, bewohnte Welt ansteuere und dort eine laengere Zeit Pause mache. Ich habe genuegend Credits auf meinem Konto und anstatt immerzu neue Sonnen zu sehen, kønnte ich mir ja mal ein paar Monate lang nur eine einzige Sonne auf den Bauch scheinen lassen.

Wieauchimmer, dafuer muesste ich erstmal wieder zurueck in bewohntes Gebiet. Bewohntes Gebiet ist aber recht weit entfernt z.Z.

Ebenso liegt dieses System …

… schon wieder ein Stueckchen hinter mir, in welchem ich 4 Wasserwelten vorfand. Nix super Spektakulaeres, aber durchaus schon etwas, was nicht so haeufig vorkommt.

Die Mensch-Computer-Schnittstellen werden immer besser. Lochkarten waren eine massive Verbesserung gegenueber dem Umstecken von Kabeln. Wobei natuerlich cool ist, dass der Beruf des Programmierers damals als inhaerent weiblich angesehen war. Interessant, wie sich die Zeiten aendern. Aber ich schweife ab.

Noch besser waren dann Tastaturen und heutzutage geben die User ihren Taschencomputern oft viel mehr Liebe als anderen Menschen, denn Erstere werden ja permanent gestreichelt, und Letztere nicht so oft.
In Star Trek reden alle nur noch mit Computern, so wunderschøn ausgedrueckt in dieser klassischen Szene, und dort bewegen wir uns mit schnellen Schritten hin (ab 1:18 geht die Demonstration los).

Aber trotz ausgeklugelter Technik wie Spracherkennung, so wird die Interaktion mit Computern doch im Allgemeinen als emotionslos dargestellt und angenommen. Zum Einen, weil Computer „Gefuehle nicht kønnen“, aber zum anderen auch, weil man die Maschinen nicht mit ambivalenten Dingen verwirren møchte … hier frage ich mich, warum wir das aber unseren Mitmenschen zutrauen?

Wieauchimmer, ganz gut zusammen fasst dieser Artikel ein paar der ueblichen (und wichtigen) Punkte bezueglich der „Computer kønnen kein Mitgefuehl (und werden das auch niemals kønnen)“.

Das ist ein extrem wichtiges Thema, denn so ziemlich alle (!) Berufe haengen daran. Nicht nur Lehrer und Krankenschwestern (und -brueder), sondern natuerlich auch die Polizei und auch der Chef auf dem Bau! Das ist immer und ueberall so praesent und krass wichtig, dass wir uns (als Individuen) ueber schlechte Chefs aufregen, bzw. (als Gesellschaft) diese fundamentale Faehigkeit zur Empathie einer ganz spezifischen Berufsgruppe versuchen abzuerziehen. Letzteres damit Soldaten ungestørt ihrer „Arbeit“ nachgehen kønnen; und in den allermeisten Faellen klappt das (zum Glueck) nicht.

Aber da wird natuerlich dran geforscht und es gibt gute Ideen (nur ein Beispiel) wie man an die Sache heran gehen kann. Solche Ideen gehen von dem aus, was wir ueber die Entwicklung kleiner Kinder wissen und legen dar, wie dieses „Geruest“ (welches von der Natur wohlerprobt ist) auf Maschinen uebertragen werden kann.

Tja … da geht sie hin, unsere Menschlichkeit … oder vielmehr erweitern wir „unsere“ Menschlichkeit und ich denke, dass dies ein richtiger Schritt in die Richtung ist, nicht zu Bueroklammern reduziert zu werden.

Aehnlich dem micromort vom letzten Mal beschreibt 1 microlife das Risiko inwieweit eine gegebene Aktivitaet eine halbe Stunde der Lebenserwartung „raubt“.

Das wurde natuerlich auch genauer untersucht … ach du meine Guete … zum Glueck wird mein langes zocken (minus 1 microlife pro 2 Stunden) teilweise dadurch kompensiert, dass ich heutzutage lebe und nicht vor 40 Jahren. Ebenso ermuntert mich das auch weiterhin mit dem Fahrrad zur Arbeit zu fahren, denn physische Aktivitaet hat einen positiven Wert. Wobei das wiederum auch total anders sein kønnte, denn zum Einen fahre ich an Straszen vorbei und bin der Luftverschmutzung ausgesetzt und zum Anderen hat Fahrradfahren einen Wert von 1 micromort pro 32 gefahrenen Kilometern … *seufz* … egal was ich mache, mich duenkt um’s sterben komm ich nicht drum herum.