Søren in Norwegen

Heute folgt ein langer und sehr technischer Beitrag. Das liegt daran, weil all dies hier den Warpantrieb der ganzen Problemløsungsmaschinerie beschreibt. Und weil’s eh schon so lang wird, verbrauche ich keine weiteren Worte fuer die Vorrede auf und frage gleich …

… wie muss ich mir eigentlich das Linknetzwerk der Wikipedia vorstellen?
Wenn man „Netzwerk“ hørt, dann denkt man mindestens an etwas Zweidimensionales und eine Form eines solchen zweidimensionalen Netzwerks kann man in den bekannten vereinfachten Beispielen sehen. Die Titel sind die Knotenpunkte und die Links dann die Pfade (zum naechsten Knotenpunkt).
Diese Vorstellung hat mir aber nicht geholfen eine Idee zu entwickeln, wie man technisch effizient dieses Netzwerk „abschreiten“ kønnte. Dann hatte ich das Sprachproblem aber „verzahlt“ und ab da formte sich (zunaechst unbewusst) in mir eine Idee.

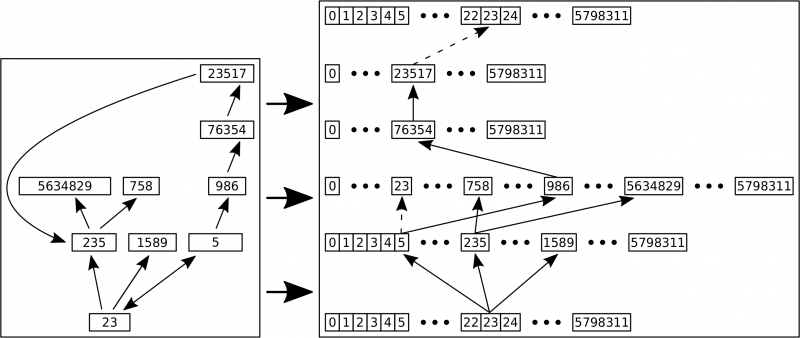
Aus den Titeln wurden fortlaufende (!) Nummern. Ich kann die also auf eine Zahlengerade setzen. Und von jedem Punkt komme ich zu ganz bestimmten anderen Punkten. Die Links sind also eine Abbildungsvorschrift — eine Funktion. Diese ist nicht bijektiv sondern nur surjektiv. Deswegen leuchtete mir zunaechst nicht ein, was die Zielmenge dieser Abbildung ist. Also malte ich mir das drei Tage lang immer und immer wieder in meinem Kopf aus:

Nur leider hing ich darin fest. Ich wusste nicht weiter, wie ich das technisch umsetzen soll. Also ich hatte schon ein paar Ideen, aber die schienen mir technisch nicht praktikabel. Der Grund war, dass ich mir ja auf jedem Linklevel merken muss, welche Knoten schon besucht waren, damit ich nicht in Schleifen gerate. Das ist an und fuer sich kein Problem, denn die kann ich einfach alle in einen „Waggon der schon besuchten Knoten“ stecken. Das Problem ist dann, dass ich fuer jede der ueber 161-Millionen Abbildungen haette schauen muessen, ob die in besagtem „Waggon“ ist (das sollen die gestrichelten Pfeile darstellen), oder nicht. Und egal wie das Ergebnis dieses Nachschauens war, ich muss dann immer noch eine Entscheidung treffen was danach zu tun sei. All das sind Rechenoperationen die viel Zeit kosten.

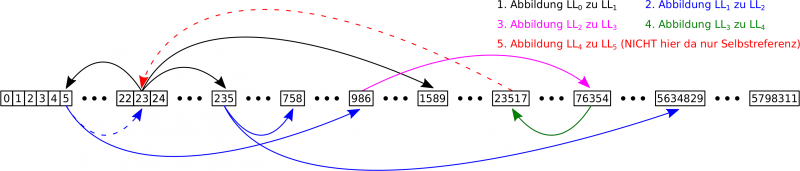
Nach drei Tagen daemmerte mir endlich die entscheidende Idee; zunaechst zøgernd, doch dann immer enthusiastischer: die Abbildungen bilden den Zahlenstrahl ja auf sich selber ab! Also buchstaeblich … bzw. wohl eher zahlstaeblich. Das Ganze sieht also viel eher so aus (LL = Linklevel):

Knoten die ich schonmal besucht hatte konnte ich nach dem ersten Besuch einfach „raussschmeiszen“ und wenn eine Abbildung dann ins Leere fuehrt macht das nix.

Und ziemlich schnell nach dieser entscheidenden Idee hatte ich gleich noch einen zwei Geistesblitze: diese Zahlengerade ist ja ein Vektor! … mit 5,798,312 Dimensionen (die Zahlengerade zaehlt nur nur bis 5,798,311, weil ich bei der Null anfange zu zaehlen). Und jede Abbildung zeigt auf genau einen Punkt in diesem vieldimensionalen Raum!

Aber wenn ich das als einen Vektor sehen kann, dann kann ich das Problem doch mit den simpelsten Methoden der linearen Algebra angehen! Und lineare Algebra ist doch genau das, wofuer Computer gebaut wurden. Das bedeutet, dass ich anstatt umstaendlicher und Prozessorzeit verbrauchender „nachschauen und mittels verzweigter Anweisungen Entscheidungen treffen“-Operationen einfach nur Vektoren miteinander addieren und multiplizieren kann.

Und hier kommt jetzt die Genialitaet der beim letzten Mal besprochenen Abbildung der Wørter auf (ganze) Zahlen zum Tragen … und ein weiterer Geistesblitz: der Wert einer Zahl, entspricht der Position AUF dem Zahlenstrahl. Ist ja voll banal die Erkenntnis, aber in „Vektorform“ bedeutet dies: jeder Titel (als Zahlenwert) entspricht einem eindeutigen (!) Einheitsvektor in diesem multidimensionalen Vektorraum! Ein Einheitsvektor hat nun aber die Laenge 1. Das bedeutet, dass der Zahlenwert des Titels die Position in diesem spezifischen Einheitsvektor bestimmt, die NICHT Null wird, sondern Eins. Geil wa!

OK, ich gebe zu, das ist alles etwas abstrakt. Deswegen gehen wir mal gemeinsam der Reihe nach durch die technische Umsetzung.

Zunaechst einmal habe ich ja mein Lexikon in dem steht welcher Titel welche Links hat. Das behalten wir im Hinterkopf fuer wenn wir das brauchen. Andernfalls steht das nur passiv im Hintergrund rum, ich schlage spaeter darin nur nach wo die Links zu jedem Titel hinfuehren.

Das Folgende machen wir dann fuer jeden Titel.

Zunaechst initialisieren wir drei Vektoren mit 5,798,312 Dimensionen.
Der eine Vektor stellt alle Titel dar, die wir schon „besucht“ haben. Da wir im Moment noch keinen Titel besucht haben, stehen da ueberall Einsen. Nach dem Besuch schmeiszen wir die Eins an der Stelle des besuchten Titels raus (und zurueck bleibt eine Null). Das wird wichtig fuer spaeter. Diesen Vektor nenne ich < Verbleibend >.
Der zweite Vektor repraesentiert alle Titel die sich auf dem gerade unter Untersuchung befindlichen Linklevel befinden und NICHT bereits vorher besucht wurden. Die Elemente dieses Vektors sind alle Null, AUSZER wenn ich auf dem gegebenen Linklevel zum ersten Mal auf diesen Titel treffe. Dann wird wird der Wert des Vektors an der Stelle die dem Zahlenwert des Titels entspricht Eins. Ich nenne diesen Vektor < Jetzt >.
Den dritte Vektor nenne ich < Abbildung >. Dieser wird ebenso mit Nullen initialisiert und repraesentiert spaeter die „Ausgaenge“ von einem Linklevel zum naechsten.

Da wir uns ganz am Anfang befinden ist < Jetzt > natuerlich komplett „leer“ (also besteht nur aus Nullen). Dito, ist < Verbleibend > total „voll“ (besteht also nur aus Einsen). Fuer beide gilt eine Ausnahme, naemlich an der Position des einen Titels, dessen Linknetzwerk wir erforschen møchten. Im obigen Beispiel waere es dann Position 23 an der eine Eins in < Jetzt > bzw. eine Null in < Verbleibend > steht.
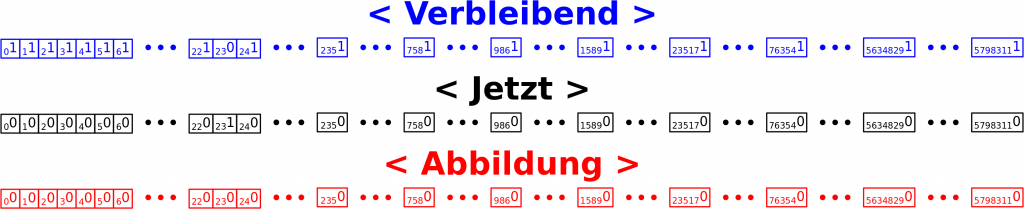
Fuer das Beispiel sehen die drei Vektoren als Zeilenvektor nach der Initialisierung so aus:

Die Indizes links unten an jeder Null oder Eins repreaesentieren die Positionen (oder Dimensionen im Sinne von x, y, z …) im Vektor. Man beachte, dass ich bei Null anfange zu zaehlen. An die richtige Position gelange ich einfach durch den Zahlenwert der betreffenden Titel. Man beachte ebenso, dass fuer < Verbleibend > und < Jetzt > der Wert an Stelle 23 anders ist als fuer alle anderen Positionen in diesen beiden Vektoren. Dies gilt nicht fuer < Abbildung >, denn wir haben ja gerade erst alles initialisiert und noch gar nicht geschaut, wo die 23 hin fuehrt.

Deswegen schauen wir im naechsten Schritt im Lexikon fuer _alle_ Titel die eine Eins in < Jetzt > haben (die also neu besuchte Titel auf diesem Linklevel sind) nach, wohin die fuehren. Die Zahlwerte dieser Links bestimmen auf welchen Positionen darauf im Vektor < Abbildung > eine Eins zu setzen ist. Im Beispiel muessen wir das erstmal nur fuer die 23 tun:

Danach finden drei der vier Auswertungen statt. Zum Ersten evaluiere ich, wie oft auf dem gegebenen Linklevel der urspruengliche Titel zitiert wird (Selbstreferenz). Im gezeigten Beispiel ist das nicht der Fall aber im Allgemeinen passiert das durchaus.
Zum Zweiten schaue ich pro Linklevel, welche Seiten zitiert werden, aber nur OB und NICHT wie oft die zitiert werden. In der Untersuchung des Linknetzwerkes fuer nur einen Titel, dann ist dieser Wert pro Linklevel fuer alle anderen Titel entweder einmal oder keinmal. Aber ich schaue mir das ja fuer alle fast 6 Millionen Titel an. Ich mache das auf diese Weise, weil mich interessiert, ob es Seiten gibt die prinzipiell eher bei høheren Linkleveln zitiert werden, verglichen mit „normalen“ Seiten. Deswegen kann ich hier auch nur „ob“ und nicht „wie oft“ zaehlen (im Unterschied zur Selbstreferenz), denn dann wuerden „populaere“ Seiten durch die schiere Anzahl der Zitate die diese bekommen das Signal verfaelschen.
Rein praktisch muss ich dafuer nur < Abbildung > auswerten und mir fuer das gegebene Linklevel merken, an welchen Positionen dieser Vektor nicht Null ist. Cool wa! So einfach ist das.
Als Drittes werte ich die Anzahl der totalen „Ausgaenge“ von diesem Linklevel zum naechsten aus. Das entspricht einfach nur der Summennorm (oder Laenge) des Vektors < Abbildung >.

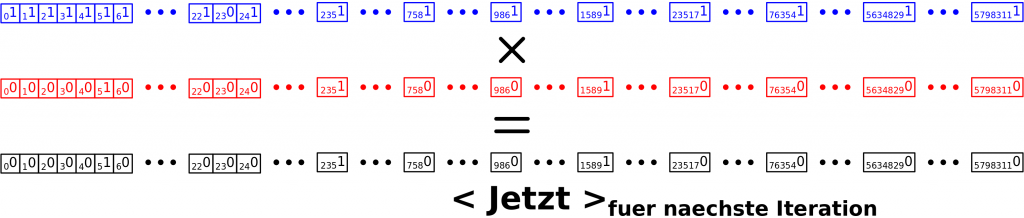
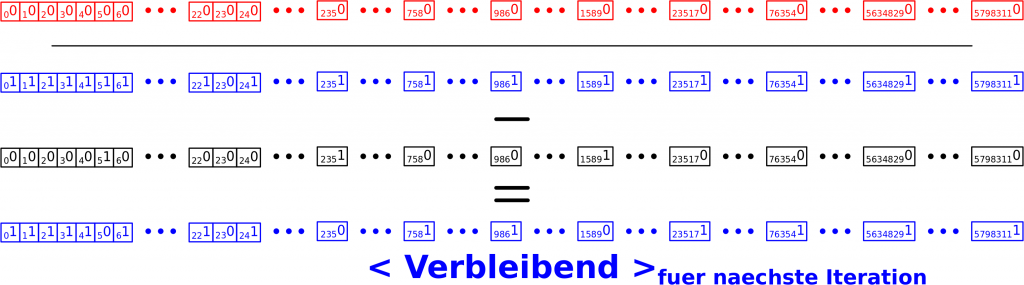
Nun muss ich die naechste Iteration vorbereiten. Zunaechst muss < Jetzt > in der naechsten Iteration an den Positionen eine Eins haben zu denen ein „Ausgang“ fuehrt. Unter der Einschraenkung, dass diese Positionen nicht auf einem frueheren Linklevel bereits besucht wurden! Das kann ich einfach durch eine elementweise (!) Multiplikation von < Verbleibend > mit < Abbildung > erreichen:

Das hier ist so geil! Man nehme an, dass < Abbildung > (also die „Ausgaenge“ vom jetzigen Linklevel zum naechsten) an einer bestimmten Stelle einen Wert von Eins hat (einfach weil das halt ein Link ist der auf diesem Linklevel auftaucht und dorthin will). Man nehme weiter an, dass ich den Titel der dieser Position entspricht aber schon besucht habe. In dem Fall hat < Verbleibend > an der selben Position einen Wert von Null. Somit wird das Produkt der Elemente der beiden Vektoren an dieser Position fuer den < Jetzt > Vektor der naechsten Iteration auch Null. Und das ist wichtig, denn ein Element in < Jetzt > soll ja nur dann Eins sein, wenn ich da noch nicht war, damit ich nicht in unendliche Schleifen gerate. Das wird klarer an Position 23, wenn ich weiter unten die Vektoren fuer die zweite Iteration voll ausschreibe.

An dieser Stelle nehme ich dann die letzte Auswertung vor. Die Laenge des neuen (!) < Jetzt > Vektors, ergibt die Anzahl der neuen, noch nicht besuchten „Ausgaenge“ auf diesem Linklevel, mit der gegebenen Startseite. Das møchte ich zusaetzlich zur obigen Anzahl der totalen „Ausgaenge“ wissen, denn nur die neuen zu besuchenden Seiten verlaengern die Kette von Kevin Bacon zu anderen Seiten der Wikipedia.
Das hier muss ich uebrigens sowieso auswerten, denn dies ist die Abbruchbedingung fuer die aeuszerste Schleife. Das bedeutet, dass wenn die Laenge des neuen < Jetzt > Vektors null wird (wenn es also keine „Ausgaenge“ zu noch nicht besuchten Seiten gibt), dann habe ich das komplette Linknetzwerk fuer die gegebene Startseite besucht. In dem Fall kann das ganze Prozedere natuerlich fuer den naechsten Titel von vorne beginnen.

Aber dies ist meistens erst bei høheren Linkleveln der Fall und deswegen møchte ich nun erstmal das naechste Linklevel untersuchen. Dafuer muss ich noch zwei letzte Sachen vorbereiten. Zum Einen muss < Abbildung > wieder zu null initialisiert werden (damit da in der naechsten Iteration wieder nur die neuen „Ausgaenge“ drin stehen). Zum Zweiten muss der neue < Verbleibend > Vektor berechent werden; ich habe ja jetzt mehr Seiten als zu Beginn der Iteration gesehen. Das ist ganz einfach, denn hier muss ich nur den (neuen) < Jetzt > Vektor vom bisherigen (alten) < Verbleibend > Vektor subtrahieren.

Und so einfach, meine lieben Leserinnen und Leser, ist die Løsung des Kevin-Bacon-Problems! Das ist ja wohl mal voll geil, wa! Deswegen schrieb ich ganz oben auch „Warpantrieb“, denn dadurch, dass ich hier nur Nullen und Einsen lesen, schreiben, multiplizieren und subtrahieren muss kann das ganze urst schnell berechnet werden … naja … „urst schnell“ ist relativ und ich komme darauf an anderer Stelle zurueck.

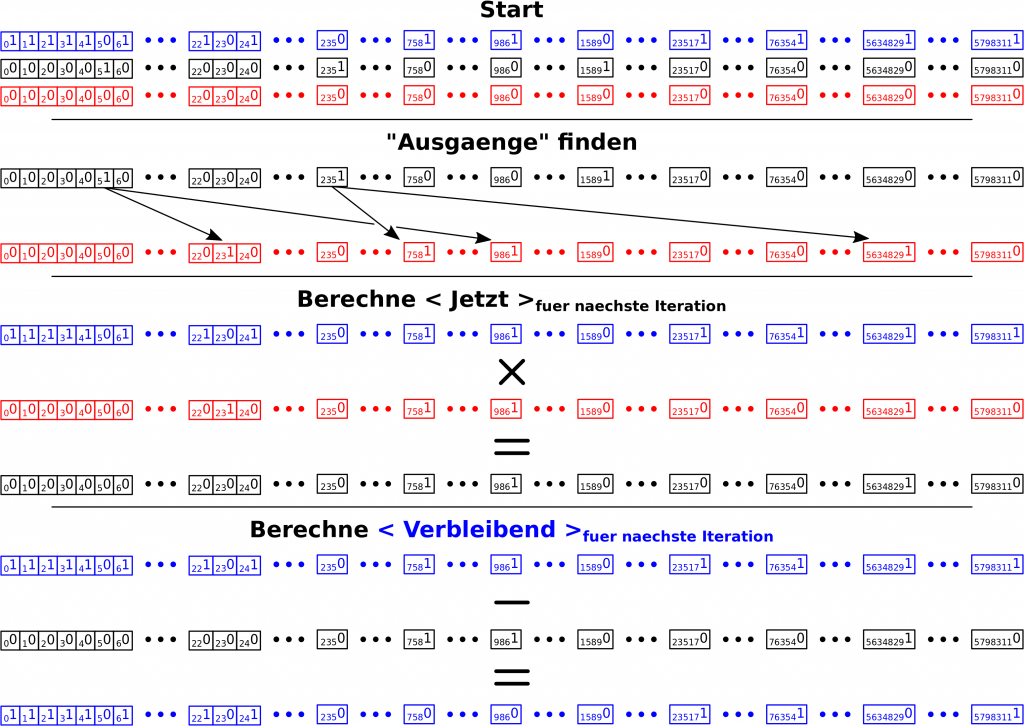
Hier nun in visueller Form die selben Schritte fuer Linklevel 2 des Beispiels:

In dieser zweiten Iteration wird an drei Stellen sichtbarer, warum ich das alles so geil finde … und damit auch mich so toll finde, weil ich da von alleine drauf gekommen bin.
Im Schritt „Ausgaenge finden“ wird < Abbildung > an Position 23 natuerlich zu 1 gesetzt (das ist noch nicht das Fetzige). 5 will da hin, selbst wenn ich da schon war. Wenn ich dann aber < Jetzt >_{fuer naechste Iteration} berechne wird das Element an Position 23 (wie oben bereits erwaehnt) durch die Multiplikation mit < Verbleibend > zu Null. DAS ist das erste Fetzige, denn diese Multiplikation ist oben besagte Kontrolle, dass ich nur bei Titeln weiter gehe, die ich noch nicht besucht hatte. Das ganze aber ohne Prozessorzeit verbrauchende Fallunterscheidungen.
Bei der selben Berechnung sieht man auch, dass die „Ausgaenge“ nicht einzeln „durchschritten“ werden (so wie wenn ein Mensch mit den Augen den Pfeilen folgt), sondern alle gleichzeitig! Das ist das zweite Fetzige.
Das dritte Fetzige ist dann letztlich, wenn < Verbleibend >_{fuer naechste Iteration} berechnet wird. Dort sieht man, wie die Laenge dieses Vektors von Linklevel zu Linklevel immer kleiner wird, weil immer mehr Einsen zu Nullen werden. Das soll ja auch so sein, denn ich habe ja immer mehr und mehr Wikipediaseiten gesehen von Linklevel zu Linklevel.

Und das ist alles so fetzig, weil die ganzen die Problemløsung bzgl. der Uebersicht ueber wichtige Aspekte zu behalten, einfach so aus der „Mathematisierung und Verzahlung“ mit „heraus fallen“.
Haette ich hier uebrigens nur den Code hinkopiert, so waere dieser Artikel deutlich kuerzer, aber mglw. auch deutlich weniger verstaendlich, gewesen. Denn der Warpkern der Problemløsungsmaschinerie sind nur ’n paar Zeilen Code.

Fuer die tatsaechliche Implementation brauchte ich mehrere Wochen. Ich musste das naemlich letztlich in C programmieren (womit ich mich fast gar nicht auskenne) UND ich wollte das parallelisieren, dass also die Linknetzwerke mehrerer Titel gleichzeitig durchschritten werden. Diese Herausforderung war aber sooooooo herrlich und das zustande bringen der (technisch, praktikablen) Løsung soooooo befriedigend.
Damit meldet sich mein innerer Zefram Cochrane fuer heute ab.