Endlich kann ich ueber diesen Geniestreich reden … aber ich greife vor.
Beim vorletzten Mal „mathematisierte“ ich das Kevin-Bacon-Problem. Das war prinzipiell løsbar, aber ich stellte beim letzten Mal fest, dass es aufgrund von Speicherplatzmangel technisch in der gegebenen Form praktisch nicht løsbar war.
Ich redete beim letzten Mal viel ueber die „Betriebskosten“ (in Form von Speicher) die Datenobjekte haben. Dabei konzentrierte ich mich auf Wortobjekte. Fuer jedes Wort habe ich „Betriebskosten“ von 49 Bytes plus der Speicherbedarf der „Nutzlast“ von 1 Byte pro Buchstabe. Die „Nutzlast“ ist von der Laenge des Wortes abhaengig.
Ich erwaehnte auch, dass eine Zahl keine Laenge hat. Cool ist nun, dass der Gesamtspeicherbedarf („Betriebskosten“ + „Nutzlast“) einer ganzen Zahl auf meinem Rechner unter Python 3.7.3 deutlich kleiner ist als fuer Wørter; naemlich nur 28 Bytes. Und das ist unabhaengig davon, wie grosz die Zahl wird! … Naja, es gibt natuerlich Ausnahmen. Die Null braucht nur 24 Bytes und ganz grosze Zahlen (genauer gesagt ab 1,073,741,824) brauchen dann schon 32 Byte und irgendwann werden die Zahlen so grosz, dass die 36 Byte brauchen usw. Aber das ist hier nicht von Interesse, da ich nicht in diese groszen Bereiche komme mit dem gegebenen Problem.
Und hier kommt jetzt die geniale Idee: Ich bildete jeden Titel auf eine nicht negative ganze Zahl (inklusive der Null) ab. Wenn ein Titel von einem anderen Titel zitiert wird, dann erstatte ich diesen mit der gegebenen Zahl. Die Reihenfolge spielt dabei ueberhaupt keine Rolle. Diese Abbildung ist bijektiv und die Abbildungsvorschrift (einfach eine lange Tabelle welcher Titel welcher Zahl zugeordnet ist) merke ich mir natuerlich, falls ich spaeter eine spezfische Linkkette nachverfolgen will.
Durch die Abbildung auf nicht negative ganze Zahlen verringerte sich der Speicherbedarf meiner 5,798,312 Titel und 165,913,569 Links von ehedem 11 GB auf 4,807,932,668 als ca. 4.8 GB … Huzzah!
Damit habe ich das Kevin-Bacon-Problem nicht nur mathematisiert, sondern auch „verzahlt“. Das coole ist, dass sich dabei der Informationsinhalt, bzgl. der Informationen, an denen ich interessiert war (!), nicht veraenderte. Cool wa!
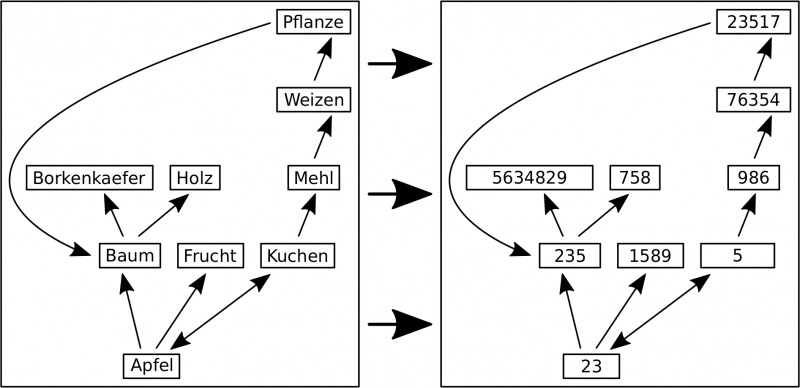
Zur Veranschaulichung hier das dritte Beispiel vom vorletzten Mal in der neuen Darstellung:
Mit dem Bild erkennt man besser, dass sich der untersuchte Informationsinhalt nicht aendert. Ob Apfel jetzt auf Kuchen zeigt oder 23 auf 5 tut nix zur Sache, solange im gesamten Netzwerk 23 immer mit Apfel und 5 immer mit Kuchen assoziiert ist.
Zum Problem der „Betriebskosten“ der Wortobjekte kamen beim letzen Mal die Betriebskosten der „Waggons“ (oder Ueberstrukturen) in denen diese aufbewahrt wurden. Ein Problem wurde es deshalb, weil jeder Titel einen solchen „Waggon“ hat. Ganz spezifisch waren diese „Waggons“ sogenannte Sets und deren „Betriebskosten“ waren abhaengig von der Anzahl der darin enthaltenen Elemente.
Das Gute ist nun, dass es noch andere Arten von „Waggons“ gibt. Fuer den Verwendungszweck hier ist nur wichtig, dass diese die „Aufbewahrungsbox“ aller zu einem Titel gehørenden Links sind, damit nix durcheinander kommt. Dafuer brauche ich kein Set, wie beim letzten Mal erwaehnt, sondern es reicht ein sogenannten Tupel.
Waehrend man mit Sets urst viel machen kann (bspw. Elemente heraus nehmen oder dazu packen, oder Mengenoperationen mit anderen Sets ausfuehren) kann man mit Tuples (fast) nix machen. Das ist ein unveraenderbarer „Kasten“ fuer meine Links (die ja nun Zahlen sind). Und weil man damit so wenig machen kann, betragen die „Betriebskosten“ eines leeren Tuples nur 56 Bytes und die steigen linear an (diesmal wirklich) mit 8 Byte pro neuem Element.
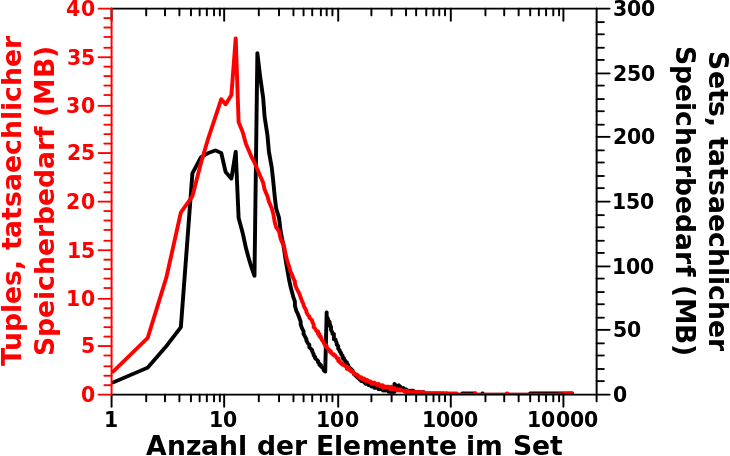
Wie beim letzten Mal brauche ich nun das Produkt aus der Verteilung der Links pro Titel und dem tatsaechlichen Speicherbedarf der Tuples. Zum Vergleich habe ich in dieses Diagramm das Resultat dieser Rechnung und der gleichen Rechnung vom letzten Mal dargestellt.
So ein Mist, da aendert sich ja nicht viel … ach nee! Die Skala der linken Ordinate ist eine ganze Grøszenordnung (!) kleiner als die Skala der rechten Ordinate … voll krass!
Der Gesamtspeicherbedarf betraegt damit fuer alle „Tuple-Waggons“ keine 11 GB wie bei den Sets, sondern nur 1,605,627,528 Bytes also ca. 1.6 GB.
Da kommen dann noch die ca. 300 MB fuer die oberste Struktur hinzu, welches alle „Waggons“ den richtigen Titeln zuordnen (die „Lokomtive“ vom letzten Mal bzw. das „Dictionary“). Insgesamt benøtige ich mit diesen Modifikationen dann nur noch 6,7 GB.
JIPPIE! So viel Speicher habe ich und deswegen soll das fuer heute reichen. So viel sei nur noch gesagt: hier hingeschrieben hørt sich der Schritt der Abbildung der Titel auf ganze Zahlen voll logisch an. Deswegen war dieser Geniestreich als solcher auch zunaechst unbemerkt. Ich wollte ja erstmal nur das Speicherplatzproblem løsen. Aber letztlich erlaubte mir erst dieser Schritt die (effiziente!) technische Implementierung der Løsung des eigentlichen Problems. Dazu Bedarf es allerdings noch ein paar weiterer (Achtung: Spoiler) „Transformationen“.
Leave a Reply