Søren in Norwegen

Beim letzten Mal beschrieb ich die Umwandlung des urspruenglichen Sprachproblems in ein mathematisches Problem. Damit kann man prinzipiell so wie’s ist (von Apfel zu Kuchen zu Mehl usw.) an die Sache heran gehen.
Wir sprechen hier aber von fast 6 Millionen Knoten (Wikipediatiteln) und mehr als 181-Millionen Verbindungen dazwischen in diesem Netzwerk. Und fuer jeden Knoten muss ich die Gesamtheit der Verbindungen „abschreiten“. Dabei lief ich in ein albekanntes Problem: nicht genug Speicher! Aber der Reihe nach.

Vor ein paar Monden hørte ich mit der Saeuberung der Rohdaten auf und es blieben noch …

[…] 5,798,312 Wikipediaseiten auf denen insgesamt 165,913,569 Links erscheinen […]

… zurueck.

Ich schrieb auch, dass der Speicherbedarf dieser Daten von ehemals ueber 70 GB (die gesamte Wikipedia) auf 4.1 GB verringert wurde. Ich hatte das auf 61 Dateien verteilt und die bin ich fuer die bereits vorgestellten Untersuchungen immer der Reihe nach durchgegangen (denn da hat mich ja das Netzwerk an sich nicht interessiert).
Das Komische war nun, dass das eigentlich alles in den Speicher meines Laptops passen sollte … aber irgendwie kam dieser nicht zurecht, wenn ich versuchte mehr als 10 dieser Dateien gleichzeitig zu laden.

Merkwuerdig … wie sieht das denn eigentlich im Speicher aus?
Nunja, erstmal dachte ich ganz einfach, dass die Titel der Seiten Buchstabenketten (allgemeiner: Zeichenketten) mit einer bestimmten Laenge sind. Dito bzgl. der Links „hinter“ jedem Titel.
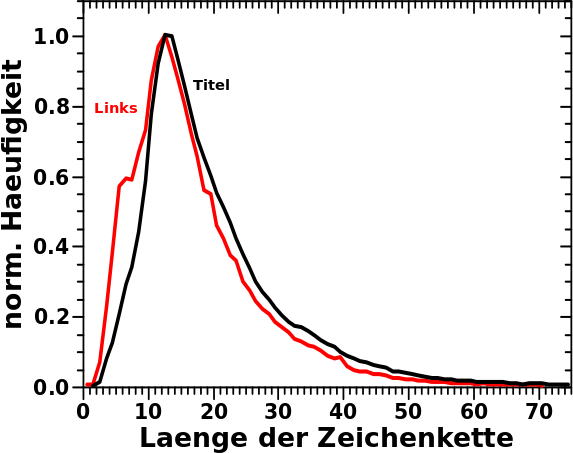
Im Wesentlichen braucht ein Buchstabe im Speicher 1 Byte … jaja, Sonderzeichen brauchen mglw. mehr, aber ich sollte davon nicht soooo viele haben … Der Speicherbedarf der Titel sollte also das Integral ueber die hier gezeigte Verteilung sein: 117,194,976 Bytes also ca. 117 MB.
Die Verteilung der Laengen der Links ist sehr aehnlich:

In den nicht normierten Daten ist die Amplitude der Verteilung der Links natuerlich viel grøszer und diese muss natuerlich fuer das Integral genommen werden.
Nebenbemerkung: das kleine „Uebergewicht“ bzw. „Untergewicht“ links bzw. rechts vom Maximum ist sicherlich dadurch zu erklaeren, dass „prominente“ (also oft zitierte) Seiten einen kurzen und knackigen Titel haben — siehe hier. Der Unterschied ist zwar zu sehen, aber nicht so massiv (oder unerwartet), sodass ich mich da nicht weiter fuer interessiere. Insb. auch deswegen nicht, weil die gegebene Erklaerung (mit den Beispielen der meistzitierten Seiten) durchaus plausibel klingt.

Fuer den Speicherbedarf aller in den Links enthaltenen Zeichen errechnete ich nun: 2,898,076,329 also ca. 2.9 GB.

Na sowas! Meine simplen Ueberlegungen løsen die Merkwuerdigkeit nicht auf!
Des Raetsels Løsung ist zweigeteilt und ich gebe zu, dass das ueber das Anfaengerprogrammiererniveau hinaus geht (wenn auch nicht sehr weit). Aber dafuer muss ich etwas ausholen. Das wiederum handelt im vorbeigehen auch gleich etwas ab, was beim naechsten Mal total hilft :) .

Nehmen wir die Zeichenkette „gerader Strich mit kurzer Kappe, zwei mal zwei nach links offene Halbkreise, schraeger Strich mit Vordach“ — oder in kurz 1337.
Ich nehme 1337 mit Absicht. Zum Einen ist es natuerlich die Zahl Eintausenddreihundertsiebenundreiszig. Dann es aber auch das bekannteste Beispiel fuer Leetspeak und wird eben auch direkt als „LEET“ — also ein Wort — interpretiert.
Ein und die selbe (!) Zeichenkette hat also zwei unterschiedliche Bedeutungen. So wir denn von diesen Unterschieden wissen, so ist das fuer uns Menschen i.A. kein Problem 1337 kontextabhaengig richtig zu interpretieren. Wenn ich also sage packe bei 1337 nochmal 1337 ran, so ist das eine Addition im Falle der Zahl und das Ergebnis wird 2274 bzw. wird is im Falle des Wortes 13371337 (also LEETLEET).

Damit bin ich bei einem weiteren wichtigen Aspekt: Operationen.
Abhaengig von der Bedeutung die die Zeichenkette hat, kann man damit unterschiedliche Operationen ausfuehren oder gleiche Operationen, die aber unterschiedliche Ergebnisse haben. Oben erwaehnte ich die Addition. Eine andere Operation waere „Sag mir mal die Laenge von dem was ich gerade vor mir habe“.
Bei LEET entspricht die Laenge natuerlich der Anzahl der Zeichen und ist somit vier. Aber selbst wenn eine Zahl viele Zahlzeichen enthaelt, so ist die Laenge einer Zahl doch immer eins! Das ist besser zu verstehen, wenn man rømische Zahlsymbole nimmt, denn da sind 10, 50, 100, 500 und 1000 nur ein Symbol. Noch cooler ist das cistercianische Zahlsystem, welches bis 9999 immer nur ein Symbol braucht.

Das alles weisz man „automatisch“ als Mensch, aber dem Computer muss man zu jeder Zeichenkette sagen, was die jetzt eigentlich fuer eine Bedeutung hat, damit die richtigen Operationen drauf ausgefuehrt werden. Und hat eine Zeichenkette erstmal eine Bedeutung, so aendert die sich niemals … … … jaja, ich weisz, dass es da Spezialfaelle gibt, die Ausnahmen zu dieser Aussage sind … aber mir geht’s hier darum, dass man einem Computer explizit und jedes Mal sagen muss, womit dieser eigentlich gerade arbeitet.
Das ganze geht natuerlich noch viel tiefer direkt rein in die Innereien des Computers. Denn eine Zahl ist im Speicher ganz anders dargestellt als ein Wort.

Worauf ich hinaus will ist das Folgende. Jedes Objekt im Program (also meine Zeichenketten) hat „Betriebskosten“ in Form von Speicherplatzbedarf wo eben die Bedeutung des besagten Objektes abgelegt ist. Diese „Betriebskosten“ beinhalten das was ich oben sagte, damit der Computer weisz, wie mit besagten Objekten umzugehen ist. Interessiert bin ich aber nur an der „Ladung“ eines Objektes; also der Zahl oder dem Wort an sich. Diese „Ladung“ kommt zu den „Betriebskosten“ hinzu.

Um die „Betriebskosten“ kommt man niemals drumherum und es gibt nun zwei Møglichkeiten, wie man das handhaben kann. Zentral oder dezentral.
Zentral bedeutet, dass man eine gewisse Menge Speicherplatz reserviert und ranschreibt welche Bedeutung alle Objekte die sich darin befinden haben. Dann muss man das nur einmal sagen und die „Betriebskosten“ fallen nur einmal an.
Dezentral bedeutet, dass man das an jedes einzelne Objekt ranschreibt. Dann fallen die „Betriebskosten“ fuer jedes Objekt an. Warum sollte man das machen? Naja, dafuer gibt es technische Gruende, und mindestens einen eher philosophischen Grund: um dem Menschen der das Programm schreibt die Arbeit zu erleichtern. Denn das ist genau das was Python macht. Speicher- und Objektmanagement sind Dinge, die man in anderen Programmiersprachen explizit machen muss. Ich finde das durchaus interessant, aber ich gebe zu, dass es vom eigentlichen Programmieren (sich logische Strukturen ueberlegen, die ein gewisses Problem løsen) abhaelt, wenn man das „Inventar“ immer „sortieren und sauber halten“ muss.

Und das ist das was ueber das Anfaengerprogrammiererniveau zumindest unter Python hinausgeht. „Anfaengerprogrammiererniveau“ deswegen, weil Python heutzutage nunmal die Sprache ist, in der mglw. die allermeisten Leute anfangen zu programmieren. Und die fangen damit an, eben weil da solche Sachen im Hintergrund passieren  und vom Menschen der den Code schreibt weg gehalten werden.
Es ist aber natuerlich auch Grund, warum Python nicht fuer die Programmierung wirklich groszer Programme (wie bspw. Betriebssysteme) benutzt wird. Hat halt alles seine Vor- und Nachteile.

Soweit dazu. Den Speicherbedarf der „Ladung“ habe ich oben berechnet. Aber wie grosz sind denn nun die „Betriebskosten“ pro Zeichenkette? Nun ja, das ist kompliziert und nicht nur von der Architektur des Rechners und Betriebssystems, sondern auch der benutzten Inkarnation der Programmiersprache abhaengig. Unter Python 3.7.3 auf meinem Rechner belaufen sich besagte „Betriebskosten“ von Zeichenketten auf 49 Byte pro Objekt. (Unter Python 2.7.16 sind es uebrigens nur 37 Byte).
Da wir 5,798,312 Wikipediaseiten und 165,913,569 Links haben kommen zu den obigen ca. 3 GB also nochmals 8,413,882,169 Byte hinzu. Eigentlich ein bisschen mehr, weil Sonderzeichen høhere „Betriebskosten“ haben, aber in der Summe sind das dann ungefaehr 11 GB.

Mhm … 11 GB das wird zwar knapp, aber so viel habe ich eigentlich. Warum kommt der Computer aber schon nicht mehr klar, wenn ich nur 10 Dateien eingelesen habe?
Ohne lange Rede: die Links sind in Sets (das ist sowas wie ’ne Liste ohne doppelte Objekte) angeordnet und davon habe ich natuerlich pro Titel eins. Insgesamt ist dann alles in einem einem sogenannten „Dictionary“ sortiert, damit ich zu jedem Titel leicht die zugehørigen Links finde (wie eben in einem Lexikon). Solche uebergeordneten Strukturen haben natuerlich auch Betriebskosten zusaetzlich (!) zu denen der einzelnen Elemente die in diesen Strukturen „aufbewahrt“ werden. Aber anders als bei den „primitiven“ Objekten wie oben beschrieben steigen die Betriebskosten in Abhaengigkeit von der Anzahl der Elemente die sich darin befinden. Klar, der gesamte Speicherbedarf eines Wortes ist abhaengig von der Anzahl der Buchstaben, aber das ist die „Nutzlast“. Die „Betriebskosten“ des Wortes sind davon unabhaengig. Und das ist bei den uebergeordneten Strukturen anders (weil die komplizierter sind und auch kompliziertere Operationen erlauben).

Zur besseren Veranschaulichung stelle man sich einen Gueterzug der Farbe transportiert vor. Alle Links die zu einem Titel gehøren entsprechen einer Farbe. Besagte Sets sind dann ein Tankwaggon, die jeweils nur eine Farbe enthalten. Wenn ich mehrere Tankwaggons habe, dann fallen die Betriebskosten (Wartung, oder Versicherung) pro Stueck an. Habe ich weniger Farbe, benutze ich einen kleineren Tankwagon, der geringere Kosten hat. Die Lokomotive (welche wiederum Betriebskosten hat) nun zieht alle Tankwaggons. Habe ich nur ein paar, benutze ich eine kleinere Lokomotive (mit geringeren Kosten), als wenn der Gueterzug so lang ist wie in Sibirien.

Und der Speicherbedarf dieser uebergeordneten Strukturen entwickelt sich selbst ohne die „Nutzlast“ dramatisch! Die „Waggons“ in denen sich die Links befinden benøtigen in ihrer kleinsten Form (also ohne Nutzlast, wenn ein Titel keine Links enthaelt) bereits 224 Bytes. Bei den ca. 6 Millionen Titeln macht das also mindestens (!) nochmal 1.3 GB. Und nun kommen wir in Regionen, wo mir der Speicher ausgeht.

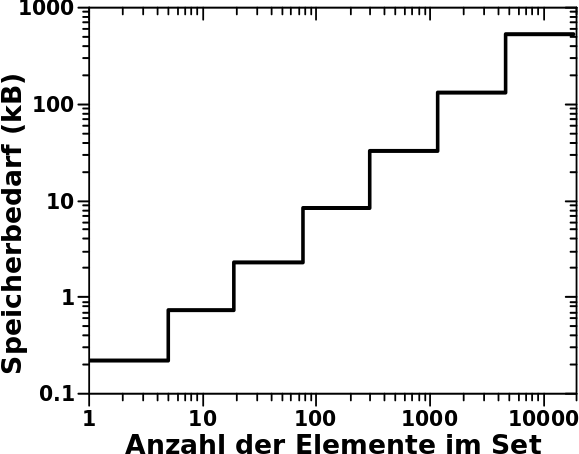
Aber eigentlich braucht die Anordnung in Sets deutlich mehr, denn beim Maximum der Verteilung bzgl. der Anzahl der Links pro Titel, beansprucht ein Set bereits 736 Bytes Speicherbedarf an „Betriebskosten“. 736 Bytes braucht ein Set auch dann, wenn es 18 Elemente hat, aber ab 19 Elementen braucht es 2272 Bytes. Insgesamt sieht das dann so aus:

Puuuuh … das geht linear, nochmal Glueck gehabt … … … Oopsie, das sind ja doppeltlogarithmische Achsen! … … … Ach du meine Guete! Der Anstieg ist ja positiv! Damit wird ja der Exponent des maechtigen Gesetzes grøszer Null!

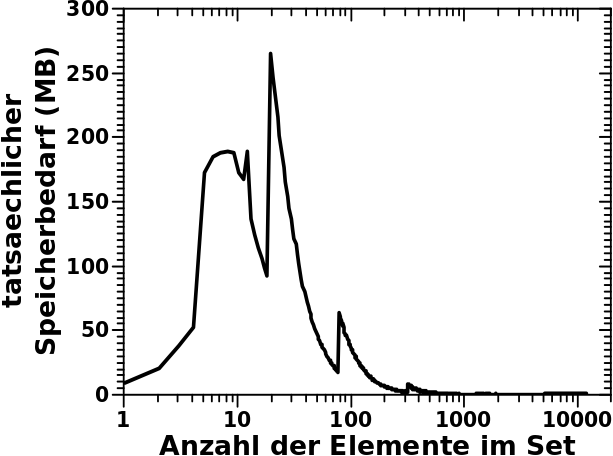
Lange Rede kurer Sinn: die vormals betrachtete, oben verlinkte, Verteilung der Anzahl der Links fuer alle Titel muss mit dem hier dargestellten Speicherbedarf _multipliziert_ werden. Das sieht dann so aus:

Mist! Die Ordinate ist linear und in Megabyte.

Erst jetzt ergibt das Integral unter dieser Kurve den tatsaechlichen Speicherbedarf dieser Ueberstruktur von Sets welche besagte Links enthalten: 10,962,695,936 Byte also ca. 11 GB die zu den obigen 11 GB noch dazu kommen. So viel Speicher habe ich nicht. Die „Lokomotive“ (das „Dictionary“), also die oberste Ordnungsstruktur, braucht dann bei ca. 6 Millionen Elementen nochmals 300 MB. Aber das faellt dann kaum mehr ins Gewicht.

Ich fasse zusammen. Der Speicherbedarf der eigentlichen „Buchstaben“ aller Titel und Links betraegt nur 3 GB. Aber die Verwaltung all dieser Buchstabenobjekte verursacht (in Python) „Betriebskosten“ von 8 GB. Die Strukturen in der die ganzen Objekte nun zusammengefasst sind verursacht dann nochmals „Betriebskosten“ in Høhe von weiteren 11 GB.
Kein Wunder, dass mein Computer da keine Lust drauf hat.

Wie ich dieses Problem løste stelle ich beim naechsten Mal vor. Denn die Løsung ist echt cool (weil so elegant) und erlaubte mir ueberhaupt erst das Gesamtproblem (die Erforschung des Linknetzwerkes) derart umzuformulieren, dass ein Computer das (schnell) løsen konnte.

Ach so … wenn ich hier 22 GB zusammenrechne, wie komme ich denn auf die 4.1 GB, die ich ganz oben erwaehne. Nun ja, wenn ich das alles auf der Festplatte speichere, dann wird die Struktur serialisiert. Dabei werden strukturierte Daten in einen seriellen Datenstrom „umgewandelt“ fuer die Speicherung. Darauf kann ich dann natuerlich nicht arbeiten.
Ich kønnte mir denken, dass viele von den „Betriebskosten“ gespart werden kønnten, indem man einen Teil des seriellen Datenstroms bspw. als „ab hier keine Zahlen sondern nur Wørter“ definiert (anstatt das fuer jedes Wort einzeln zu machen). Wenn das wieder zurueck „uebersetzt“ (de-serialisiert) wird, dann sieht der Algorithmus das und „baut“ daraus die richtigen Wortobjekte.
Aber das sollte alles als Spekulation gesehen werden, denn ich habe eigentlich gar keine Ahnung was da wirklich passiert.