Søren in Norwegen

Ausgehend von Kevin Bacon war der urspruengliche Plan das Linknetzwerk der Wikipedia zu untersuchen.
Dies ist im Grunde ein universelles (im Sinne von Universum) Problem — Die Beziehung von Informationen zueinander. Das habe ich dann gleich erstmal massiv auf Erdwissen eingeschraenkt welches sich in der (westlichen) Wikipedia befindet. Damit konnte ich das universelle Problem auf ein Sprachproblem reduzieren.
Das war aber immer noch zu viel, denn die Texte enthalten unheimlich viel Information, die im Sinne der Fragestellung „unbrauchbar“ ist. All das habe ich weggeschmissen und zurueck blieben die Titel von Wikipediaseiten und welche anderen Wikipediaseiten diese zitieren.

Das Wichtige an einem solchen Netzwerk sind nun aber nicht die Anzahl der „Knotenpunkte“. Ein Elefant hat deutlich mehr Neuronen als ein Mensch und dennoch sind es Fuszstapfen des Homo Sapiens auf dem Mond.
Nebenbemerkung: Gehirne sind urst krass kompliziert; bspw. haben grøszere Tiere im Allgemeinen auch grøszere Neuronen (die brauchen also mehr Platz). Und auch die Struktur des Gehirns (die Runzeln) oder in welchem Teil des Gehirns sich die Neuronen befinden ist wichtig. Und ich tu mal so, als ob es Vøgel nicht gibt.

Ganz generell ist also nicht die Menge der Knoten ausschlaggebend, sondern wie viele Verbindungen es zwischen den Knoten gibt. Selbst wenn ueber das Netzwerk jeder Punkt erreicht werden kann, so dauert es laenger, je mehr „Zwischenstops“ bei anderen Knoten man unterwegs einlegen muss. Oder anders gesagt: wer schaut sich schon die zweit oder gar dritte Seite mit den Sucherergebnissen an?
Diese Anzahl der Schritte bezeichnete ich am Anfang der Serie als „Linklevel“.

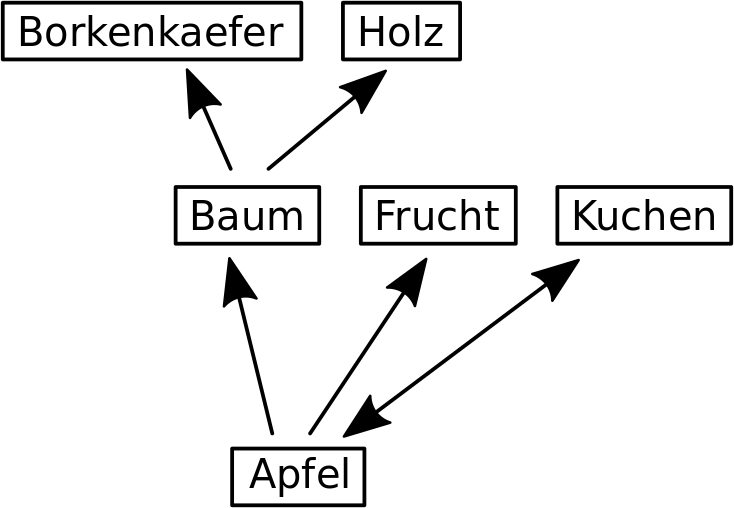
Zur Veranschaulichung nehme man dieses ausgedachte Beispiel:

Von Apfel (Linklevel 0, da das der Ursprung ist) komme ich direkt zu Baum, Frucht und Kuchen. Von Apfel aus gesehen liegen diese drei also auf Linklevel 1. Im Beispiel geht das Netzwerk bei Frucht nicht weiter. Von Baum aber geht es zu Borkenkaefer und Holz. Diese Beiden liegen von Apfel aus gesehen auf Linklevel 2 und von Baum aus gesehen auf Linklevel 1. Letzteres ist (erstmal) nicht von Interesse, denn hier interessiert uns nur Apfel und Baum wird separat untersucht.
Kuchen verweist nun zurueck auf Apfel. Das ist das, was ich spaeter „Selbstreferenz“ nennen werde, denn das ist ja prinzipiell auch von Interesse: wie entwickelt sich die Selbstreferenz je „weiter“ man weg ist vom Urpsrung? Natuerlich liegt fuer Kuchen der Apfel ebenso auf Linklevel 1 und via Apfel erreicht man dann von Kuchen aus die anderen Elemente (nur jeweils ein Linklevel høher). Auch dies wird in der Analyse separat betrachtet; ich erwaehne das nur, weil das aus dem Beispiel „heraus faellt“.

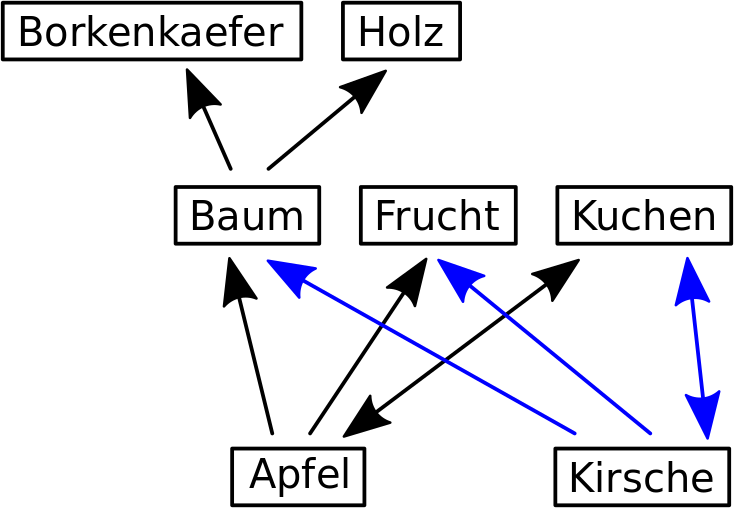
In einem zweiten Beispiel kommt Kirsche hinzu:

Das ist das Gleiche wie bei Apfel, nur von Kirsche aus gesehen ist Apfel auf dem selben Linklevel wie Holz (Linklevel 2) denn diese beiden „kommunizieren“ via den Knoten Kuchen. Umgekehrt gilt das natuerlich genauso.
Ich erwaehne dies, weil das Linknetzwerk absolut das Selbe (!) ist, trotzdem ein anderer Knoten als Ursprung genommen wurde.

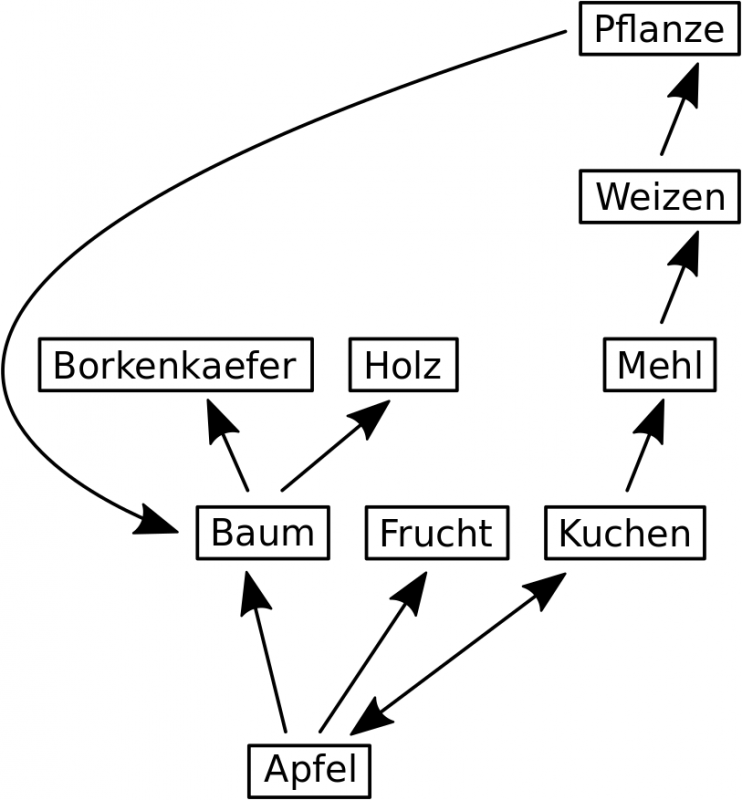
Jetzt noch ein drittes Beispiel:

Von Apfel komme ich via Kuchen, Mehl und Weizen zu Pflanze. Von Pflanze komme ich dann zurueck zu Baum. Damit wuerde Baum (von Apfel aus gesehen) auf Linklevel 1 und Linklevel 5 liegen. Das wird aber ignoriert, weil ich sonst in Schleifen gerate, aus denen ich nicht heraus komme. Dadurch, dass Baum bereits auf Linklevel 1 „besprochen“ wurde ist das auch gerechtfertigt denke ich.

Ich habe das aus zwei Gruenden (nochmals) so ausfuehrlich beschrieben. Zum Einen, um nach all den vorhergehenden Analysen und Diagrammen das urspruengliche Problem wieder in Erinnerung zu rufen. Zum Anderen sieht man hieran, dass ich das Sprachproblem „mathematisieren“ konnte. Denn wie man an den Beispielen sieht, faellt das Kevin-Bacon-Problem in das Gebiet der Graphentheorie.
Von Letzterer habe ich keine Ahnung. Das hindert mich aber nicht daran, ganz praktisch und pragmatisch an die Sache heran zu gehen und eine Løsung zu finden, die gut genug fuer das ist, was ich eigentlich wissen will.

Damit genug fuer heute.