Søren in Norwegen

Die verstørenden „Hundebilder“ von DeepDream sind ja sicherlich bekannt. Bekannt ist auch dass das in der „offiziellen Berichterstattung“ vehement natuerlich nicht als Kunst angesehen wurde. Meist mit dem Hinweis, dass der Algorithmus das Konzept des Hundes, des Bildes, des Hundes im Bild usw. usf. gar nicht _versteht_. Oder anders: ein „richtiger“ (vulgo: menschlicher) Kuenstler begreift ein Konzept und erschafft darauf aufbauend seine Kunstwerke. Als Beispiel faellt mir dazu Warhols Marilyn Diptych ein.

Und ehrlich gesagt, ich gehe da mit.

Andererseits erwarte ich von ’nem Schulkind auch nicht, dass es mir die Formeln des harmonischen Oszillators in quantenmechanischer Betrachtung herleiten kann.
Aber ich kann das auch nicht ohne Weiteres. Ich muesste mir das vorher nochmal anzuschauen. Mit „anschauen“ meine ich natuerlich nicht nur den harmonischen Oszillator an sich, sondern auch die vielen Konzepte und Sachen „drumherum“, die man braucht um das zu … verstehen.
Und damit bin ich wieder beim Schulkind, denn um die Konzepte der Quantenmechanik zu verstehen muss ich erstmal sooooo viele andere Konzepte begriffen haben. Nicht nur Analysis und Vektorrechnung, sondern auch Addition, Multiplikation und sogar noch „tiefer“ hinab gehend, den Unterschied zwischen Symbolen und deren Bedeutung wenn die zu neuen, anderen Symbolen zusammengesetzt sind. Letzteres ist natuerlich das was wir im Allgemeinen als „Lesen lernen“ bezeichnen. Und mit dem Lesen, lernen wir auch oft genug das Schreiben. Und zack, kaum kønnen sie schreiben, denken sich manche Kinder ihre eigenen Geheimschriften aus.
Aber nicht nur Kinder erfassen das Wesen von Symbolen und machen damit neue Sachen, sondern auch Erwachsene. So stammen das lateinische, das etruskische, das gotische, das glagolitische, das kyrillische (und vermutlich noch ’n paar andere) Alphabet vom griechischen Alphabet ab.

Das ist Symbolmanipulation, welche den Charakter, das Wesen der Symbole, erhaelt aber etwas Neues dabei schafft.

Und das kønnen mittlerweile auch Computer. In dem Artikel wird darauf eingegangen, wie man einem Cimputer beibringen kann, das Konzept von (Schrift)Symbolen zu erkennen und darauf aufbauend neue (Schrift)Zeichen mit dem selben Wesen zu erfinden. Und Bild 7 ist schon ziemlich beeindruckend.

Klar, das ist noch urst weit weg von Warhols Werk, aber die Autoren des verlinkten Artikels schreiben zu Recht:

Human cultures produce many such symbol systems, including gestures, dance moves, and the words of spoken and signed languages. As with characters, these concepts can be learned […]

Und zwar offensichtlich nicht nur von Menschen, sondern auch von Computern. Und die zwei Fragen die verbleiben sind: Was meinen die Journalisten eigentlich mit „verstehen“? und Wann geben wir zu, dass wir genuegend Sachen genauso wenig „verstehen“, aber trotzdem damit umgehen und darauf unsere Leben und unsere Gesellschaft aufbauen?

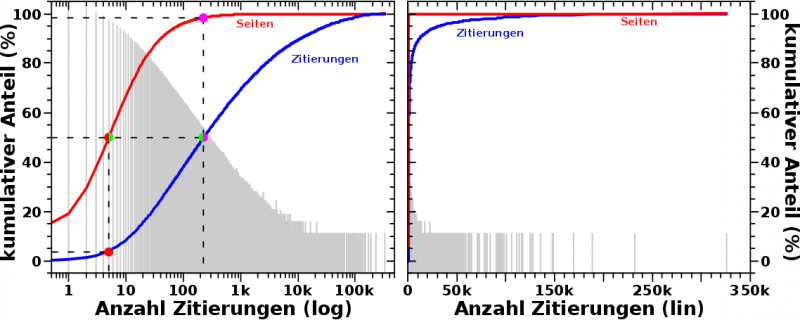
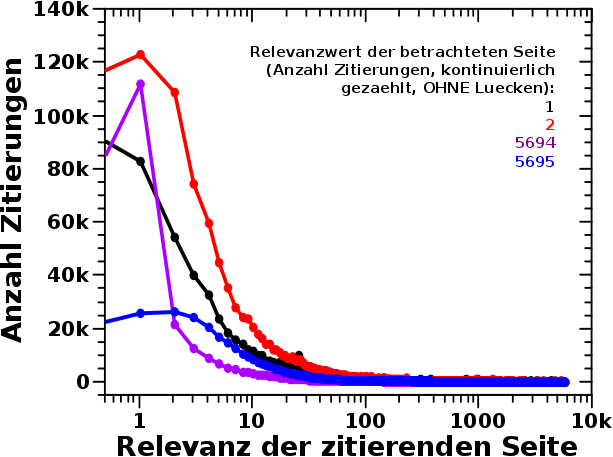
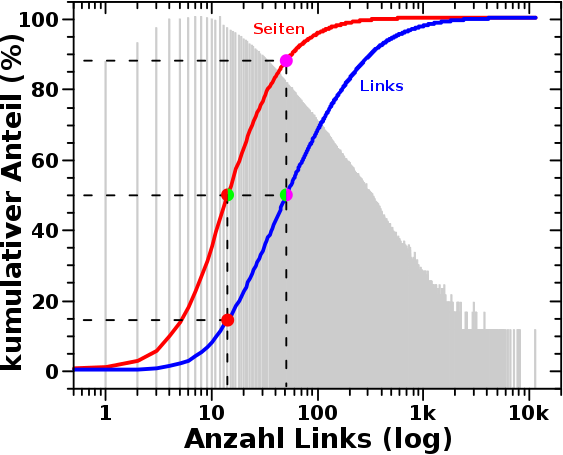
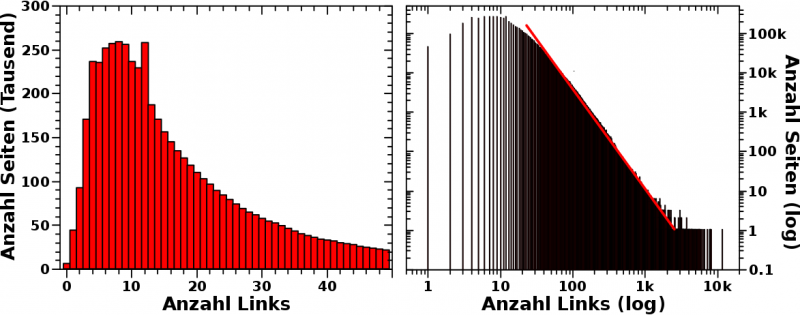
Kurze Wiederholung, weil es etwas komplizierter ist: beim letzten Mal stellte ich vor, dass sich die Relevanz von Wikipediaartikeln im Wesentlichen dadurch ausdruecken laeszt, indem man zaehlt wie oft ein Artikel zitiert wird. Der Einfachheit halber nenne ich hier Wikipeidaseiten mit kleinen Relevanzwerten „irrelevant“ (mit Anfuehrungszeichen). Das bedeutet nicht, dass die irrelevant (ohne Anfuehrungszeichen) sind.
Desweiteren stellte ich fest, dass die Wikipediartikel an den beiden Enden der Relevanzskala (die Artikel mit den kleinsten bzw. grøszten Relevanzwerten) vor allem von „irrelevanten“ Seiten zitiert werden. Daraus folgte, dass zumindest fuer die zwei meistzitierten Artikel die Relevanz nur deswegen zustande kommt, weil es die „irrelevanten“ Seiten gibt.
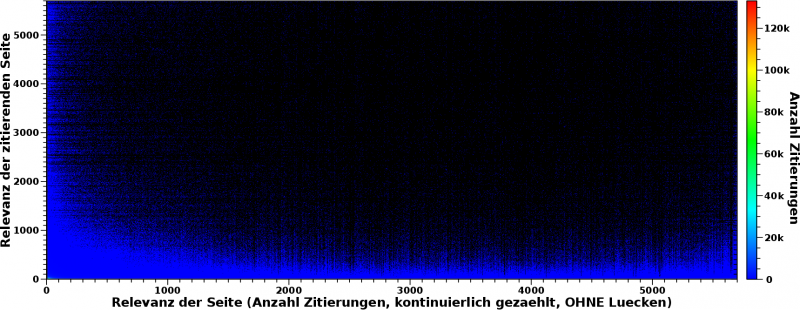
Das waren aber nur vier Beispiele und ich setzte mich mal hin und schaute mir das fuer _alle_ Wikipediaseiten an. Dies hier ist das Ergebnis:

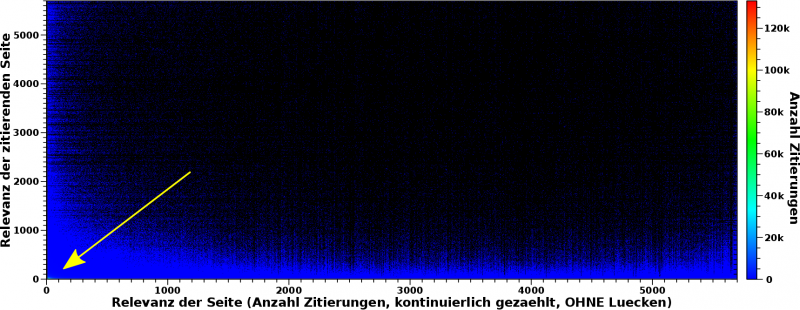
Wenn das Bild geklickt wird, dann wird das grøszer.

Was sieht man hier eigentlich? Die Abszisse repraesentiert den oben erwaehnter Relevanzwert einer Seite. Bis 2075 Zitierungen entspricht das der Anzahl der Zitierungen die eine Seite erhalten hat. Danach weichen die Relevanzwerte von der Anzahl der Zitierungen ab. Der Grund ist, dass die Werte der Abszisse das Resultat einer Abbildung einer Grøsze mit ungleicher „Schrittweite“ (Anzahl der Zitierungen) auf eine Grøsze mit konstanter „Schrittweite“ (Relevanzwert) ist. Ein kurzes Beispiel: es gibt keine Seite die 2076 mal zitiert wurde aber 2 Seiten die 2077 mal zitiert wurden. Der Relevanzwert zaehlt also „OHNE Luecken“.
Von der Bedeutung aendert sich aber nichts: je mehr Zitierungen eine Seite hat, desto relevanter ist diese (wohl) und entsprechend grøszer ist der Relevanzwert.

Die Ordinate repraesentiert im Wesentlichen die gleiche Grøsze, aber fuer die zitierende Seite.

Der Farbwert entspricht nun wie oft Seiten gefunden wurden, die einen bestimmten Relevanzwert haben und von einer (anderen) Seite mit einem (anderen) bestimmten Relevanzwert zitiert wurde.
Wenn also Seite A drei mal zitiert wurde von drei anderen Seiten die selber drei, elf und siebzehn mal zitiert wurden, dann zaehlt der Wert bei den „Koordinaten“ (3, 3), (3, 11) und (3, 17) ein mal hoch.
Wenn nun Seite B auch drei mal zitiert wurde, von Seiten die drei, sechs und sieben mal zitiert wurde, zaehlen die Werte bei den entsprechen „Koordinaten“ eins hoch. Der Wert bei (3, 3) ist nun zwei.
Diese Zaehlung habe ich nun fuer alle Wikipediaseiten gemacht und tritt fuer eine „Koordinate“ kein „Ereigniss“ auf, so bleibt das „Pixel“ fuer diese Koordinate schwarz.

Achtung: das obige Bild ist eine quadratische Matrix! Aufgrund gegebener Limitierungen in der Praesentation habe ich mich aber entschieden die Abszisse „laenger“ zu machen als die Ordinate.
Nochmal Achtung: Das ist zwar eine quadratische, aber keine symmetrische Matrix! Auch wenn auf den Achsen beide Male Relevanzwerte dargestellt sind, so ist die Bedeutung geringfuegig anders (wie oben beschrieben).

Wir sehen im Bild nun, dass das ueberwiegend schwarz ist. Bei den meisten Koordinaten zaehlt also nix hoch, weil es keine Seiten mit dem jeweiligen Relevanzwert gibt, die zitiert werden von Seiten mit dem (anderen) jeweiligen Relevanzwert. Schaut man genau hin, ist da „Rauschen“ drin. Ich komme da spaeter drauf zurueck.

Desweiteren sieht man, dass sich alles an der linken und unteren Kante abspielt — der blaue „Saum“. Das ist wichtig, denn dies ist eine Bestaetigung der beim letzten Mal getroffenen Aussage. Egal wie wichtig eine Seite ist (Wert auf der Abszisse), diese erhaelt ihre Wichtigkeit vor allem dadurch, weil sie von „irrelevanten“ Seiten zitiert wird (Wert auf der Ordinate). Das ist das blaue Band am unteren Rand.

Das blaue Band am linken Rand besagt nun, egal wie wichtig eine Seite (Ordinate) ist, diese zitiert vor allem „irrelevante“ Seiten (Abszisse). Und das ist krass!
Warum ist das krass? Nun ja, die erste Aussage (Wichtigkeit nur durch die Zitierung von „irrelevanten“ Seiten) ist ja eindeutig. Aber das Ganze geht noch weiter! Denn die zweite Aussage bedeutet, dass selbst die relevantesten Seiten ueber irrelevante Sachen schreiben (weil man ja zitieren muss worueber man schreibt).
Und DAS bedeutet dann nicht nur, dass relvante Seiten nur durch die Zitierungen irrelvanter Seiten relevant werden, sondern dass es relevante Seiten gar nicht geben wuerde, wenn diese nicht ueber „irrelevante“ Seiten schreiben kønnten!

DAS ist so krass, denn dies setzt der Relevanzdiskussion ein Ende und die Inkludisten sind die eindeutigen Gewinner!

Das ist das Resultat. Nun ist’s aber nicht ganz so einfach … und warum geht die Farbskala eigentlich bis ueber 120-tausend Ereignisse, wenn im Bild entweder alles schwarz oder blau (ein paar tausend Ereignisse) ist?
Nun ja, deswegen ist da ein Pfeil im Bild.

Ich zoome mal rein:

AHA! Da wird’s rot. Im Bereich bis zu Relvanzwerten von 100 passiert alles … bzw. nix, denn der schwarze Balken bei einer Relevanz von Null liegt natuerlich daran, dass diese Seiten null mal zitiert werden … aber ich schwoff ab.
Koordinaten fuer Seiten die ein bis zehn mal zitiert werden, von Seiten die selber null bis zwei Zitierungen haben sind im gelb/roten Bereich. Das sind also 10 mal 3 mal 100-tausend „Ereignisse“ die sich dort „versammeln“. Diese Gruppe ist umgeben von einem deutlich breiteren, gruenen „Halo“ welche Ereignisse mit Zaehlungen bis ca. 60-tausend beinhaltet.
Die Vielzahl der „irrelevanten“ Seiten die sich selber zitieren fuehrt zu so krass vielen Zitierungen (Ereignissen), dass das was in diesem Bereich angehaeuft ist vom absoluten Wert alles andere in den (blauen) Schatten stellt. Und weil die „Ausdehnung“ dieser Gruppe so klein ist, sieht man das im ersten Bild nicht.

Das ist jetzt natuerlich ein Problem in Bezug auf die obigen Aussagen. Die schiere Menge an Zitaten von (und an) „irrelevante(n)“ Seiten erdrueckt das Signal der Seiten mit grøszeren Relevanzwerten.

Aber zum Glueck ist dies mit einer simplen mathematischen Transformation sehr leicht in Betracht zu ziehen: jede Spalte muss normiert werden.
Das hørt sich jetzt fancy-pancy an, was das bedeutet ist aber, dass alle Werte in einer Spalte durch den grøszten Wert dieser Spalte geteilt werden. Besagter grøszter Wert wird dann natuerlich zu 1. Das Gute ist nun, dass ALLE grøszten Werte ALLER Spalten den Wert 1 haben. Dadurch wird das „Gewicht“ von der Farbskala genommen und Spalten mit groszen Relevanzwerten kønnen mit Spalten mit kleinen Relevanzwerten verglichen werden. Dabei ist natuerlich immer im Hinterkopf zu behalten, dass dies relative Vergleiche sind, im Gegensatz zum Vergleich der absoluten Werte in den obigen beiden Bildern.
Und so sieht das dann aus:

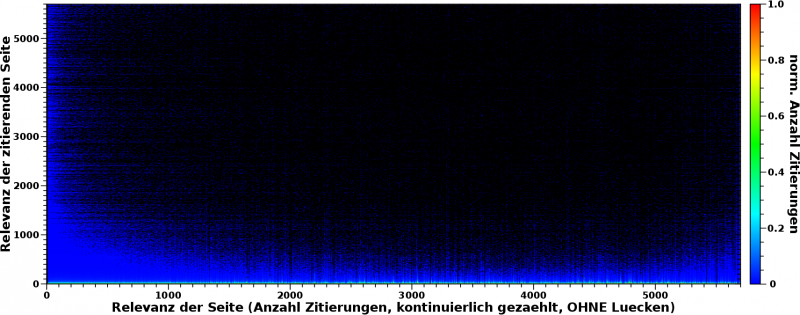
Haeh? What? Das ist doch das Gleiche! … Nun ja, nicht, wenn man ganz genau auf den unteren Rand schaut (ACHTUNG: die Ordinate geht nur noch bis 200 „Ereignisse“):

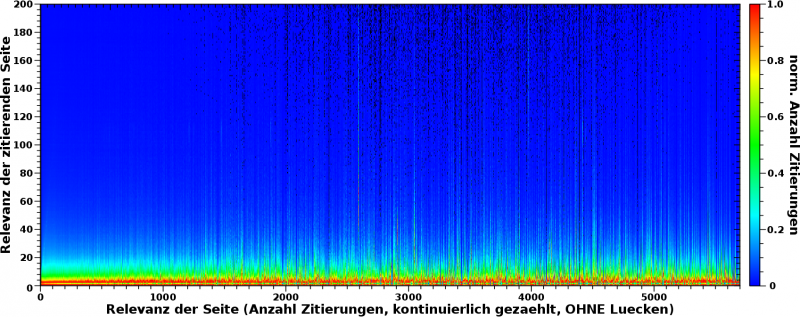
AHA! Das sieht doch schon ganz anders aus. Durch die Normierung wird (wie vorgesehen) der erdrueckende Anteil der Ereignisse bei kleinen Relevanzwerten irrelevant (tihihi). Das Resultat ist nun das rot gruene Band am unteren Rand. Dieses haelt die obige (erste) Aussage aufrecht: fuer ALLE Seiten, vøllig unabhaengig davon wie grosz (oder klein) die absolute Anzahl der Zitierungen ist, gilt, dass diese hauptsaechlich von „irrelevanten“ Seiten zitiert werden.
Das ist zwar das Selbe wie oben schon erkannt, aber es ist gut, dass diese Kontrolle nicht zu einem anderen Ergebis gefuehrt hat.

Aufmerksamkeit møchte ich richten auf die Tatsache, dass ein mal zitierte Seiten (Relevanzwert = 1, auf der Abszisse)  interessanterweise weniger haeufig andere Seiten zitieren als null mal bzw. drei mal zitierte Seiten. Dies drueckt sich in dem duennen gruenen Streifen parallel zur Abszisse aus, der eingequetscht ist zwischen den roten Streifen bei Relevanzwerten (der zitierenden Seiten, also auf der Ordinate) von null bzw. zwei.
Man sieht das auch bereits in den nicht normierten Daten im obigen Bild. Dort sieht man dann auch einen Grund: der Wert bei der Koordinate (1, 1) hebt sich deutlich hervor im Vergleich zu den Werten bei (1, 0) bzw. (1, 2).
Dies wiederum deutet darauf hin, dass meine Erklaerung des „im Kreis zitieren“ vom letzten Mal …

[s]ozusagen wenn Hintertupfingen Vordertupfingen zitiert, weil’s das Nachbardorf ist (und umgekehrt), aber beide von keiner anderen Seite zitiert werden

… schon in die richtige Richtung geht fuer viele dieser Seiten. Denn wenn die ihr eines Zitat fuer die „Nachbardorfseite“ verbrauchen und umgekehrt, dann fehlt das „Signal“ natuerlich an anderer Stelle.

Dies wiederum waere dann aber auch ein Hinweis auf (mehr oder weniger) tataechliche Nichtrelevanz, da diese Seiten dann ja in keinem Diskurs teilnehmen, sondern nur eine Nabelschau sind. Ich persønlich wuerde die aber trotzdem drin behalten.

Genug dazu … wie sieht das nun mit der zweiten Aussage aus? Ueber was schreiben die (nicht nur relevanten) Seiten eigentlich? Dafuer muss man natuerlich alle Zeilen normieren und das sieht dann so aus:

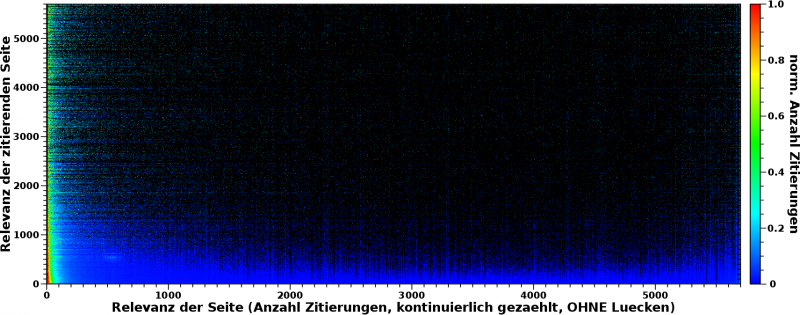
Aha! Ein bunter Streifen, der sich an die Ordinate schmiegt. Wenn man rein zoomt, dann sieht das so aus:

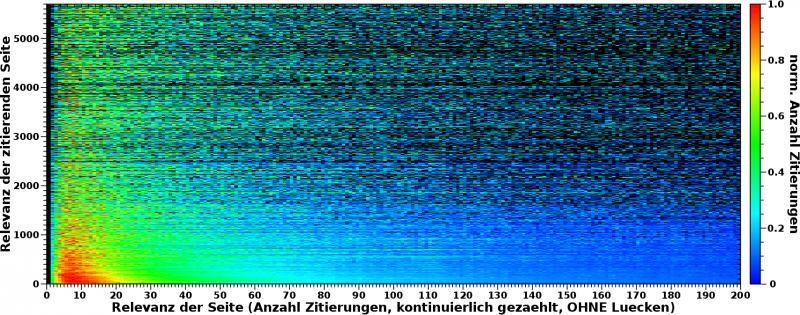
Im Allgemeinen bleibt also auch die zweite Aussage bestehen: ALLE Seiten zitieren hauptsaechlich „irrelevante“ Seiten. Das ist die Bedeutung des gruen-roten Bereichs am linken Rand. Aber das muss etwas genauer betrachtet werden.

Zum Ersten ist das, anders als beim obigen Fall, kein eindeutiges „rotes Band“ (parallel zur Ordinate in diesem Fall). Das „duennt aus“ je grøszer die Relevanzwerte der zitierenden Seite wird. Dies wiederum bedeutet, dass das „Signal“ bei høheren Relevanzwerten (auf der Abszisse) grøszer werden muss zu høheren Relevanzwerten auf der Ordinate. Nun sieht man das im Gesamtbild aber wieder nicht, weil das Gesamtsignal bei kleinen Relevanzwerten von vielen Seiten stammt, waehrend es bei groszen Relevanzwerten von wenigen, oft nur einer Seite „generiert“ wird. Die angesprochene Beobachtung geht also im „Rauschen“ unter.

Aber tatsaechlich, schaut man sich mal die Ecke bei den 1000 grøszten Relevanzwerten an …

… dann scheint sich da Information zu verstecken! In den zeilenweise normierten Daten geht das „Rauschen“ oft in den blauen und gar gruenen Bereich (manchmal gar in den roten). Hier ist also noch „was zu holen“.
Aber darum soll es beim naechsten Mal gehen: wie man das Mehr an Information aus den Daten kitzeln kann :)

Zum Zweiten liegt das Maximum des „roten Bereichs“ nicht bei Relevanzwerten von 1 oder 2 sondern eher bei Relevanzwerten von 5, 6 und 7. Dies ist zum Glueck einfach zu erklaeren.
Seiten mit den kleinsten Relevanzwerten werden zwar total gesehen am haeufigsten zitiert (die Anzahl der Seiten die nur ein mal zitiert werden ist grøszer als fuer alle anderen Relevanzwerte), aber wenn eine Seite mit Relevanzwert 1 ihr eines Zitat erhalten hat, dann ist diese Seite „verbraucht“. Die naechste Zitierung muss also zu einer anderen Seite mit Relevanzwert 1 gehen. Bis wir durch sind mit denen. Dadurch „verschmiert“ sich das Gesamtsignal fuer alle Seiten mit Relevanzwert ueber den kompletten Wertebereich.
Hingegen wenn eine Seite mit Relevanzwert 6 eine Zitierung bekommt, dann kann die noch fuenf weitere Male zitiert werden. JA, die Anzahl der Seiten mit Relevanzwert 6 ist geringer, aber das Produkt aus erhaltenen Zitaten und Anzahl der Seiten ist grøszer. Bei Relevanzwerten ueber sieben ist’s dann aber wieder so, dass die Anzahl der Seiten so stark abnimmt, dass besagtes Produkt wieder kleiner wird.
Das sieht man uebrigens auch im Bild mit dem „reingezoomten“ Bild mit den total Zahlen und deswegen erscheint das Maximum des „roten Bereichs“ der (zeilenweise) normierten Daten eher dort.

Dieses Wechselspiel aus totalen und normierten Zahlen bzw. vielen Seiten und vielen Zitierungen (bzw. dem Produkt aus beiden) muss alles im Kopf behalten werden waehrend der Interpretation dieser Diagramme. Ich gebe zu, dass dies nicht immer einfach ist. Ich sasz oft laenger da, ohne dass mir die Erklaerungen „ins Gesicht gesprungen“ ist. Vielmehr musste ich alle Gegebenheiten auseinanderklamuesern, mir genau ueberlegen was die Normierung (oder die Achsen, oder der Farbwert) eigentlich bedeutet, und total aufpassen, dass mir da nix durcheinander kommt um das Signal zu interpretieren und die Zusammenhaenge zu erkennen.
Und das ist einer der Gruende, warum ich das so toll finde. Einfach, kann ja jeder :)

Die Darstellung der kumulativen Anteile der Anzahl Links pro Seite erinnerte mich, dass ich das bei den Zitierungen nur indirekt und mit Worten machte. Hier nun als Graph:

Im Hintergrund habe ich wieder die Verteilung reingelegt, wieviele Seiten wie oft zitiert wurden. Die rote Kurve stellt dann dar, wie vielen Seiten das insgesamt bis zum gegebenen Argument entspricht (in Prozent). Dito fuer die Zitierungen (blaue Kurve). Wie der Graph zu lesen ist erklaerte ich beim letzten Mal, ich markierte wieder die 50 % Werte.
Verglichen mit den Kurven beim letzten Mal ist der Unterschied zwischen den Anteilen VIEL krasser! Das sieht man noch deutlicher im Diagramm auf der rechten Seite, wo der Anteil der Seiten sich praktisch an die Ordinate anschmiegt und dann „sofort“ bei 100 % ist. Das ist eine Sache, die bei der Beschreibung mit Worten gar nicht soooo dolle rueber kam.
Kleine Abschweifung: beide Diagramme enthalten die gleiche Information (oder gar die Selbe?). Aber erst durch die verschiedenen Abszissen wird man erst auf bestimmte Dinge aufmerksam.

Warum zeige ich das hier? Nun ja, davon abgesehen, dass das ’n cooles Diagramm ist, ist es auch wichtig fuer das was ich im Folgenden besprechen werde. Denn diese Darstellung brachte mich auf die Idee, dass man die beruehmt-beruechtigte Relevanz mglw. messen kann. Nicht dass ich denke, dass das irgendwen umstimmen wuerde, aber es ist mal interessant anzuschauen.

Die Grundlage der „Messbarkeit der Relevanz“ ist ganz einfach: ein Artikel ist relevant wenn er ein wichtiger Teil der Diskussion ist. Ein wichtiger Teil der Diskussion ist ein Artikel, wenn dieser oft zitiert wird. Wie oft ist oft? Das ist dann im Allgemeinen nicht mehr so einfach zu quantifizieren.
Aber das ist auch nicht wirklich nøtig, denn im Speziellen denke ich, dass ein Konsens darin gefunden werden kann, dass die paar Seiten (lila Punkt im linken Diagramm) die 50 % der Zitierungen (gruen/lila Punkt) auf sich vereinen mit Sicherheit relevant sind. Einfach aus der (messbaren und damit objektiven (?)) Tatsache, dass die so krass viele Zitierungen auf sich vereinen, obwohl es sich dabei um nur ein bisschen mehr als 1.5 % aller Wikipediaseiten handelt. Zur Erinnerung: hier hatte ich die 50 meistzitierten Seiten aufgelistet.

Damit stellt sich dann als naechstes die Frage: wer zitiert diese Seiten eigentlich so oft? Oder anders: „wer“ sorgt eigentlich dafuer, dass diese Seiten relevant werden (sind)? Und DAS ist messbar … wird aber ein dreidimensionales Datenfeld mit 32,433,025 Millionen Werten … aber ich greife vor.

Zunaechst einmal: wie kann das gemessen werden?
Nun ja, das ist (mehr oder weniger) ganz einfach. Ich habe fuer jede Seite die Zitate (vulgo Links zu anderen Wikipediaseiten). Nun gehe ich zum ersten Mal durch die Daten, schaue fuer jede Seite wie oft die von anderen Seiten zitiert wird und merke mir das. Damit habe ich nun ein Masz fuer die „Wertigkeit“, „Wichtigkeit“ oder eben „Relevanz“ einer Seite. Je mehr Zitierungen desto „relevanter“.
Dann gehe ich ein zweites Mal durch die Daten und fuer jede zitierte Seite merke ich mir dann, von welcher Wichtigkeit die Seite war, welche diese Zitierung ausgesprochen hat. Letzteres weisz ich ja vom ersten Durchgang.

Das muss ich zwar fuer jede Seite in Erfahrung bringen, aber die Information wird zusammengefasst in Gruppen nach ihrer Relevanz. Also bspw. wann immer eine Seite die fuenf Mal zitiert wurde von einer anderen Seite die drei Mal zitiert wurde zitiert wird, dann zaehlt der Zaehler dieser 3-5-Gruppe einen hoch. Damit habe ich 3596 mal 3596 Gruppen. Wie? Nur so wenige? Mindestens eine Seite wird doch deutlich mehr als 300-tausend mal zitiert. Die Erklaerung liegt darin (wie man im Diagramm auf der rechten Seite sieht), dass da ganz schøn viel „Luft“ zwischen den Balken mit groszer Anzahl an Zitierungen ist.

Lange Rede kurzer Sinn: der Relevanzwert entspricht der Anzahl der Zitierungen ohne Luecken. Dabei muss man dann im Kopf behalten, dass die Relevanzwerte von 0 bis 2075 tatsaechlich dem entsprechen wie oft eine Seite zitiert wurde. Hingegen entspricht der Relevanzwert 5695 der einen Seite, die mehr als 325-tausend mal zitiert wurde und der Relevanzwert von 5694 eben jener Seite die „nur“ ein bisschen mehr als 231-tausend mal zitiert wurde; usw. rueckwaerts is alle Luecken geschlossen sind.
Das ist gar nicht so verwirrend, wie es sich erstmal anhøren mag. Ich bilde nur die groszen Werte auf kleineren Werten nach einer gegebenen (determinischen) Zuordnungsfunktion ab. Im Wesentlichen zaehle ich nur etwas anders.

Auch wenn das eine deutliche Reduktion des Problems ist, so sind das dennoch die weiter oben erwaehnten 5695 mal 5695 = 32,433,025 Millionen Werte.
Als ich das das Erste Mal programmierte hackte ich nur kurz zusammen, was mir gerade in den Kopf kam. Die beiden Durchlaeufe brauchten zwei Tage. Dann merkte ich, dass ich einen Fehler gemacht hatte, korrigierte den und liesz das nochmal zwei Tage laufen.
Dann hatte ich die Idee, dass ich das Ganze ja gleich in eine Matrix schreiben kønnte. Die eine Dimension der Matrix ist die „Relevanz“ einer Seite (in ganzen Zahlen mit oben erwaehnter Zaehlung). Die andere Dimension ist die Relevanz der zitierenden Seite. Und der Wert eines Felds ist dann wie oft diese bestimmte „Gruppe“ in den Daten auftauchte. Der Code wure dadurch viel einfacher und leichter zu verstehen und mit dieser (grundlegend alles veraendernde) Modifikation brauchte das dann nur noch 15 Minuten anstatt 2 Tage.
Das mit der Matrix ist ja eigentlich eine naheliegende Idee und da haette ich auch gleich drauf kommen kønnen. Aber als ich anfing hatte ich noch keine klare und eindeutige Vorstellung davon, was ich eigentlich untersuchen wollte. Also ich hatte das schon, aber „nur“ in Worten. Mein Geist brauchte ein paar Tage um das intern zu mathematisieren. Aber dann ging’s fix :) … also zumindest das Datensammeln. Zu interpretieren was ich da eigentlich sehe dauerte dann noch einige Tage mehr.

Und so sieht das aus fuer alle (!) Seiten die ein bzw. zwei Mal (schwarze und rote Punkte) zitiert wurden und fuer die zwei Seiten mit den Relevanzwerten von 5694 bzw. 5695 (lila und blaue Punkte):

ACHTUNG: Die Linien sind nur zur Orientierung (der Richtung)! Es gibt keine Werte zwischen den ganzen Zahlen. Aber aufgrund der logarithmischen Abzsisse kann die Null nicht dargestellt werden und deswegen benøtigt es eine Orientierung der Richtung fuer den Verlauf vom Relevanzwert 1 zum Relevanzwert 0.
Fuer diese vier Beispiele sieht man, dass alle Seiten vor allem von „nicht relevanten“ Seiten zitiert werden. Fuer die selber „nicht relevanten“ Seiten bedeutet das mglw., dass die sich „im Kreis zitieren“. Sozusagen wenn Hintertupfingen Vordertupfingen zitiert, weil’s das Nachbardorf ist (und umgekehrt), aber beide von keiner anderen Seite zitiert werden.
Interssant ist, dass Seiten mit einem Relevanzwert von 1 vor allem von Seiten mit einem Relevanzwert von 0 zitiert werden, also von Seiten die ihrerseits NICHT zitiert werden.
Uebrigens tut das nix zur Sache, dass der høchste lila Punkt (von der am zweitmeisten zitierten Seite) deutlich høher ist als der høchste blaue Punkt. Das Integral unter der Kurve entspricht der Anzahl aller Zitierungen und die blauen Punkte sind zu groszen Relevanzwerten hin immer ueber den lila Punkten. Das sieht man aber in der linearen Darstellung nicht, weil die Werte unter 1000 liegen.
Die schwarzen und roten Punkte liegen da uebrigens nochmal drueber, denn alle Seiten die ein mal zitiert wurden sind ja viel mehr als die (buchstaeblich) zwei meistzitierten Seiten … oder anders: Kleinvieh macht auch Mist.

Bemerkenswert ist nun, dass auch die zwei meistzitierten (und damit die zwei relevantesten) Seiten am haeufigsten von „nicht relevanten“ Seiten zitiert werden. Wait! What? Das wuerde doch bedeuten, dass die nur deswegen relevant sind weil sie von „nicht relevanten“ Seiten zitiert werden! Was im Umkehrschluss bedeutet, dass die ganze Relevanzdiskussion fuer’n Arm ist, weil es die einen nicht ohne die anderen geben kann.

Aber das sind nur vier Beispiele. Fuer die Gueltigkeit dieser Aussage muss ich das fuer alle (oder zumindest die Mehrheit) der relevanten Seiten zeigen. Nun weisz ich aber aus Erfahrung, dass man nix mehr erkennt, wenn man fast 5700 Kurven darstellt. Ich kann das aber als Falschfarbenbild darstellen. Dazu aber mehr beim naeachsten Mal  … … … Na gut … hier schon mal ein Spoiler … tihihi:

Keine Sorge, das wird noch spannend :) .

Eine weitere „ancient probe“ im Ursprungssystem ist diese hier:

Ich flog ganz nahe ran und entdeckte, dass diese sogar eine Namensplatte hat. Leider ist die beschaedigt …

… und ich konnte nur „V…ger“ ausmachen. Unter diesem Namen finde ich im Informationsnetzwerk einen Zusammenfassung dieses Ereignis vor ein bisschen mehr als 1000 Jahren. Seltsam, ich dachte, dass da nix zurueckgeblieben waere. Wieauchimmer, ich lass V…ger hinter mir und fliege zum letzten Signal welches als „ancient probe“ im Scanner erscheint.

Im ersten Artikel zu den Zitierungen gab ich nur wørtlich (bzw. als Zahlen im Diagramm) an, wieviele (oder vielmehr wie wenige) Seiten so und so viel Prozent der Zitierungen ausmachen. Ungefaehr nur ein Drittel aller Seiten vereinen ueber 90 Prozent aller Zitierungen auf sich.

Fuer die Anzahl der Links sieht das aehnlich aus, diesmal aber als Diagramm (zur besseren Orientierung habe ich im Hintergrund die doppeltlogarithmische Verteilung vom letzten Mal herein gepackt, die hat aber keine zugehørige Ordinate!):

.oO(endlich mal keine Verteilung.)

Wie ist dieses Diagramm zu lesen?
Die Kurven stellen jeweils den aufaddierten Anteil aller Seiten (rote Kurve), bzw. aller Links, bis zum gegebenen Argument dar. Als Beispiel nehme man die zweifarbigen Punkte, welche bei jeweils 50 % verortet sind.
Der rot/gruene Punkt liegt bei 14 Links pro Seite und die Haelfte alle Seiten hat so viele oder weniger Links. Folgt man diesem Punkt nach unten, landet man bei ca. 15 % auf der blauen Kurve. Dies bedeutet also, dass 50 % aller Seiten, nur ca. 15 % aller Links auf sich vereinen.
Nun der gruen/lila Punkt. Dieser liegt bei 51 Links pro Seite. Man muss also alle Seiten mit 51 Links oder weniger zusammen nehmen um 50 % aller Links auf der Wikipedia (zu anderen Wikipediaseiten) zu bekommen. Dafuer muss ich aber fast 90 % aller Wikipediaseiten besuchen (lila Punkt auf der roten Kurve).

Umgekehrt bedeutet dies, dass nur ca. 10 % aller Seiten die Haelfte aller Links enthalten! Wiederum werden die Zahlen also von wenigen Seiten dominiert.

Dies hingegen macht eine einfache Abschaetzung der benøtigten Schritte fuer eine „Rundreise“ auf dem kompletten Linknetzwerk fuer mich nicht møglich. Ich schreibe „fuer mich“, weil es bestimmt mathematische Werkzeuge gibt, mit denen man das unter den gegebenen Umstaenden machen kann, aber die sind mir nicht bekannt.
Aus den vielen Seiten mit wenigen Links wuerde ich vermuten, dass man relativ viele Schritte per Rundreise braucht. Wenn man aber nur ein paar wenige Seiten mit vielen schon anfangs erreicht, dann sollte man nur wenige Schritte brauchen. Das hier sind also entgegengesetzte „Prozesse“.

Es sei denn, wenn die Ersteren vor allem sich selber und die Letzteren auch vor allem sich selber zitieren. Wenn also diese zwei Gruppen „unter sich bleiben“.
Aha! … Da muss ich doch glatt mal schauen ob ich da was rausfinden kann.

Deswegen genug fuer heute.

Ach so … Was fuer Seiten das sind, die extrem viele Links enthalten, hatte ich bereits hier besprochen. Und Seiten die keine Links haben werden (wie hier erwaehnt) in meinen Betrachtungen nicht rausgeschmissen wenn diese noch auf anderen Seiten zitiert sind. Drei Beispiele waeren Clematis marmoraria (natuerlicherweise zitiert auf Clematis), Serbian proverbs (zitiert auf Culture of Serbia), oder Third-party software component (zitiert auf Easy Chirp, Shareaza, Foobar2000 und 83 anderen Seiten).

Ich war mal wieder im Ursprungssystem. Eigentlich dachte ich ja, dass ich hier schon alles gesehen haette. Aber dann tauchten im Scanner pløtzlich drei Signale auf. Diese waren mit „ancient probe“ (und nix weiter) bezeichnet.

Cool! Ich kønnte schwøren, dass die bei meinem letzten Besuch noch nicht hier waren, aber da war mir auch nicht langweilig (weswegen ich das System beim letzten Mal nicht scannte).

Ich befand mich nahe des Ursprungsplaneten und besagte Objekte waren ganz schon weit weg von mir. Ich flog dennoch hin und das hier fand ich beim ersten Stop:

Nanu? Was war das denn? Gaaaanz tief unten im Keller des galaxisweiten Informationsnetzes fand ich heraus, dass es sich hierbei um eine mehr als tausend Jahre alte Forschungssonde handelt. Schon krass, mit was fuer kuemmerlichen Geraeten die Wissenschaftler damals Wissen schafften.

Von grøsztem Interesse bzgl. des Linknetzwerks ist die (durchschnittliche) Anzahl der Links pro Seite. Je grøszer diese Zahl ist, desto weniger Schritte brauche ich im Schnitt um das komplette Netzwerk „abzuschreiten“.

Deswegen schaute ich mir genau das mal an und die Verteilung …

… ueberraschte mich.

In der doppeltlogarithmischen Darstellung auf der rechten Seite sieht man (wieder), dass das Verhalten (wieder) ueber einen weiten Bereich mittels eines Potenzgesetzes beschrieben werden kann. Ich wuesste zwar immer noch keinen Mechanismus warum das so sein muesste, aber das ist ja von den Zitierungen bekannt.
Bei genauerer Betrachtung sieht man, dass die Anzahl der Seiten in Abhaengigkeit von der Anzahl der Links im Bereich zwischen ca. 100 und 500 Links etwas von der Geraden abweicht. Phaenomenologisch ist das in dem hiesigen Zusammenhang nicht relevant. Ich bin nur an einer Abschaetzung interessiert. Aber so eine kleine Diskrepanz ist auch, wie das Higgs-Boson entdeckt wurde (siehe Abbildung 1 in diesem Artikel).
Und Phaenomenologie … mhmmm … das kann manchmal auch eine der Intention komplett entgegengesetzte Reaktion zur Folge haben … tihihihi

Das unerwartete ist aber im linken Diagramm zu sehen. Wie bei allen vorherigen Verteilungen haette ich ein deutlich ausgepraegtes Maximum bei einem Wert erwartet. Aber das Maximum bei 8 Links „verschmiert“ sich zu 6 und 7 und 9 Links. Auch die Zaehlungen bei 4 und 5 bzw. 10 und 11 Links sind nur ca. zehn Prozent geringer als der Maximalwert … und 10 % Unterschied wuerde ich normalerweise in den bereits øfter erwaehnten Fehler-bei-Daten-aus-der-echten-Welt einordnen (zumindest wenn kein Trend zu erkennen ist) … ich wuerde das „Maximum“ also eher als Plateau von 5 bis 11 Links sehen.
Bei den Untersuchungen zu den Zitierungen stellte ich fest, dass extrem viele Artikel sehr selten zitiert werden. Ich gab ein paar Beispiele und dabei handenlte es sich um sehr oder relativ kurze Artikel. Da ich die mehr (mehr oder weniger) zufaellig auswaehlte, kann man das durchaus als repraesentativ ansehen. In einem kurzen Artikel gibt es natuerlich auch nicht so viele Gelegenheiten was anderes zu zitieren. Aus der Menge der (wenig zitierten) kurzen Artikel erklaert sich dann auch die grosze Anzahl der Artikel die 5 bis 11 Links haben.

Und dann kommt ganz unerwartet nochmal ein signifikanter „Ausschlag“ bei 12 Links! What the what? Das sieht aus als ob das so ’ne unbewusste, kollektive, psychologische Grenze ist: .oO(Ach jetzt habe ich 11 Links, einer geht noch) … ein kurioses Phaenomen.

Genug fuer heute.

Spike …

… ist einer von Snoopies Geschwistern und er wohnt in der Wueste in einer Wohngemeinschaft mit einm Saguarokaktus.

Spike war mir immer sympathisch. Er ist ein bisschen weltfremd, aber meist zufrieden mit seinem Leben fernab der Krach machenden Zivilisation.

Am Anfang ist mir das gar nicht so aufgefallen, aber Snoopies Geschwister interagieren fast nie mit den restlichen Charakteren.

Es wuerde mich nicht wundern, wenn das bei mir unterbewusst auch dazu beitraegt, dass ich Geschichten rund um die hochantropomorphisierten Hunde immer mit am besten fand :)

Der zweite Band (hier der Schuber) …

… kam ein Jahr nach dem ersten Band heraus. Mittlerweile ist fast noch ein Jahr vergangen und ich freue mich total auf den dritten Band.

Alan Moore war der Schreiber hinter den in diesen Baenden gesammelten Geschichten. Er hat aber auch Ideen von seinen Mit-Kuenstlern angenommen und ausgearbeitet. Diese waren derer eine ganze Menge ueber die Jahre, aber heute von Interesse ist Stephen R. Bissette, der Penciller besagter sumpfiger Kunstwerke.

Als Autor von Comics schreibt man nicht nur die Geschichte „runter“, sondern man muss sich auch ueberlegen, wie eine Bildkomposition aussehen soll, wie die Panels angeordnet sein sollen, ob die Grenze eines Panels durchbrochen werden soll usw. usf. All dies traegt dazu bei, dass Comics ein viel dynamischeres Medium sein kønnen, als Buecher (und somit „naeher“ an Filmen).
Aber die Umsetzung all dieser Dynamik haengt massiv an den mitschaffenden Kuenstlern neben dem Autor. Und hier ist die Verbindung zu Stephen R. Bissette. Denn das tolle an diesen Swamp Thing Ausgaben ist, dass Alan Moore das nicht nur geschrieben hat, sondern er hat das geschrieben mit den speziellen Talenten der Anderen im Hinterkopf.

Im Nachwort zum ersten Band beschreibt Stephen R. Bissette die Arbeit an Swamp Thing als einen „Tanz“ in dem die teilnehmenden Taenzer (der dritte wird beim naechsten Mal wichtig) aufgingen, weil es fuer sie so natuerlich war diese Kunstwerke jeden Monat zu erschaffen.

Und das sieht und fuehlt man! Man kønnte einzelne Panele oder ganze Seiten dieser Swamp Thing Ausgaben nehmen und ohne Weiteres ins Museum haengen. Und dank der Sammelbaende kann nun auch ich an dieser Kunst teilhaben :)

Ich erwaehnte bereits, dass meine Flottentraeger eine Besatzung braucht um den zu bedienen. Diese Kosten belaufen sich ueber mehrere Monate auf hunderte Millionen Credits. Deswegen, und weil ich trotz angestrengtem Nachdenkens einfach keinen guten Grund fand dieses Spielzeug zu behalten, habe ich mich entschlossen meinen Flottentraeger wieder zu verkaufen. Ich bekomme zwar das meiste Geld zurueck (der war ja noch ganz neu!), aber dieses kurze „Abenteuer“ hat mich ungefaehr 150 Millionen Credits gekostet. Bei einem Kontostand von 5 Milliarden Credits ist das zu verkraften.

Hier nochmal eine letzte Landung …

… und dann war’s das mit mir im Flottentraegerbusiness.