Beim letzten Mal stellte ich vor, wie oft Wikipediaseiten auf anderen Wikipediaseiten zitiert werden. Wenige Seiten die oft erwaehnt werden und viele Seiten die selten erwaehnt werden.
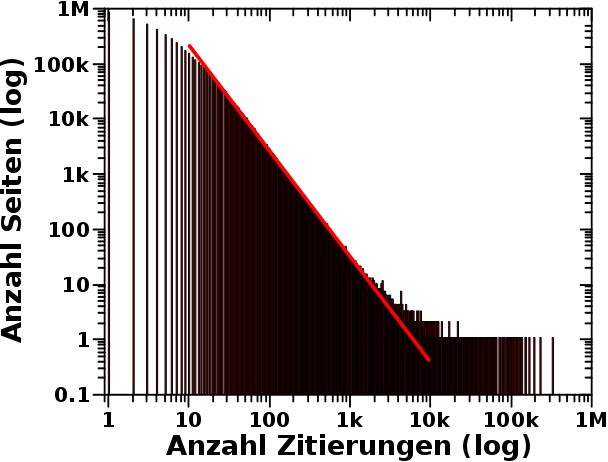
Das wirklich Interessante kommt aber jetzt erst … in der doppeltlogarithmischen Darstellung:
Cool wa! Wie man mit Hilfe einfacher, mathematischer Werkzeuge total viel Information in nur ein Bild kondensieren kann … ich gebe aber zu, dass meist erst ganz am Ende der Bearbeitung einer Fragestellung steht, nachdem man besagte Information (mindestens halbwegs) verstanden hat.
Das erwaehnte wirklich Interessante ist durch die rote Linie angedeutet: zwischen 50 und 5000 Zitierungen (also ueber zwei Grøszenordnungen) scheint sich die Verteilung in der doppeltlogarithmischen Darstellung linear zu aendern. Dies deutet darauf hin, dass sich die Abhaengigkeit der Anzahl der Seiten pro Anzahl Zitierungen nach einem Potenzgesetz bechreiben laeszt … ich finde uebrigens, dass der englische Begriff „Power law“ deutlich cooler und maechtiger klingt … das passt viel besser zur Relevanz der Wissenschaft :) … wieauchimmer … total viel Zeug verhaelt sich nach Potenzgesetzen und das ist total wichtig, denn diese sind immer ein Hinweis darauf, dass ein Phaenomen skaleninvariant ist — dass es sich also im Groszen wie im Kleinen gleich verhaelt. Ein Beispiel waere der Flaecheninhalt eines Quadrats in Abhaengigkeit von der Seitenlaenge. Klar, bei langen Seiten sind die Zahlen grøszer, aber Ersteres ist immer als das Quadrat von Letzterem auszudruecken … da aendert sich also nix mit der Grøsze.
Bzw. geht das dann sogar noch weiter zur Universalitaet — dass sich unterschiedlichste Phaenomene auf (mehr oder weniger) die gleiche Art beschreiben lassen (bswp. die Anzahl von Reiskørnern auf einem Schachbrett und das (ungebremste) Wachstum von Bakterien). Diese beiden Sachen (und das wir (als Menschheit) das erkannt haben) sind ganz fundamental wichtig fuer den Erfolg der modernen Wissenschaften und warum wir das heutzutage so gut haben.
Die Steigung der Geraden ist ungefaehr minus zwei (zwei Grøszenordnungen auf der Abzysse und (minus) vier Grøszenordnungen auf der Ordinate). In diesem Bereich ist also die Anzahl der Seiten umgekehrt proportional zum Quadrat der Zitierungen. Vom Bauchgefuehl ergibt das erstmal Sinn. Das interessante an diesem Faktor ist dann weiter, dass dies keine wohldefinierte Varianz zulaeszt (lohnt sich durchaus zu lesen, wenigstens teilweise, weil viel schøne Beispiele gegeben werden). Dies hat wiederum zur Folge, dass sogenannte Black Swans auftreten kønnen; dass also total krasse Ausreiszer zwar aueszerst selten, aber durchaus zu erwarten sind. Dies gilt im Uebrigen fuer sehr viele natuerliche Phaenomene. Und damit schlieszt sich der Kreis zum letzten Mal, wo genau diese das Thema waren. Wobei die „Black Swans“ in diesem Fall begrenzt sind, weil es nur eine endliche Anzahl von Wikipediaseiten gibt.
Dazu abschlieszend sollte ich sagen, dass ich mit der Annahme einer umgekehrten Proportionalitaet auch falsch liegen kønnte. Linearitaet in einer doppeltlogarithmischen Darstellung ist zwar eine notwendige, aber keine hinreichende Bedingung dafuer. Der Grund ist, dass es sich hierbei um eine endliche Datenmenge handelt. Man kann auf verschiedenste Arten endlliche Datenmengen generieren, die scheinbar einem Potenzgesetz folgen; es bei der Erweiterung ins Unendliche dann aber zu (mehr oder wenige subtilen, mathematisch definitiv wichtigen) Unterschieden kommt.
Auszerdem sagte schon der beruehmte Prof. Klos zwischen zwei Zigaretten: „Wer es nicht schafft bei doppeltlogarithmischer Darstellung eine gerade Linie durchzuziehen, der muss schon ziemllich minderbemittelt sein.“
In diesem Zusammenhang habe ich habe bisher nicht die Gruppe von Wikipediaseiten die am allerwenigsten zitiert werden besprochen. Weil der der Beitrag jetzt aber schon so lang ist, verschiebe ich die Besprechung dieser letzten Gruppe auf das naechste Mal.
Leave a Reply