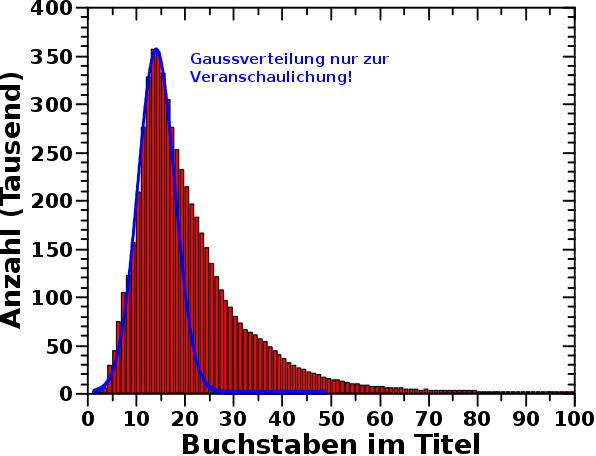
Rekorde bzgl. des laengsten bzw. kuerzesten Titel sind zwar nett, aber die haben wenig Aussagekraft, was man denn prinzipiell erwarten kann. Deswegen schaute ich mir mal die Verteilung der Laenge aller Titel aller Wikipediaseiten an. Diese Verteilung sieht so aus …
… und das ist ganz bestimmt keine Normalverteilung, denn die habe ich zum Vergleich mit eingezeichnet.
So richtig verwundert war ich erstmal nicht, denn ich hatte nix erwartet. Aber dann fragte ich mich doch, warum das keine Normalverteilung ist.
Prinzipiell muss das keine Gaussverteilung sein. Die Geschwindigkeitsverteilung der Konstituenten eines idealen Gases folgen einer Maxwell-Boltzmann-Verteilung. Wie oft die Erde pro Jahr von Meteoriten getroffen wird, die grøszer sind als 1 m folgt einer Poisson-Verteilung. Aber wenn ich nix weiter weisz, dann nehme ich erstmal eine Gaussverteilung an. Das war schon bei meinen vielen Muenzwuerfen und auch bei meinen Untersuchungen der Fibonaccifolge erfolgreich.
Mit dem „dicken“ Teil rechts vom Peak kønnte es eine Maxwell-Boltzmann-Verteilung sein. Ich habe versucht die Daten mit dieser Funktion anzupassen und das funktioniert nicht. Gut so, denn dann haette ich mir Gedanken machen muessen, warum die Verteilung der Anzahl der Buchstaben der Titel der Wikipediaseiten ausgerechnet einer Maxwell-Boltzmann-Verteilung folgt.
Wenn man sich die Verteilung aber nun genau anschaut, dann sieht man zwei „Schultern“. Die eine bei ca. 35 Buchstaben sieht auch das ungeuebte Auge. Die andere um ca. 23 Buchstaben sieht man eigentllich nur, weil die roten Balken nicht der blauen Kurve folgen.
Schultern sind oft ein Zeichen dafuer, dass das Gesamtsignal durch mehrere Prozesse zustande kommt. Ich persønlich kenne das aus der Halbleiterphysik, in der das Gesamtsignal optischer Halbleiter oft aus Rekombinationskanaelen unterschiedlicher Energie (vulgo: unterschiedliche Wellenlaenge) stammt.
Zur besseren Veranschaulichung stelle man sich eine RGB-Leuchtdiode vor. Diese besteht eigentlich aus drei Leuchtdioden, einer roten, einer gruenen und einer blauen, die nahe beineinander sind. Wenn nun alle drei von denen gleichzeitig an sind, nimmt das Auge das Gesamtsignal als weiszes Licht wahr. In dem Fall haben wir also drei Prozesse die unabhaegig voneinander sind und in der Summe etwas sehr anderes ergeben als einzeln betrachtet — naemlich besagtes weiszes Licht anstatt einer wohldefinierten Farbe.
Das Licht welches jede einzelne Leuchtdiode aussendet ist nun aber nicht streng „einfarbig“. Die Leuchtdioden emittieren nicht bei nur einen einzelnen Wellenlaenge sondern das Maximum der Emission liegt auf einem gewissen Wert (den wir dann bspw. als „rot“ sehen) und mit geringerer Wahrscheinlichkeit wird Licht høherer und niedrigerer Wellenlaenge ausgestrahlt. Die Wahrscheinlichkeit welche Wellenlaenge ausgestrahlt wird ist normalverteilt.
Kurzer Abstecher: ein Laser emittiert auf einer einzigen Wellenlaenge … naja, streng genommen emittiert auch ein Laser nicht auf ganz genau auf nur einer einzigen Wellenlaenge, aber fuer die meisten praktischen Betrachtungen ist das nicht so wichtig, denn die „Streuung“ um die Zentralwellenlaenge ist viel geringer als bspw. bei Leuchtdioden.
Lange Rede kurzer Sinn: man kann das weisze Licht einer RGB-Leuchtdiode mittels drei unabhaengigen normalverteilten Prozessen erklaeren.
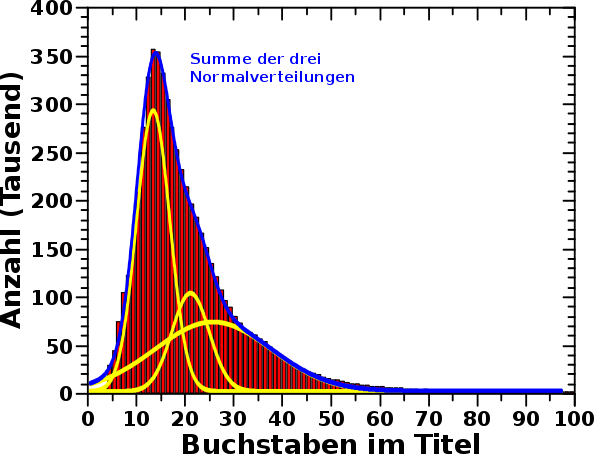
Wenn ich nun die Daten mittels drei Gaussverteilungen anpasse, erhalte ich dieses Bild:
Die blaue Kurve entspricht der Summe der drei unabhaengigen Gaussverteilungen (gelb). Dass die Anpassung so gut ist, deutet darauf hin, dass meine Annahme dreier unabhaengiger (gaussverteilter) Prozesse mglw. richtig ist … andererseits, wenn man genuegend Normalverteilungen nimmt, kann man alles mehr oder weniger gut anpassen.
Die erste unabhaengige Verteilung dominiert den Peak und das Zentrum dieser liegt bei ungefaher 13.23 Buchstaben. Der zweite Prozess ist deutlich schwaecher (die Amplitude der Gaussfunktion ist nur ca. ein drittel so grosz) und das Zentrum liegt bei ca. 21.07 Buchstaben. Der dritte Prozess liegt mit einem Zentrum von ca. 25.81 Buchstaben allerdings ziemlich weit entfernt von den oben erwaehnten ca. 35 Buchstaben. Von der „Staerke“ aehnelt dieser dem zweiten Prozess, ist aber deutlich weniger „definiert“. Die, diesen Prozess beschreibende, Gausskurve ist sehr breit und ueberlappt signifikant die beiden anderen Prozesse.
Das ist natuerlich nicht „die ganze Geschichte“. Wenn die Tittellaenge deutlich mehr als 50 betraegt wird die Verteilung ueberhaupt nicht gut mit diesen drei Prozesen beschrieben. Das ist aber nicht unerwartet und tut relativ wenig zur Sache. Letzteres liegt natuerlich daran, weil es davon insgesamt so wenige gibt und die fallen dann unter das was ich im allerersten Satz bereits schrieb.
Nun ist natuerlich die Frage, was diese drei Prozesse sein kønnten?
Ehrlich gesagt, habe ich ueberhaupt keine Idee, was der dritte Prozess ist. Aber bei so einer breiten Gausskurve kønnte da alles møglich mit dazu zaehlen. Bei den ersten beiden Prozessen habe ich aber eine Vermutung: die englische Sprache an sich und Namen. Dazu mehr beim naechsten Mal.
Leave a Reply