Ich besuchte Nyauthai AA-A h0 A. Dies ist einer der seltenen und kurzlebigen B (Blue-White super giant) Stars. Aehnliche Sterne in dieser Kategorie die vom Ursprungssytem aus gesehen werden kønnen sind bswp. Rigel oder Deneb. Aber ich besuchte Nyauthai AA-A h0 A, denn dieser war nahe an der Position wo ich mich befand und er haelt gleich zwei Rekorde.
Der erste Rekord ist leicht zu verstehen: der Wert der groszen Halbachse des Orbits dieses Sterns. Dieser betraegt 51,478,664,314,880.0 m oder ca. 344.11 astronomische Einheiten (fast neun mal laenger als die grosze Halbachse des Zwergplaneten Pluto im Urpsrungssytem!). Das ist der grøszte Wert fuer alle bisher bekannten B (Blue-White super giant) Stars und dieser Wert faellt direkt aus den Daten des groszen galaktischen Atlas heraus.
Spannender hingegen ist der naechste Rekord — der Umfang des Orbits — denn dieser muss berechnet werden.
Eine Abschaetzung waere einen kreisførmigen Orbit anzunehmen. In diesem Fall (und ueberhaupt in den allermeisten Faellen) wuerde diese Abschaetzung einen Wert ergeben, der gar nicht mal so schlecht ist. Dies liegt daran, weil die Exzentrizitaet \(\varepsilon\) des Orbits dieses Sterns beinahe Null und der Orbit somit (fast) gar nicht gestreckt ist.
Andererseits mache ich diese Berechnung fuer ALLE bekannten Himmelskørper. Und bei ueber 100 Millionen (gemeldeten) Sternen und Planeten sind etliche dabei, bei denen diese Abschaetzung unakzeptable Werte liefern wuerde.
Deswegen entschied ich mich den Wert jedes Mal komplett zu berechnen … also nicht ich persønlich und manuell … vielmehr macht das natuerlich das Programm welches ich zur Auswertung der Daten schrieb automatisch.
Eine exakte Løsung dieses Problems existiert. Leider handelt es sich dabei um ein Integral ohne analytische Løsung. Das haette ich zwar approximieren kønnen, aber bei hunderten von Millionen von Berechnungen wuerde das eine nicht akzeptable Verlangsamung des Rekordsuchprozesses bedeuten … das Programm braucht bereits so schon deutlich mehr als fuenf Stunden.
Gluecklicherweise hat Srinivasa Ramanujan vor ueber 1000 Jahren (genauer gesagt im Jahre 1914) im Quarterly Journal of Mathematics, XLV, p. 350 — 372, einen Artikel mit dem Titel „Modular equations and approximations to π“ verøffentlicht. Dort findet sich in Paragraph 16 eine Formel, mit der man den Umfang einer Ellipse ziemlich gut annaehern kann:
Es gilt
wobei \(a\) die grosze und \(b\) die kleine Halbachse des Orbits ist. Der Wert fuer letztere findet sich leider nicht in den Rohdaten. Hingegen findet man dort \(\varepsilon\) und damit ist \(b\) bestimmt durch:
Damit erhaelt man einen Wert von ca. 32.3 Tm fuer den Umfang des Orbits dieses Sterns. Das ist der grøszte Wert fuer alle Sterne in dieser Kategorie.
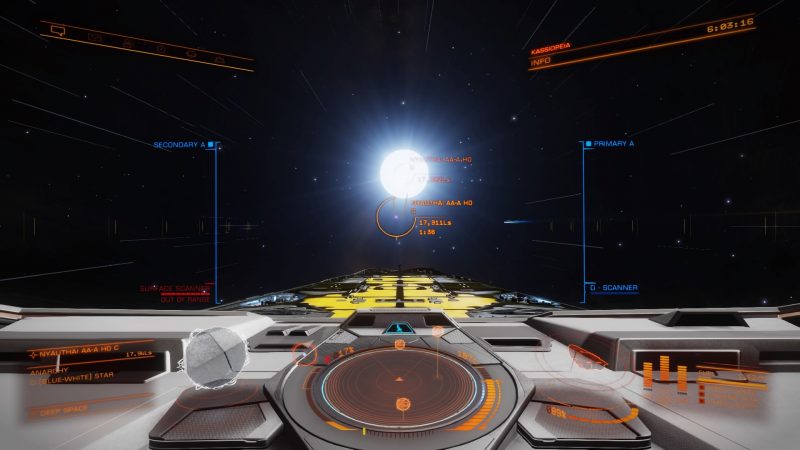
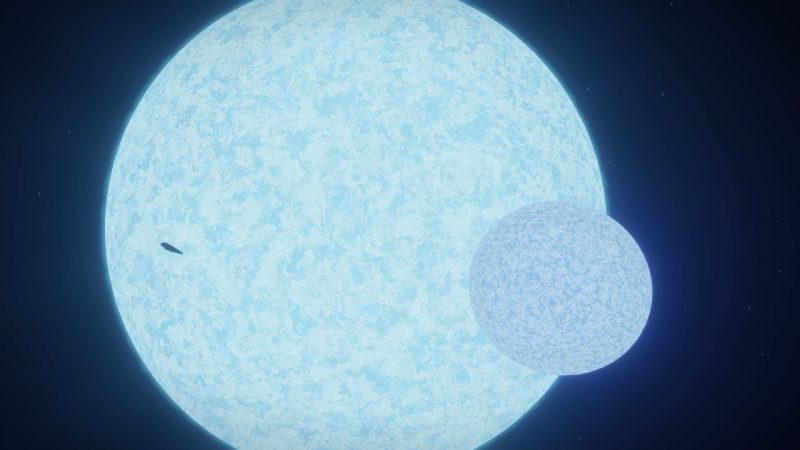
Ich bin da also hingeflogen und O! M! F! G! … Super giants sind tatsaechlich RIESIG! Here bin ich mehr als siebzehntausend Lichtsekunden vom Stern weg!. Zum Grøszenvergleich waehlte ich den Begleiter des Rekordhalters an (ja, das ist der Punkt im orangen Dreiviertelkreis). Der ist nur nicht „klein“ … der ist acht mal grøszer als Sol!
Und genaus das ist einer der Gruende, warum ich mich fuer diese Reise entschied.
Ich flog dann bis auf 111 Lichtsekunden an den Begleiter heran (der eigentliche Stern von Interesse ist noch deutlich weiter weg).
Das sieht jetzt alles gar nicht so grosz aus, aber das haengt natuerlich an der Perspektive.
Normalerweise wuerde ich zwischen den beiden Sternen hindurch fliegen. Aber dieses mal war ich ueberhaupt nicht versucht dies zu tun. Denn die sind beide sehr sehr warm. Wenn ich das naechste Mal Zugriff auf Kuehlkørper habe, werde ich wohl einen installieren. Fuer genau solche Situationen, und das obwohl ich dadurch ein bisschen Sprungreichweite einbueszen werde.
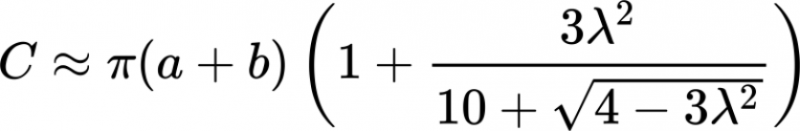
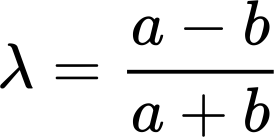
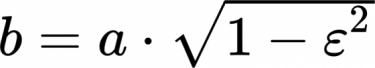
Leave a Reply