Søren in Norwegen

… habe ich diesen Artikel, weil ich dachte, dass der von Dietmar waere.

Aber darin steht etwas, was mich darin bestaetigt auch weiterhin ueber die „protestantisch, kapitalistische Arbeitsmoral“ zu schimpfen.

Und nein, dass ist NICHT strikt im Sinne Max Webers gemeint. Bei Interesse kann ich das ja mal naeher erlaeutern.

Jedenfalls steht in dem Artikel:

[Luther gab] [a]llgemein geläufigen Begriffen hingegen […] einen neuen Sinn; „Arbeit“ bedeutet bei ihm nicht mehr nur Qual und Mühe, sondern – erheblich positiver – die Gestaltung der Welt.“

Denn wer mag sich (insbesondere heutzutage und im sozialen Habitat sog. Akademiker) schon eingestehen, dass sie oder er sich mit was rumquaelt und das eigentlich gar nicht machen will, weil coolere Sachen warten?

Wieauchimmer, ich halte mich mehr an die urspruengliche Bedeutung des Wortes „Arbeit“ und freue mich auf die Roboter :) .

… als ich.

Einen wichtigen Teil ueber den ich ich mich hier lang und breit ausliesz, fasst Noam Chomsky kurz zusammen:

…if you ask me whether or not I’m an atheist, I wouldn’t even answer. I would first want an explanation of what it is that I’m supposed not to believe in, and I’ve never seen an explanation.

H. L. Menken (den ich hier bereits indirekt zitierte), hat viele Dinge gesagt, darunter auch so Einiges, was unter heutigen Gesichtspunkten zu beanstanden waere. Aber er sagte mindestens eine wichtige Sache, die ich hier gerne wiedergeben møchte, spiegelt sie doch meine (nicht alltaegliche, aber oft genug und immer wiederkehrende) Lebenserfahrung wieder:

The trouble with fighting for human freedom is that one spends most of one’s time defending scoundrels. For it is against scoundrels that oppressive laws are first aimed, and oppression must be stopped at the beginning if it is to be stopped at all.

… war ja bekanntermaszen mal ’n Baby. Da fragte ich mich neulich, ob er sich waehrend seiner Pubertaet auch mit seinen Eltern gestritten hat und ob er aus Trotz und jugendlicher Rebellion wegen mal ’ne Weile Atheist oder (starker … tihihihi) Agnostiker war.  Wobei ich ja Letzteres witziger faende. Als Atheist lehnt man ja nur die „Beweise“ fuer Gott ab; Atheisten muessten, wenn sie konsequent waeren, nach eigener Logik einen Gott anerkennen, wenn die Beweise dafuer stark genug waeren. Das ist auch (der hauptsaechliche Grund, warum ich kein Atheist bin). Waehrend man als (starker) Agnostiker eine „Gotteserfahrung“ grundsaetzlich nicht anerkennt. … Tihihihi … ein jugendlicher Jesus, der jeden Tag mit seinem Vater spricht und dann eine Gotteserfahrung nicht anerkennt … jup … hørt sich an wie Pubertaet … Tihihihi.

Diese Idee wurde mir gegeben vom jungen Mann, der bei mir wohnt … also nicht das mit dem Agnostiker, aber dass Jesus ja auch mal in der Pubertaet gewesen sein muss.

Wenige Wochen spaeter stellte sich heraus, Walter Moers diese Idee bereits in „Jesus total“ umsetzte. Ueberhaupt ist dieses Buch absolut empfehlenswert fuer 10-jaehrige! Und mindestens genauso wertvoll fuer die praepubertaere Entwicklung sind meiner Meinung auch die „Adolf – Ich bin wieder da“ Geschichten vom selben Autor.

Und da ich gerade dabei bin, aber mir nicht so richtig einfaellt, wie ich das in einen eigenen Eintrag packen kønnte, møchte ich an dieser Stelle auf den Artikel „Statistical inquiries into the efficacy of prayer“ von Francis Galton im Fortnightly Review vol. 12, Seiten. 125-35, 1872 hinweisen (hier ein Nachdruck in einem modernen Journal). Galton praesentiert dort seine wissenschaftlichen Untersuchungen und Ueberlegungen bzgl. der Wirksamkeit von Gebeten und ich dachte mir, dass das euch, meine lieben Leserinnen und Leser mglw. interessieren kønnte.

Wie bereits mehrfach erwaehnt, schau ich am Ende eines Programmierprojects immer nochmal drueber und schreibe Kommentare.

Irgendwie witzig ist dann, wenn aus einem …

ATTENTION: The following line of code is important otherwise the program will stop to function

… ein …

The following line of code is probably not neceassary

… wird, weil man in der Zwischenzeit was Neues gelernt hat.

Ich war dann aber zu faul das genauer zu untersuchen, denn ich aendere den Code eines funktionierenden Programs nur sehr widerwillig und nur, wenn es wirklich sein muss oder ich genuegend Zeit habe, die Konsequenzen zu uebersehen.

Eigentlich ist das Thema „Fair Coin“ soweit abgeschlossen, da alle Fragen beantwortet sind, aber eine Sache liegt mir noch am Herzen.

Ich habe ueber 35.000 Dateien erschaffen im Zuge dieser Experimente. Die Allermeisten davon erschuf natuerlich nicht ich persønlich manuell, sondern meine Programme automatisch. Inwiefern _ich_ dann als Schøpfer gesehen werden kønnte, waere an und fuer sich schon ’ne Diskussion wert, obgleich diese eher akademischen Charakter haette. Aber ich schwoffte ab.

Diesen Datenreichtum (tihihihi) habe ich euch, meinen lieben Leserinnen und Lesern, aber nicht gezeigt. Ihr habt nur schicke bunte Bilder zu sehen bekommen. Ihr kønntet also die hier praesentierten Erkenntnisse nicht nachpruefen, so ihr denn wolltet.

Und dies ist meiner Meinung nach falsch. Damit mache ich mich zum Herrscher ueber die Rohdaten und nur wer mich kennt und danach fragt, kønnte damit arbeiten.

Dies ist die traditionelle und (leider immer noch) uebliche Herangehensweise in der Wissenschaft und meiner Meinung nach enthaelt diese Herangehensweise die implizite Annahme, dass der Herrscher ueber die Daten schon am Besten weisz, was damit anzufangen sei und sowieso schon alles rausgefunden hat.

Nun ja … meine Meinung bzgl. Herrschern sollte hinreichend bekannt sein.

Deswegen befreie ich diese Rohdaten und die Programme zu deren Erschaffung.

Alles ist bei Zenodo hochgeladen.

Haeh? WHUT? Nun fragt ihr euch sicher, warum ausgerechnet ICH mein Zeug in die Cloud auf anderer Leute Computer lade?

Meiner Meinung nach ist das alles knorke dieses Mal und wer verstehen møchte, warum ich (in diesem Falle) diesen Service benutze, der mag hier lesen.

Die Daten wurden unter einer Creative Commons Attribution-ShareAlike 4.0 Lizenz verøffentlicht.
Die Programme (selbstverstaendlich) unter der GNU General Public License Version 3.

Und wo genau findet ihr nun die Daten?

Ganz einfach, unter dem DOI (oder _der_ DOI? … Ich bin da unsicher): 10.5281/zenodo.546671.

Und damit schliesze ich diese Miniserie ab.

Im weitestens Sinne kann man Roboter und kuenstliche „Intelligenz“ verstehen, als Nicht-Menschen, welche mehr und mehr vormals von Menschen erbrachte Leistungen uebernehmen.
Darunter fallen auch elektronischen Reklametafeln:

Kein Mensch muss fuer diese Papier, Farbe oder Leim herstellen. Kein Mensch muss diese Reklame mehr drucken, verteilen oder wieder abnehmen. Die Kapitalisten schicken das, fuer was sie Reklame haben wollen, nur noch an an einen Computer der diese Tafeln steuert. Eine kuenstliche „Intelligenz“ sorgt dann dafuer, dass diese „Information“ verteilt wird.
Heutzutage brauchen wir natuerlich noch Menschen, die diese Tafeln installieren, aber das war ja nicht anders bei den Plakattafeln frueher.

Aber warum sage ich, dass das gut ist?

Zum einen natuerlich, weil die Herstellung von Farbe, Leim und Papier und das tonnenweise Herumfahren von Selbigem nicht gerade als umweltfreundlich angesehen werden kann.

Zum anderen aber, weil die alte Form der Werbung mit Papierplakaten scheinbar (mglw. anscheinend?) unsexy geworden ist fuer Kapitalisten. Na klar, da blinkt und bewegt sich ja nichts.

Aber die alten Werbetafeln sind noch vorhanden und der leere Platz fuehrt dann erstmal zu Werbung fuer Werbung:

Und nach einer Weile richtet wohl eine „unsichtbare Hand“ den sogenannten „Markt“ und ich nehme an, dass Werbung auf diesen alten Flaechen deutlich billiger wird und pløtzlich andere Interessen als „Geld verdienen“ dort angepriesen werden kønnen:

Das finde ich toll! Da will ich mehr von haben!

Danke Roboter!

Wenn ein Mann, auf die Frage, was man denn heute Abend machen will, zu seiner Freundin/Frau sagt „du kønntest mir den ganzen Abend lang einen blasen“, so wird das (hoffe ich) i.A. als „nicht in Ordnung!“ (mit Ausrufezeichen!) betrachtet. Und irgendwie meiner Meinung nach auch durchaus zu Recht.

Aber wenn eine Frau das Gleiche sagt, so wird es pløtzlich irgendwie als „Frauenpower“ angesehen. Aufgrund der (immer noch!) bestehenden systematischen Unterdrueckungsmechanismen mein ich auch hier: durchaus zu Recht.

Andererseits fuehlt sich das auch ein bisschen an, als ob hier mit zweierlei Masz gemessen wird.

Ich møchte nicht, dass das falsch verstanden wird!

Ich denke absolut NICHT, dass Frauen zu viel duerfen und wir, „die armen armen Maenner“, benachteiligt sind.

Aber wie ich bereits hier und hier schrieb, løst die Errichtung eines Matriarchats auch nicht das eigentliche Problem!

Und zum Abschluss wieder eine Erinnerung bzgl. der oben angesprochenen, real existierenden systematischen Unterdrueckungsmechanismen:

… muessen den Zeitpfeil selbstverstaendlich nicht beachten:

Wien ist uebrigens wirklich eine Reise wert … oder zwei … oder drei (ich werde da ganz bestimmt noch ein drittes Mal hinfahren).

Die haben dort naemlich die Venus von Willendorf. Deren Existenz ist seit meiner Kindheit und den Dinosaurierbuechern, welche auch immer irgendwie gleich noch die Steinzeit mit abgehandelt haben, und mglw. auch durch die Schule, so fest verankert in meinem Unterbewusstsein, dass das irgendwie krass, cool, erstaunlich, beeindruckend, wasweiszichaufjedenfallherausragend war, die in Echt zu sehen.

Und im Museum gegenueber haengt da mal einfach so „Die Kreuztragung Christi“ von Pieter Bruegel dem Aelteren! Da bin ich ja aus allen Wolken gefallen, als ich das nichts ahnend auf meiner Entdeckungsreise pløtzlich … aehm … nun ja, eben entdeckte.

Und auszerdem schaeme ich mich sehr, dass ich noch nie so richtig was von Egon Schiele gehørt hatte. Also gehørt hatte ich den Namen schon mal, aber ich konnte den nicht nur nicht einordnen, sondern sein Schaffen ging vøllig an mir vorbei bisher. Eine Schande! Und meiner Meinung auch ein Versagen unseres Bildungssytems. Gustav Klimt konnte ich ja wenigstens so ganz grob einordnen, aber dass ich als dtsch.-sprachiger (und erzogener), intelligenter und (ich denke doch) halbwegs gebildeter Buerger nix von Egon Schiele wusste ist … mhm … jetzt wo ich einige seiner Werke gesehen habe wuerde ich sagen kommt dieser Umstand ziemlich nah an die Kategorie „unverzeihlich“.
Jedenfalls diese Bildungsluecke diesen unbekannten Bildungs-Grand-Canyon konnte ich in Wien endlich schlieszen.

Und auch Beethoven ist dort begraben.
Ueberhaupt ist der Wiener Zentralfriedhof durchaus einen Besuch wert. Insb. die alten juedischen Graeber sind beachtenswert.

Das einzige was mir nicht so gefaellt ist das Anklammern an alles was die Monarchie betrifft … aber naja … das haengt wohl mit meiner eigenen Weltanschauung und (nicht nur) politisch, gesellschaftlichen Ansichten zusammen.

In den vorhergehenden Beitraegen in dieser Reihe habe ich im Wesentlichen ueber Ketten von ein und demselben Resultat eines Muenzwurfes geschrieben.

Ist ja auch aeuszerst spannend, denn so intuitiv weisz man ja, dass Kopf oder Zahl nicht viel øfter als drei oder vier mal hintereinander kommen sollte.

Aber wie ausfuehrlich untersucht taeuscht diese Intuition gewaltig, selbst innerhalb von Versuchsparametern, welche praktisch durchfuehrbar sind. Bspw. als Mathelehrer oder fuer ein Kasino.

Diese Kopf- oder Zahlketten waren eine intellektuelle Herausforderung, und somit ein Quell groszer Freude, fuer mich. Deswegen habe ich es hier so ausfuerhlich behandelt, weil ich euch, meine lieben Leserinnen und Leser, gerne an meiner Freude teilhaben lassen wollte. Aber der urspruengliche Ausløser meiner Ueberlegungen zu diesem Thema war etwas ganz anderes.

Wie ich im ersten Artikel dieser Miniserie schrieb, interessierte ich mich urspruenglich dafuer, wie viel øfter ich bspw. Kopf werfe, wenn ich eine Muenze so und so oft werfe.
Es interessierte mich also eigentlich der „Ueberschuss“. Oder anders: Hat eine faire Muenze eine „natuerliche Tendenz“ ein Ungleichgewicht auszugleichen.

Wiederum rein intuitiv fuehlt man, dass dem so ist. Allein schon der Ausdruck „faire Muenze“ traegt viel dazu bei.

Wie es nun aber wirklich aussieht behandle ich in diesem Beitrag.

Zur Erinnerung: ich machte (im Wesentlichen) jeweils 1000 Experimente mit jeweils 10, 100, 1.000, usw. fairen Muenzwuerfen pro Experiment. Diese Experimente wiederholte ich, mit einer unfairen Muenze.

Nun schaute ich am Ende jedes Experiments, wie viel øfter Kopf bzw. Zahl geworfen wurde.

Am Beispiel der 1000 Experimente mit jeweils 10 Wuerfen pro Experiment ist dies dargestellt, im linken Bild dieser Abbildung:

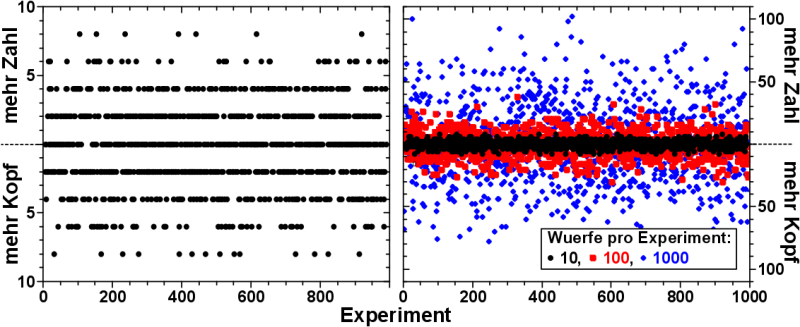
Auf den ersten Blick (und auch wenn man das naeher untersucht) ist der Durchschnittswert fuer den „Ueberschuss“ eines Resultats gleich Null. Das Wesensmerkmal einer fairen Muenze eben.

Im Fall der 10 Wuerfe pro Experiment kann natuerlich Kopf nicht haeufiger als „10 mal øfter als Zahl“ auftreten und umgekehrt.
Fuehre ich mehr Wuerfe pro Experiment durch, erhøht sich diese Grenze und es werden høhere „Ueberschuesse“ erreicht, aber der Durchschnittswert fuer den „Ueberschuss“ bleibt gleich.
Dies ist im rechten Bild der Abbildung dargestellt.

Schauen wir uns etwas naeher an, wie die Ueberschussverteilung aussieht, fuer die 1000 Experimente mit jeweils 10 Millionen Wuerfen pro Experiment:

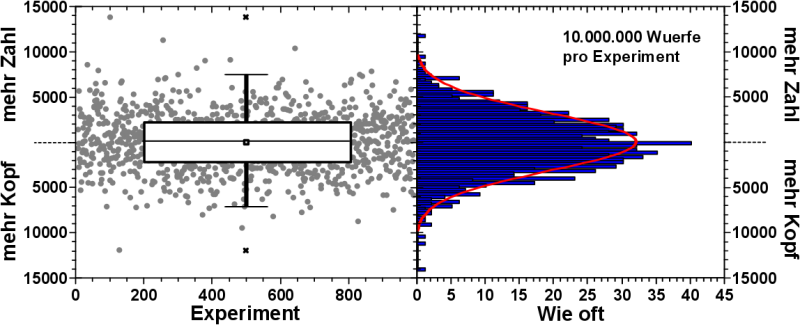
Im linken Bild legte ich ueber die (grauen) Punkte, welche wiederum den Ueberschuss eines Reslutats pro Experiment darstellen, einen Boxplot. Das kleine Viereck innerhalb der Box ist der Mittelwert und dieser ist leicht verschoben gegenueber der Nullinie mit einem Wert von 65. Alle anderen Werte betrachtend, kann dies weiterhin getrost als „auf der Nulllinie liegend“ angesehen werden.

Innerhalb der Box befinden sich 50 % aller Ueberschusswerte. Die gleiche Ausdehnung der Box, sowohl nach Oben als auch nach Unten (von der Nulllinie gesehen), ist wiederum Ausdruck der „Fairness“ der Muenze.

Innerhalb der Antennen befinden sich 98 % aller Ueberschusswerte und die extremsten Ausreiszer sind durch die Kreuze gekennzeichnet.

Wie schon bei der Fibonaccifolge, erstellte ich ein Histogramm der Ueberschusswerte und passte dieses mittels einer Normalverteilung an. Da dieses Bild im Wesentlichen die gleiche Information (nur detaillierter) enthaelt wie der Boxplot, gehe ich nicht weiter darauf ein. Ich zeige das hier eigentlich nur, weil ich so grosze Freude daran hatte, das Histogramm zu erstellen und anzupassen und die erwaehnten Erkenntnisse aus dem Boxplot mittels einer anderen Methode bestaetigt zu sehen. Und auszerdem sieht es schick aus; in mehrfacher Hinsicht.

Nun das Gleiche zur unfairen Muenze.

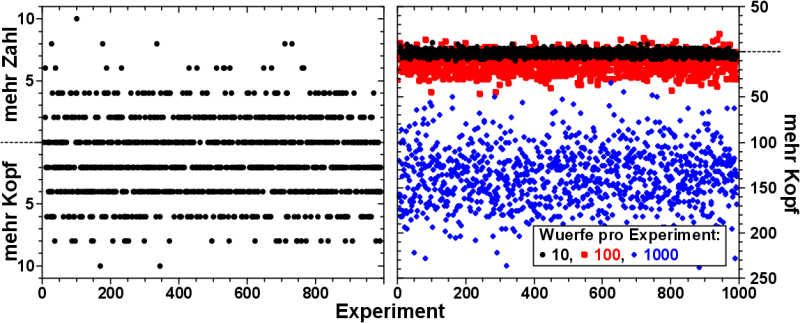
Wie im linken Bild zu sehen, unterscheidet sich der „Ueberschuss“ bei einer kleinen Anzahl Wuerfe pro Experiment (wieder 10 im linken Bild) nicht wesentlich von der fairen Muenze. Wenn man genauer Hinschaut, so kønnte man eine leichte Verschiebung zu einem absoluten Kopf-Ueberschuss vermuten.

Diese Vermutung wird bestaetigt, wenn man diese Untersuchung fuer Experimente mit mehr Wuerfen pro Experiment gegeneinander auftraegt, wie im rechten Bild der Abbildung geschehen.

Wie zu erwarten bildet sich ein absoluter Ueberschuss an Kopf-Wuerfen heraus und dieser Ueberschuss wird grøszer, je mehr Wuerfe pro Experiment stattfinden.

Wird die Verteilung um den Mittelwert betrachtet, so erhaelt man die gleiche Gaussverteilung wie oben am Beispiel der fairen Muenze bereits gezeigt. Im ersten Moment mag dies verwirren, aber die Unfairness dieser Muenze steckt in der absoluten Verschiebung. Wie sehr es im den Mittelwert streut, unterliegt den „regulaeren“ statistischen Gesetzen.

Ich halte somit fest, dass ueber viele Experimente gesehen, beim Wurf einer fairen Muenze im Mittel genau so oft Kopf wie Zahl erscheint. Bei einer unfairen Muenze hingegen (deutlich) øfter Kopf, abhaengig von der Anzahl der Wuerfe.

Toll wa! Das Dumme ist nur, dass man im Kasino nicht ganz viele Experimente macht, sondern nur eins. Und auch wenn es unwahrscheinlich ist, so kønnte rein statistisch gesehen, dies ausgerechnet jenes Experiment sein, welches einen extremen Ueberschuss produziert. Bei einer fairen Muenze ist es dann eine 50/50 Chance dass man auf das richtige Resultat setzt.

Deswegen schaute ich mir mal an, wie sich der maximale Ueberschusswert (bei jeweils 1000 Experimenten) entwickelt, in Abhaengigkeit von der Anzahl der Wuerfe pro Experiment:

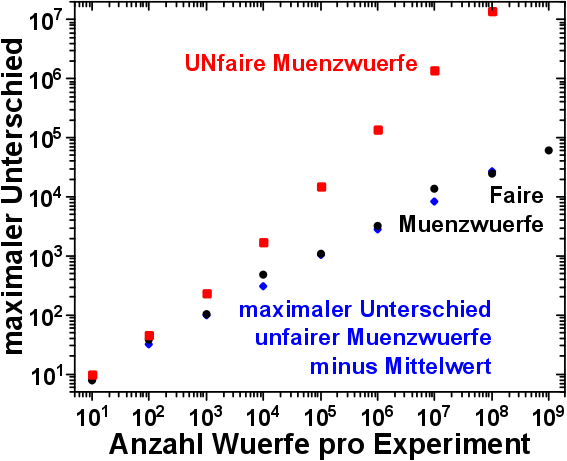
Bei der fairen Muenze (schwarze Punkte) kønnen die etremsten Werte entweder durch einen Zahl- oder durch einen Kopfueberschuss zustande kommen. Dies wird hier nicht unterschieden.

Die Entwicklung des extremsten Ueberschusswertes ist in doppeltlogarithmischer Darstellung linear.

Linearitaet in doppeltlogarithmische Darstellung bedeutet, dass der Anstieg des Wertes des Extremwertes extrem langsam vonstatten geht. Als ob sich das Universum gegen extreme Ungleichgewichte straeubt.

Fuer den absoluten Wert des extremsten Ueberschusswertes bei den unfairen Muenzwuerfen (rote Vierecke) gilt dies natuerlich nicht derart allgemein. Zunaechst einmal ist zu wiederholen, dass es sich hierbei nur um Kopfueberschuesse handelt (mglw. abgesehen von Experimenten mit nur 10 Wuerfen pro Experiment).
Die insgesamt høheren Werten kommen natuerlich durch die absoluten Verschiebung der Ueberschusswerte zustande.
Wird der Mittelwert der absoluten Verschiebung hingegen von den Werten des extremsten Ueberschusswerte abgezogen (blaue Diamanten), so zeigt sich das gleiche Bild wie bei der fairen Muenze.

Wenn man sich die Werte der extremen Ueberschusswerte anschaut, so sind diese aber mitnichten klein. In den von mir durchgefuehrten Experimenten, fiel ein Resultat auch mal mehr als 60.000 mal øfter als das andere Resultat. Zugegeben, das war bei den Experimenten mit 1 Milliarde Wuerfe pro Experiment.

Dennoch, die Lektion aus dieser kleinen Uebung ist die Folgende: Wenn ich gewinnen will, sollte ich schummeln. Denn sowas wie Glueck gibt es nicht. „Pech“ hingegen schon. Das ist naemlich wissenschaftlich ausgedrueckt: „Unwahrscheinlichkeit“ und die katastrofalen Folgen von Unwahrscheinlichkeit zeigte ich in diesem Beitrag.