Søren in Norwegen

Wie in den letzten Beitraegen immer wieder geschrieben, ist es statistisch møglich, dass eine faire Muenze zu ungewuenschten Resultaten fuehrt.

Was man also braucht, ist eine unfaire Muenze, von der wir wissen, wie sie sich verhaelt, aber ohne, dass es auffaellt.
Die Muenze darf also nicht all zu sehr vom normalen Verhalten abweichen.

Etwas mathematischer ausgedrueckt, haette ich also gern eine andere Wahrscheinlichkeitsverteilung.

Als Erstes dachte ich da an eine Poisson-Verteilung. Und auch wenn ich das weiter unten Aufgefuehrte auch alles damit bestaetigen konnte, so ist diese unter gewissen Umstaenden allerdings zu auffaellig bzw. in anderen Faellen unnuetz, da sie sich zu wenig von einer Normalverteilung unterscheidet.

Und dann erinnerte ich mich an eines der schønsten Erlebnisse meiner Studienzeit: wie ich in der Thermodynamik mit der Maxwell-Boltzmann-Verteilung bekannt wurde.

Aber bevor ich ins Schwaermen gerate, stelle ich sie lieber vor:

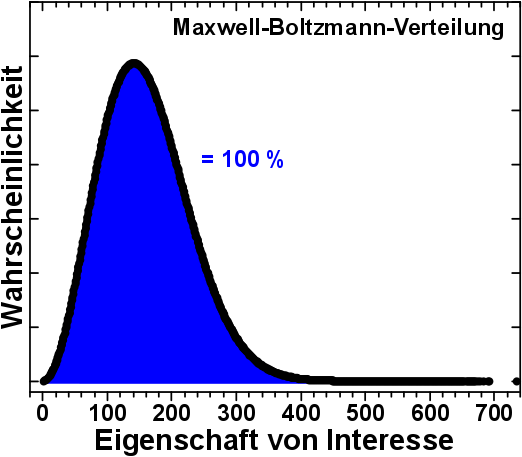
Wie immer wird die Wahrscheinlichkeit, dass eine Eigenschaft von Interesse (bspw. die Geschwindigkeit der Atome/Molekuele eines Gases) einen bestimmten Wert hat aufgetragen.
Die Summe aller Wahrscheinlichkeiten (die Flaeche unter der Kurve) ist gleich 100 %.
Es gibt keine Werte kleiner Null und die Maxwell-Boltzmann-Verteilung hat einen langen „Schwanz“ zu groszen Werten der Eigenschaft von Interesse, mit allerdings sehr kleinen Wahrscheinlichkeiten.

Abgesehen von dem letzten Punkt, scheint die Maxwell-Boltzmann-Verteilung auf den ersten Blick der Normalverteilung sehr zu aehneln. Eine Tatsache, die ja durchaus gewuenscht ist.
Aber um sicher zu gehen, dass die Aehnlichkeit nicht zu grosz ist, schauen wir uns diese Verteilung mal etwas naeher an:

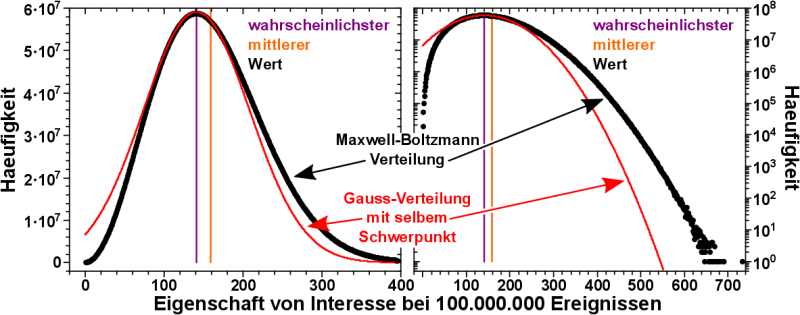
Dies ist die selbe Kurve wie im ersten Bild, aber diesmal mit Zahlen. Es ist die Haeufigkeit einer Eigenschaft von Interesse bei 100.000.000 Ereignissen aufgetragen. Man kønnte sich bspw. die Geschwindigkeit von 100.000.000 Gasmolekuelen denken.

Im linken Bild ist die Haeufigkeit linear abgetragen, im rechten Bild logarithmisch. Man beachte, dass die Ordinatenachse im linke Bild nur bis 400 reicht. Der Grund dafuer ist der im ersten Bild zu sehende „Schwanz“, der wenig (visuelle) Information liefert bei linearer Abszisse.

Die rote Kurve ist eine Gausskurve mit dem gleichen Schwerpunkt (dem wahrscheinlichsten Wert der Eigenschaft von Interessen fuer ein Ereigniss) und angpasster Standardabweichung.

Das meiner Meinung nach Interessanteste an der Maxwell-Boltzmann-Verteilung ist, dass der Mittelwert der Eigenschaft von Interesse fuer alle Ereignisse NICHT mit dem wahrscheinlichsten Wert uebereinstimmt.
Man stelle sich ein Person vor, die nicht schwimmen kann, welche einen See ueberqueren muss, dessen Bodenprofil derart ist, dass die Tiefe aller Punkte mittels einer Maxwell-Boltzmann-Statistik beschrieben werden kann. Nun ja, im Mittel ertrinkt diese Person, aber am wahrscheinlichsten ist, dass sie (oder er) ueberlebt.

Verrueckt wa! eine coole Verteilung eben.

Ein Vergleich der Kurven zeigt, dass Ereignisse mit der Eigenschaft von Interesse linksseitig des wahrscheinlichsten Wertes seltener auftreten als bei einer Normalverteilung; rechtsseitig hingegen haeufiger. Dies gilt auch, wenn man den Schwerpunkt der Normalverteilung auf den wahrscheinlichsten Wert legen wuerde.

Legt man nun fest, dass Werte der Eigenschaft von Interesse kleiner oder gleich als der wahrscheinlichste Wert als „Zahl“ zu interpretieren sind und alle anderen als „Kopf“, hat man eine unfaire Muenze.

Ich liesz meinen Rechner wieder eine Weile rechnen um genuegend „Muenzwuerfe“ beisammen zu haben.

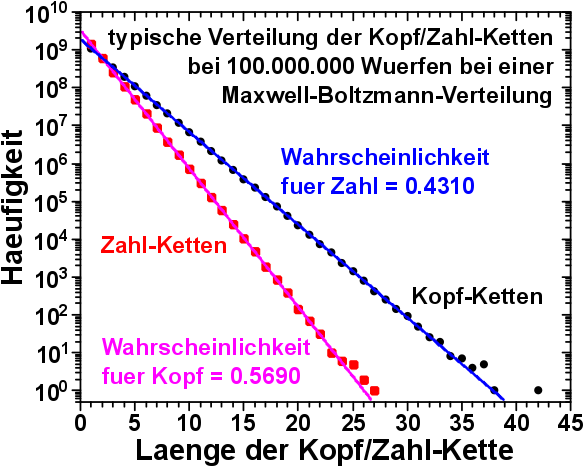
Damit es nicht langweilig wird, komme ich gleich zu den Kopf- und Zahl-Kettenverteilungen und deren Anstieg bei vielen (unfairen) Muenzwuerfen.

Jippie! Diese Muenze ist tatsaechlich unfair! Die Wahrscheinlichkeit eine lange Kopf-Kette zu erhalten ist bei laengeren Kopf-Ketten mehrere Grøszenordnungen høher als die fuer eine Zahl-Kette der gleichen Laenge.

Im Anstieg dieser Kurven, welcher hier noch urspruenglich als „Zerfallskonstante“ falsch interpretiert wurde, steckt also wie vermutet tatsaechlich die Verteilung drin. Mathematisch stellte ich das zwar schon beim letzten Mal dar, aber ’s ist doch schøn auch „in Echt“ zu sehen.