Søren in Norwegen

Es steht die Frage im Raum, wie oft ich bspw. 3 mal hintereinander Kopf (oder Zahl) werfe, wenn ich eine Muenze 100 Mal werfe.

Hintergrund dieser Frage ist immer noch, wie schnell ich pleite gehe, wenn ich all mein Geld auf das jeweils andere Resultat setze und bei jedem Kopf-Wurf meinen Einsatz verdopple.

Und natuerlich interessieren mich nicht nur Ketten von 3-mal-Kopf-(oder-Zahl)-hintereinander, sondern auch alle anderen møglichen Kopf-(oder Zahl)-Ketten.

Und damit ich mir das „(oder Zahl)“ im Weiteren sparen kann, konzentriere ich mich ab sofort im Wesentlichen nur noch auf die „Kopf“-Wuerfe.
Man kann sich ja denken, dass die Kopf-Zahl-Situation mehr oder weniger symmetrisch ist. Innerhalb statistischer Schwankungen, ist das auch erstmal richtig. Mehr dazu in einem viel spaeteren Beitrag.

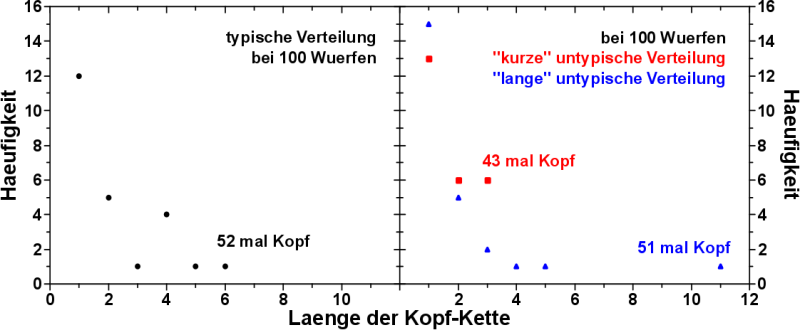
Bei 100 Wuerfen sieht eine typische Kopf-Kettenverteilung so aus wie der linke Graph in diesem Bild:

So einige Male folgte auf Kopf gleich eine Zahl, ein paar Mal folgt auf einen Kopf Wurf gleich noch einer. Høhere Kopf-Ketten treten zwar auf, aber selten.

Zwei untypische (aber innerhalb statistischer Schwankungen durchaus erlaubte) Kopf-Kettenverteilung kann man im rechten Graph sehen.

Bei einer von mir als „kurz“ bezeichneten untypischen Kopf-Kettenverteilung treten keine høheren Kopf-Ketten auf, waehrend bei einer „langen“ untypischen Kopf-Kettenverteilung ein unwahrscheinlich „hohes“ Ereigniss auftritt. In diesem Fall wurde bei letzterem 11 mal hintereinander Kopf geworfen … oioioi … 2¹¹, je nach Ausgangseinsatz ist das schon ’ne ganze Menge Zaster.

Aber das ist natuerlich noch keine Antwort auf die Frage. 100 Wuerfe sind noch nicht so viele.

Auszerdem steht auch immer noch irgendwie im Raum, ob die Kopf-Zahl-Situation wirklich symmetrisch ist. Bei 100 Wuerfen sind die statistischen Schwankungen noch so grosz, dass man darueber keine klaren Aussagen treffen kann.

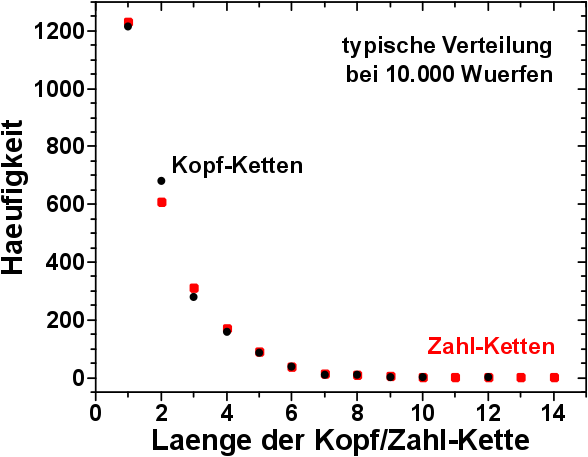
Schauen wir deswegen doch mal auf die Kopf- und Zahl-Kettenverteilungen fuer 10.000 Wuerfe:

Das ist zwar kein Beweis, aber fuer meine Belange reicht es, um davon auszugehen, dass tatsaechlich eine symmetrische Situation vorliegt und ich Zahl-Wuerfe im Weiteren ganz beruhigt unberuecksichtigt lassen kann.

Ach ja, die in diesem Bild gezeigten Kopf- bzw. Zahl-Kettenverteilungen sind selbstverstaendlich aus dem selben Experiment.

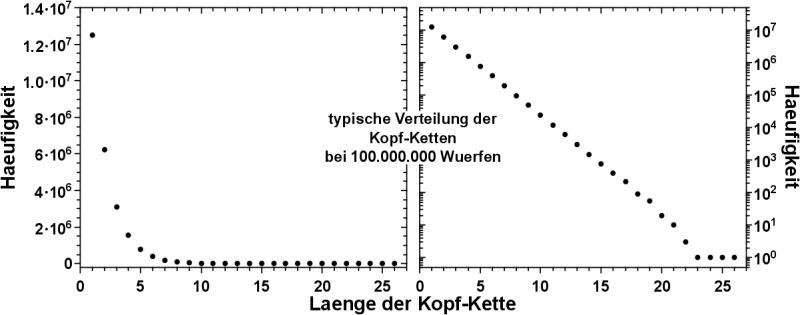
„Aber mhmmmm … das sieht ja verdaechtig aus“, dachte ich mir da und schaute mir mal die Situation bei 100 Millionen Wuerfen an.

Im linken Graphen (nicht zu verwechseln mit Graphen … tihihi) ist die Ordinatenachse linear und wir sehen das bereits bereits bekannte Verhalten.

Im rechten Graphen hingegen ist das selbe Experiment zu sehen, allerdings ist die Ordinatenachse logarithmisch. Jeder lange Strich bedeutet also eine Verzehnfachung des Wertes.

Und was sehen wir hier? WHOOOOAAAHHHH!!! Die Kopf-Kettenverteilung liegt auf einer Geraden. KRASSOMAT!

Das sieht aus, als ob das Universum mich an seinen ihren Geheimnissen teilhaben lassen will.

Bei so viel Eleganz war ich pløtzlich abgelenkt von den eigentlichen (Kasino) Fragen und konzentrierte mich nun darauf. War eh viel spannender.

Aber genug fuer heute. Mehr dazu im naechsten Beitrag in dieser Reihe.