Muenzwuerfe sind statistisch gut untersucht. Aber mit meinen Statistikkenntnissen ist’s nicht so weit her.
Und seit langer Zeit fragte ich mich, wie fair eine faire Muenze _zu mir_ ist.
Etwas konkreter fragte ich mich zwei Dinge:
1.: wie viel mehr ich „Kopf“ (oder „Zahl“ … im Weiteren ohne Anfuehrungszeichen) erhalte, und
2.: wie oft ich bspw. 3 mal, 4 mal, 5 mal etc. Kopf (oder Zahl) hintereinander werfe,
wenn ich eine faire Muenze bspw. 10 mal, 100 mal, 1000 mal, etc. werfe.
Ersteres bedeutet also das Folgende: wenn ich im Kasino immer nur auf Kopf setze, habe ich dann am Ende plus minus Null gewonnen oder verloren? Bei einer fairen Muenze wuerde ich das ganz naiv erstmal erwarten. Oder anders: ich erwarte also, dass, wenn ich einen Ueberschuss an Zahl habe, dies sich „automatisch“ ausgleicht.
Das Zweite ist die Frage danach wann ich Haus und Hof verspielt habe, wenn ich im Kasino immer auf Zahl setze und meinen Einsatz immer verdopple wenn Kopf kommt. Es geht hier also um Kopf-Ketten.
Mathematisch ist das sozusagen die Umkehrung des Prinips hinter Fellers Muenzwurfkonstanten.
Das ist alles schon geløst, aber wie ich oben schrieb, fehlt mir das mathematische Wissen.
Also dachte ich mir, dass ich ein paar anschauliche Experimente mache.
Ich programmierte mir ein kleines Programm, welches fuer mich die Muenze ganz oft warf und registrierte ob es Kopf oder Zahl war. Auszerdem wurde die Verteilung der Kopf-Ketten (und auch der Zahl-Ketten) gespeichert.
Ein Beispiel (50 Wuerfe):
ZKKKKZZKZKZKZKZKZKKZZZKKZKKZKZZZKZZKKZZKKKKZKZKZKZ
Nicht gespeichert wurde das konkrete Resultat jedes Wurfes.
Gespeicherte wurde aber:
| Laenge der Kette | Haeufigkeit dieser Kopf-Kette | Haeufigkeit dieser Zahl-Kette |
|---|---|---|
| 1 | 12x | 10x |
| 2 | 3x | 4x |
| 3 | 2x | 0x |
| 4 | 0x | 2x |
Und auch wenn diese Information bereits in der Tabelle steckt, so wurde nochmal extra gespeichert, dass Kopf zwei mal øfter geworfen wurde als Zahl.
Nun habe ich das Programm natuerlich nicht nur eine Muenze bswp. 10 Millionen mal werfen lassen.
Nein, nein. Da das Werfen schon automatisiert war, wollte ich auch wissen, ob es das Gleiche ist, wenn eine Muenze 10 mal geworfen wird und dies 10 mal wiederholt wird oder ob ich eine Muenze gleich 100 mal werfe.
Ganz konkret liesz ich die Muenze 10 mal, 100 mal, 1.000 mal, …, 10.000.000 mal werfen und dies wurde jeweils 1.000 mal wiederholt.
Auszerdem liesz ich die Muenze 100.000.000 mal, 1.000.000.000 mal und 10.000.000.000 mal werfen und wiederholte dies jeweils 100 mal, 10 mal und gar nicht.
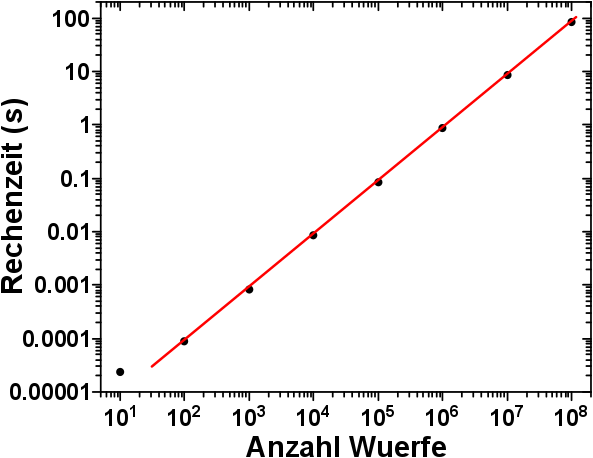
Dass die letzten Experimente nicht so oft wiederholt wurden liegt daran, wie viel Zeit so ein Experiment braucht:
Wenn ich die Muenze 10 Millionen mal werfe und das Experiment 1000 mal wiederhole, so benøtigt das ca. 10.000 Sekunden. Das sind beinahe 3 Stunden. Weil ich meinen Computer nicht mehr als ca. 10 Stunden rechnen lassen wollte, verminderte ich die Anzahl der letzten drei Experimente.
Genug fuer heute. Beim naechsten Mal zeige ich euch, meinen lieben Leserinnen und Lesern, dann wie typische Resultate aussahen.
Leave a Reply