Søren in Norwegen

Jippie! Ich hatte doch noch ein Bild:

Das Bild der Toilette habe nicht ich gemacht, sondern die junge Dame, welcher der Taschencomputer gehørte, auf dessen Bildschirm das Bild der Toilette abgebildet ist.

Und das Bild vom Bild der Toilette auf dem Bildschirm des Taschencomputers machte ich ebenso nicht, sondern der junge Mann der bei mir wohnt.

Diesen Eintrag wollte ich schon laenger schreiben (seit ca. Januar 2016), der blieb aber immer und immer wieder liegen.

Am Anfang fehlte die Fotos und dann hatte ich immerzu andere Dinge, ueber die ich lieber schreiben wollte.

Es geht um meine selbstmontierten Scheibenbremsen. Hier ist die fuer das Vorderrad zustaendige Bremse:

Seit vielen Jahren wollte ich Scheibenbremsen haben. Hubert kaufte ich aber zu einer Zeit, als diese noch relativ neu waren fuer Fahrraeder. Oder zumindest in 2005 waren in der Preisklasse in der sich Hubert befand Scheibenbremsen eher ungewøhnlich.

Huberts Rahmen erlaubte zwar eine Scheibenbremse fuer das Vorderrad, aber nicht fuer das Hinterrad.

Im Winter 2015 dachte ich dann zum ersten Mal wirklich und wahrhaftig daran, mir ein Neues Fahrrad zu kaufen. Der Hauptgrund war, dass ich nun auch im Winter mit dem Fahrrad fuhr und die Bedingungen mit Schnee und Eis und Matsch und Kaelte hier deutlich anders sind als anderswo im Winter. Da wollte ich lieber Scheibenbremsen haben. Das fuehlte sich sicherer an.
Auszerdem stand ohenhin eine grøszere Investition an, denn der Aluminiumrahmen meiner Raeder war durch langjaehriges Bremsen bereits so duenn geworden, dass mir ein (sehr) Vielfahrradfahrer sagte, dass er da nicht mehr mit fahren wuerde.

Und auch wenn jede Menge Sachen an Hubert ohnehin nicht mehr original waren, so tat es mir doch im Herzen weh ein komplett neues Velociped zu kaufen, denn (vor allem) der Rahmen war ja noch gut.

Besagter Vielfahrradfahrer machte mich dann aber drauf aufmerksam, dass es Adapter fuer soche Rahmen wie Huberts gibt, sodass die Montage einer Scheibenbremse auch fuer hinten møglich ist.

Zusammen mit dem Angebot, dass er mich bei der Montage anleitet (denn ich wollte so gerne selber schrauben :) ) dachte ich dann: .oO(JIPPIEE!!! Hubert wird leben!)

Und hier ist sie:

Der Adapter ist deutlich zu erkennen.

Leider, leider, leider, ist Hubert zum Zeitpunkt als ich dies schreibe (2017-03-30) unheilbar krank und muss nun doch sterben.

Das Kugellager fuer die Lenkeinrichtung ist kaputt und der Vielfahrradfahrer meint, dass das Innere des Rahmens, dort wo die Kugeln drin rollen vermutlich irreparabel beschaedigt ist. Das Kugellager selbst kønnte zwar prinzipiell ausgetauscht werden, es wuerde aber langfristig Nichts bringen. Hinzu kommt, dass Hubert so alt und Teile fuer Fahhrraeder nicht standardisiert sind, sodass es eher schwer werden wuerde, ein neues Kugellager zu besorgen.

Das finde ich sehr schade. Aber zum Zeitpunkt des Schreibens ist noch nichts entschieden. Ich werde Hubert so lange wie møglich fahren :) . Liegt mir mein Fahrrad doch sehr am Herzen.

Slalom sieht gefaehrlich aus. Und wenn ich da mit dem jungen Mann der bei mir wohnt um die Wette den Berg runter sause, dann fuehlt’s sich auch so an.

Aus Prinzip und fuer’s bessere Gefuehl trage ich deswegen einen Helm. Und bei ein paar ungeplanten Stuerzen, bei denen der Kopf auf den doch eher harten Untergrund knallte, hat mich Selbiger auch auch schon vor schlimmeren Kopfverletzungen bewahrt.

Gegen blendenden Schnee, Sonne in die Augen und den Wind hilft eine Brille ganz famos. Damit kann man dann auch noch schneller den Berg runter fahren.

Und weil Schlange stehen zum Ausleihen solcher Sachen doof ist, habe ich mir die nøtige Ausruestung dann selbst gekauft:

Und so sehe ich damit aus:

Toll wa!

.oO(Wird Zeit, dass’s wieder schneit!)

Neulich stolperte ich ueber einen Artikel mit dem Titel „A Self-Made Man„. Darin wird beschrieben wie Norah Vincent im Stil eines Guenter Wallraff fuer 18 Monate „undercover“ als Mann (mit neuem Namen „Ned“) unter Maennern lebt …

[…] to see what life was like on the other side of the gender divide.

Einen editierten Auszug aus dem Buch mit dem gleichnamigen Titel kann hier gelesen werden.

Interessant finde ich, wie sie, von „der anderen Seite“ aus, es empfand, sich mit Frauen zu treffen.

Vincent said the dates were rarely fun and that the pressure of „Ned“ having to prove himself was grueling. She was surprised that many women had no interest in a soft, vulnerable man.

In dem Zusammenhang schreibt sie ebenso, dass auch Menschen des gleichen Geschlechts oft genug nicht wirklich verstehen, was vor sich geht.

„My prejudice was that the ideal man is a woman in a man’s body. And I learned, no, that’s really not. There are a lot of women out there who really want a manly man, and they want his stoicism,“ she said.

Und noch eine andere Erfahrung scheint „in Echt“ gravierender zu sein als in der Theorie, denn …

[s]he was quickly reminded that in this arena, it’s women who have the power, she said.

Oder wie sie es ausdrueckt:

„In fact, we sit there and we just with one word, ’no,‘ will crush someone,“ she said. „We don’t have to do the part where you cross the room and you go up to a stranger that you’ve never met in the middle of a room full of people and say the first words. And those first words are so hard to say without sounding like a cheeseball or sounding like a jerk.“

Wenn man denn eine Zusammenfassung ihrer Erlebnisse schreiben møchte, so kønnte es vielleicht diese sein:

Norah began to empathize with the fear and stress men feel for having to always be the strong provider.

Das ist alles interessant und sehr praktisch.

Viel spannender fand ich aber, das es Aspekte gab, die nicht so richtig zu greifen waren. Einer dieser Aspekte war natuerlich, dass sie sich als jemand ausgab, der sie nicht war.

„The pressure of being someone that you’re not and … the fear of discovery and the deceit that it involves piles up and piles up. […]“

Mich duenkt auch Guenter Wallraff schreibt darueber.

Bei Norah Vincent fuehrte dies zu einer Depression. Als Ursache schlussfolgerte sie, dass man mit seiner Identitaet nicht herum spielt:

„When you mess around with that, you really mess around with something that you need that helps you to function. […]“

Und welches Gender wir sind ist ein verdammt wichtiger Teil unserer Identitaet!

Aber am Allerwichtigsten fand ich eine Sache, die ich hier schon so oft ansprach:

“ […] [a]nd I found out that gender lives in your brain and is something much more than costume.“

Unser Gehirn aber ist nicht nur durch unsere Gene (oder physikalisch/chemische Umwelteinfluesse) bestimmt, sondern auch durch die Gesellschaft in der wir aufwachsen. Gluecklich kønnen sich die schaetzen, bei denen das genetisch bestimmte Gender uebereinstimmt mit dem was die Gesellschaft erwartet.

Aber es ist ja nicht nur, dass „die Leute“ bestimmte Vorstellungen davon haben, wer mit wem ficken oder welches Geschlechtsteil haben „darf“. Oder auf welche Toilette jemand gehen oder welche Kleidung jemand anziehen „sollte“. Diese Dinge sind relativ direkt mit dem (sehr breiten) sexuellen „Phasenraum“ der Identitaet verknuepft.
Die Gesellschaft erwartet noch ganz andere Dinge bezueglich der Identitaet einer Person. Derartige Erwartungen basieren darauf, ob diese Person maennliche oder weibliche primaere Geschlechtsmerkmale entwickelte oder nicht (und denke da mal niemand, dass dies nur davon abhaengig waere ob das 23’ste Chromosomenpaar „XX“ oder „XY“ ist).
So wie bspw. hier:

Beim letzten Mal schrieb ich ueber die (eher zufaellige) Entdeckung der versteckten Eleganz des Universums in Muenzwuerfen.

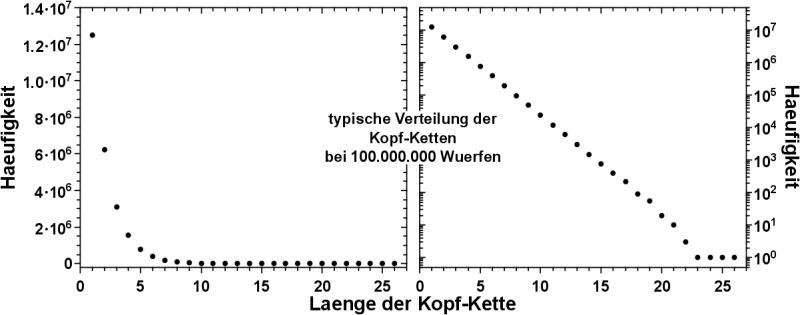
Dies konnte ich natuerlich nicht einfach so auf sich belassen und schaute mir mal an, wie das bei Experimenten unterschiedlicher Laenge aussieht:

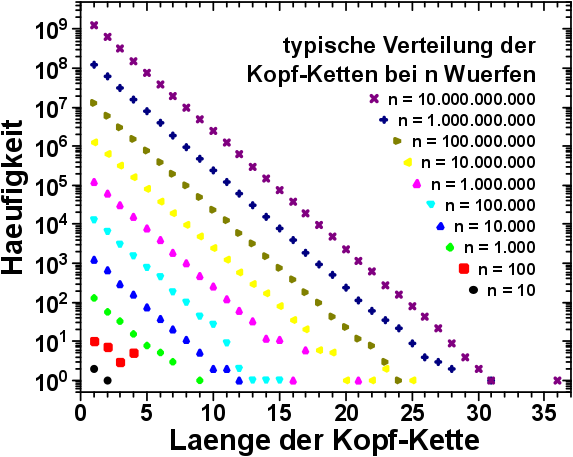
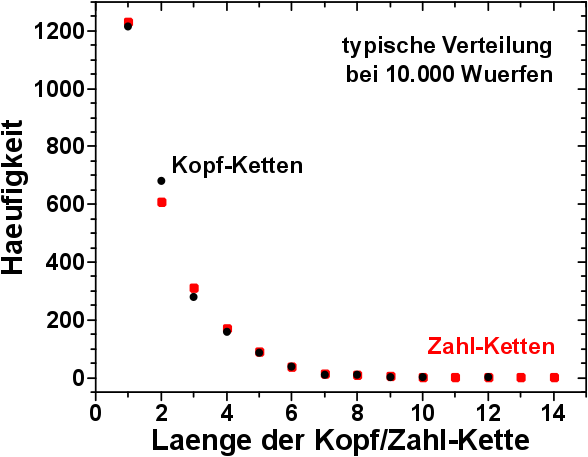
Die Verteilungen der Kopf-Ketten bei unterschiedlich lang dauernden Experimenten sind parallel zueinander. Da muss also mehr dahinter stecken.

Wenn bei logarithmischer Darstellung Geraden zu sehen sind, dann faellt mir als Physiker natuerlich erstmal ein, diese mittels einer exponentiellen Funktion zu modellieren. In diesem Fall waere es natuerlich ein exponentieller Zerfall und das sieht so aus:

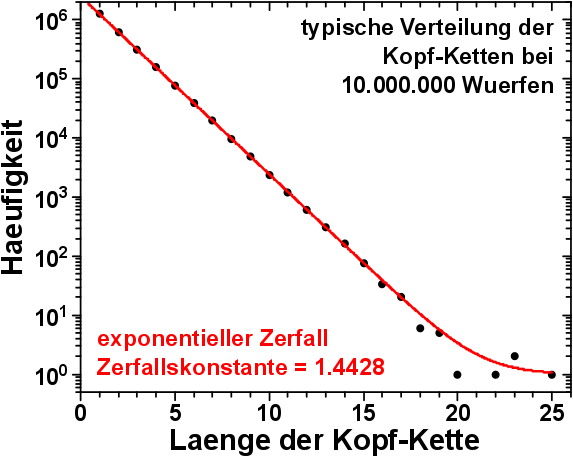
Das Reziproke der Zerfallskonstante ist 0,6931. Und das war mir verdaechtig nahe dem Wert der Standardabweichung der Normalverteilung.

Also dachte ich, dass da mehr dahinter steckt. Dass møglichwerweise in der Zerfallskonstante irgendwie die angenommene Wahrscheinlichkeitsverteilung liegt.

Das war so nicht ganz richtig, aber auch nicht vøllig daneben. Zu Letzterem aber mehr in einem spaeteren Beitrag. An dieser Stelle sei nur so viel gesagt, dass ich ein paar Ueberlegungen anstellte und noch mehr Experimente machte, dies mich aber dem Geheimnis hinter dem Wert der Zerfallskonstante nicht naeher brachte.

Also fasste ich allen Mut zusammen und sprach mal mit einem Mathematikexperten darueber. Zufaelligerweise .oO(Wortspielkasse!) war gleich der erste Experte mit dem ich sprach, Øyvind Bakke, ein Professor der sich professionel mit Statistik beschaeftigte.

Als ich mein Problem beschrieb, hatte er nicht gleich die Løsung parat. Aber die trudelte wenig spaeter per elektronischer Post ein.

Natuerlich ist das, mit dem ich hier auf meinem niedriegen Niveau spiele, schon lange erforscht. Und die vermutete Eleganz ist tatsaechlich vorhanden. Aber dafuer muss ich etwas weiter ausholen und leider (?) zum ersten Mal in diesem Weblog mit Formeln arbeiten.

Traditionellerweise wird die Wahrscheinlichkeit, mit der ein Ergebniss eintritt als \(p\) bezeichnet. Das steht møglicherweise fuer „probability“. Die Wahrscheinlichkeit, dass ein Ereignis eintritt, kann niemals grøszer sein als 100%.
Wenn mehrere Ereignisse eintreten kønnen, so ist die Summe aller Wahrscheinlichkeiten 100%. Da man immer das Resultat „es passiert nichts“ mit einbeziehen muss, ist also garantiert, dass immer irgendwas passiert … Tihihihi.
Bei einem Muenzwurf kønnen nur zwei Ereignisse eintreten. Die Wahrscheinlichkeit fuer „Zahl“ sei mit \(p\) bezeichnet. Die Wahrscheinlichkeit fuer „Kopf“ ist dann natuerlich 100% minus die Wahrscheinlichkeit fuer Zahl. Da 100% gleich 1 (eins) ist, kann man dies schick schreiben als \((1-p)\).
Im Fall einer fairen Muenze ist diese Wahrscheinlichkeit \(p\) natuerlich 1/2, aber ich møchte zunaechst auf dieser etwas abstrakten Ebene verbleiben.

Wenn Kopf liegt, dann betraegt die Wahrscheinlichkeit Zahl im naechsten Wurf zu bekommen: \(p\).
Wenn Kopf liegt, dann betraegt die Wahrscheinlichkeit nochmals Kopf im naechsten Wurf zu bekommen: \((1-p)\).
Die Wahrscheinlichkeit, dass man, wenn Kopf bereits liegt, bei zwei weiteren Wuerfen Kopf und dann Zahl bekommt ist also: \((1-p)\cdot p\). Dies ist die Wahrscheinlichkeit fuer eine Kopf-Kette der Laenge 2. Nicht vergessen, es lag bereits Kopf und wir haben dazu noch zwei Wuerfe dazu genommen und im letzten Wurf wurde die Kette mit Zahl abgebrochen.
Die Wahrscheinlichkeit, dass man, wenn Kopf bereits liegt, bei drei weiteren Wuerfen Kopf, nochmals Kopf und dann Zahl bekommt ist: \((1-p)\cdot (1-p) \cdot p\). Dies ist die Wahrscheinlichkeit fuer eine Kopf-Kette der Laenge 3.
Dies setzt sich weiter fort und die Wahrscheinlichkeit eine Kopf-Kette der Laenge \(n\) zu erhalten ist somit: \((1-p)^{(n-1)}\cdot p\).

Dies ist eine sogenannte geometrische Verteilung.

Meine empirischen Experimente kann man nun interpretieren als Frequenz \(f\), wie oft eine Kopf-Kette der Laenge \(n\) auftritt.

Da ich die Frequenz logarithmisch aufgetragen (und wichtiger mittels eines exponentiellen Zerfalls modelliert) habe erhalte ich also:

\(\ln f = \ln \left[ (1-p)^{(n-1)} \cdot p\right] = (n-1)  \cdot \ln(1-p) + \ln p\).

Um die Abbildung und insbesondere den Verlauf der roten Kurve zu beschreiben, muss man im Hinterkopf haben, dass in diesem Falle \(n\) das Argument und \(f\) der Funktionswert ist.
Benutzen wir nun ganz konkret 1/2 als die Wahrscheinlichkeit Zahl zu werfen ein, so erklaert sich der Wert fuer den „Abfall“ der Modellierungskurve – die Zerfallskonstante (oder vielmehr das Reziproke der Zerfallskonstante). Der Logarithmus naturalis von 2 ist naemlich ungefaehr 0,6931.
Warum ich jetzt das Reziproke der Zerfallskonstante betrachtet habe, haengt damit zusammen, wie man den exponentiellen Zerfall definiert. Oft wird dieser naemlich mit einem Bruch im Exponenten geschrieben und wenn man den nicht haben will, nimmt man einfach den reziproken Wert. Aber ich verliere mich hier gerade etwas in Details.

Passen wir  nun den im vorherigen Bild gezeigten Datensatz mit dem richtigen Modell an, so erhalten wir:

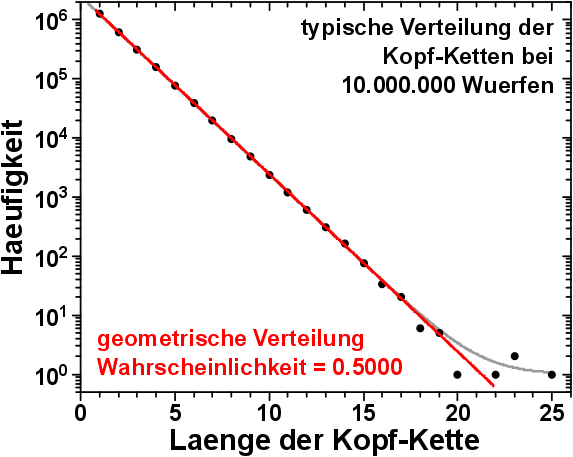
YEAH!!! Das passt ja super!
Die graue Kurve ist der bereits oben besprochene exponentielle Zerfall, denn ich finde es schon interessant, wie sich zwei vøllig verschiedene Modelle (und damit Implikationen) der Realitaet doch ziemlich gut annaehern. Das ist so wie der Unterschied zwischen den Gravitationstheorien von Newton und Einstein. Beides sind nur Modelle und Newton ist definitiv mehr falsch als Einstein. Aber wenn ich mich nur in Bereichen bewege, in denen das nicht relevant ist, muss ich mich  nicht mit der komplizierteren Sache herumschlagen. Toll wa!

Nun da die Neugier, wo die Eleganz des Universums herkommt, befriedigt ist, komme ich zurueck zum eigentlichen Thema: „Wie unfair ist eine Muenze zu mir, wenn ich diese werfe?“

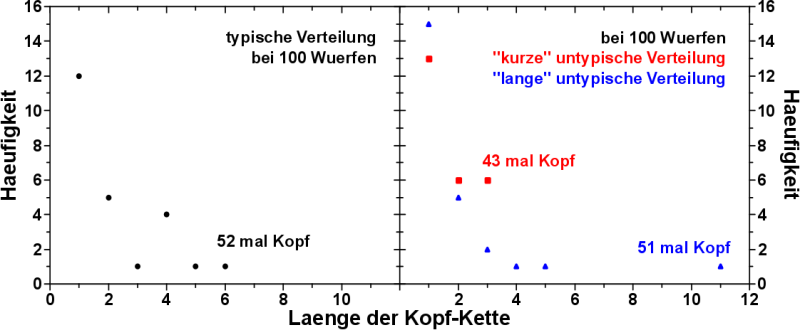
Dies ist in diesem Bild veranschaulicht:

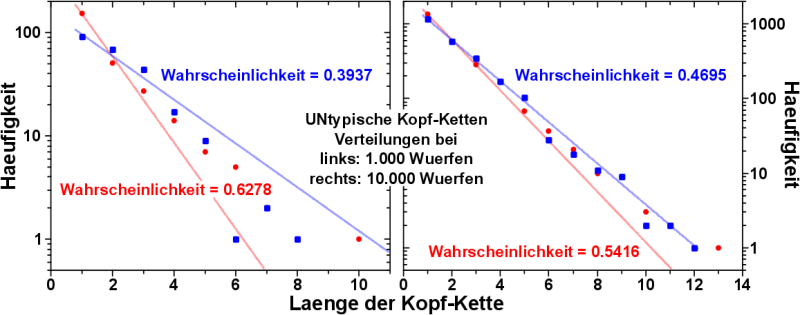
Hier sind untypische Kopf-Ketten Verteilungen fuer jeweils zwei Experimente (aus jeweils 1.000)  mit jeweils 1.000 bzw. 10.000 Wuerfen dargestellt. Denn 1.000 Mal eine Muenze werfen ist durchaus etwas, was man machen kann. Da braucht man nur eine Klasse mit 10 Schuelern und laeszt die 100 Mal ’ne Muenze werfen. Bzw. macht man das 10 Jahre lang, dann hat man 10.000 Muenzweurfe.

Passt man die Ergebnisse mittels der geometrischen Verteilung an, um den Wahrscheinlichkeitswert fuer Zahl heraus zu bekommen, so kønnen sich diese Werte massiv voneinander unterscheiden. Ich muss zugeben, dass die hier gezeigten Werte nicht nur untypisch, sondern extrem waren, suchte ich doch extra die grøszten / kleinsten Wahrscheinlichkeitswerte unter all den jeweils 1.000 Experimenten heraus.

Die extremen Wahrscheinlichkeitswerte fuer die Daten im linken Graphen bedeuten, dass selbst bei 1.000 Wuerfen mit einer eigentlich fairen Muenze, die Schwankungen so extrem sein kønnen, dass es aussieht, dass die Muenze NICHT fair ist, sondern eine (erhebliche!) Tendenz zu einem der beiden Resultate hat. Und dabei denkt man doch landlaeufig (also zumindest ich dachte das bisher), dass 1.000 Wuerfe schon ’ne gute Statistik sind.

An den Wahrscheinlichkeitswerten im rechten Graphen sieht man aber auch, dass die extremen Werte weiter zusammen ruecken. Untypische Kopf-Ketten Verteilungen werden also immer typischer. Im Falle des 1.000-mal-10-Millionen-Wuerfe-Experiments betrug die Diskrepanz zwischen den beiden extremsten Wahrscheinlichkeitswerten uebrigens nur noch ca. 0,0021.

Aber 10 Millionen Wuerfe. Da braucht man schon die Schueler eines ganzen Landes fuer um das zu realisieren … .oO(MUAHAHAHAHAHA).

Die gibt es seit Jahren, und ich habe immer gesagt, dass sie den Menschen an der Kasse ersetzen werden.

Aber erst in letzter Zeit ist mir aufgefallen, dass es tatsaechlich weniger Kassenpersonal gibt.

Und wer hat’s entwickelt und gebaut? So Leute wie ich: Ingenieure und Softwareentwickler. Weil wir eigentlich eine bessere Welt schaffen wollen. Nur mit den direkten Konsequenzen unserer Arbeit wollen wir nicht so gerne konfrontiert werden.

Aber ich habe ein bisschen die Hoffnung, dass andere wichtigerere Leute als Ingenieure, das mehr und mehr merken und versuchen Wege der Anpassung an die neue Situation zu finden. Wie bspw. in Finnland. Auch wenn die vorgeschobenen Motive (und vermutlich glauben die Politiker da wirklich dran) bisher immer noch sog. „Kosteneinsparungen“ sind *rolleyes*.

Auch wichtig in diesem Fall ist, dass das die Mitte-Rechts-Regierung macht. Und das ist der Hauptgrund, warum ich auf die Situation auf der anderen Seite des Atlantiks mit etwas Hoffnung sehe. Ihr wisst schon, Nixon und China und so.

Es steht die Frage im Raum, wie oft ich bspw. 3 mal hintereinander Kopf (oder Zahl) werfe, wenn ich eine Muenze 100 Mal werfe.

Hintergrund dieser Frage ist immer noch, wie schnell ich pleite gehe, wenn ich all mein Geld auf das jeweils andere Resultat setze und bei jedem Kopf-Wurf meinen Einsatz verdopple.

Und natuerlich interessieren mich nicht nur Ketten von 3-mal-Kopf-(oder-Zahl)-hintereinander, sondern auch alle anderen møglichen Kopf-(oder Zahl)-Ketten.

Und damit ich mir das „(oder Zahl)“ im Weiteren sparen kann, konzentriere ich mich ab sofort im Wesentlichen nur noch auf die „Kopf“-Wuerfe.
Man kann sich ja denken, dass die Kopf-Zahl-Situation mehr oder weniger symmetrisch ist. Innerhalb statistischer Schwankungen, ist das auch erstmal richtig. Mehr dazu in einem viel spaeteren Beitrag.

Bei 100 Wuerfen sieht eine typische Kopf-Kettenverteilung so aus wie der linke Graph in diesem Bild:

So einige Male folgte auf Kopf gleich eine Zahl, ein paar Mal folgt auf einen Kopf Wurf gleich noch einer. Høhere Kopf-Ketten treten zwar auf, aber selten.

Zwei untypische (aber innerhalb statistischer Schwankungen durchaus erlaubte) Kopf-Kettenverteilung kann man im rechten Graph sehen.

Bei einer von mir als „kurz“ bezeichneten untypischen Kopf-Kettenverteilung treten keine høheren Kopf-Ketten auf, waehrend bei einer „langen“ untypischen Kopf-Kettenverteilung ein unwahrscheinlich „hohes“ Ereigniss auftritt. In diesem Fall wurde bei letzterem 11 mal hintereinander Kopf geworfen … oioioi … 2¹¹, je nach Ausgangseinsatz ist das schon ’ne ganze Menge Zaster.

Aber das ist natuerlich noch keine Antwort auf die Frage. 100 Wuerfe sind noch nicht so viele.

Auszerdem steht auch immer noch irgendwie im Raum, ob die Kopf-Zahl-Situation wirklich symmetrisch ist. Bei 100 Wuerfen sind die statistischen Schwankungen noch so grosz, dass man darueber keine klaren Aussagen treffen kann.

Schauen wir deswegen doch mal auf die Kopf- und Zahl-Kettenverteilungen fuer 10.000 Wuerfe:

Das ist zwar kein Beweis, aber fuer meine Belange reicht es, um davon auszugehen, dass tatsaechlich eine symmetrische Situation vorliegt und ich Zahl-Wuerfe im Weiteren ganz beruhigt unberuecksichtigt lassen kann.

Ach ja, die in diesem Bild gezeigten Kopf- bzw. Zahl-Kettenverteilungen sind selbstverstaendlich aus dem selben Experiment.

„Aber mhmmmm … das sieht ja verdaechtig aus“, dachte ich mir da und schaute mir mal die Situation bei 100 Millionen Wuerfen an.

Im linken Graphen (nicht zu verwechseln mit Graphen … tihihi) ist die Ordinatenachse linear und wir sehen das bereits bereits bekannte Verhalten.

Im rechten Graphen hingegen ist das selbe Experiment zu sehen, allerdings ist die Ordinatenachse logarithmisch. Jeder lange Strich bedeutet also eine Verzehnfachung des Wertes.

Und was sehen wir hier? WHOOOOAAAHHHH!!! Die Kopf-Kettenverteilung liegt auf einer Geraden. KRASSOMAT!

Das sieht aus, als ob das Universum mich an seinen ihren Geheimnissen teilhaben lassen will.

Bei so viel Eleganz war ich pløtzlich abgelenkt von den eigentlichen (Kasino) Fragen und konzentrierte mich nun darauf. War eh viel spannender.

Aber genug fuer heute. Mehr dazu im naechsten Beitrag in dieser Reihe.

… von denen ich dachte, dass ich die niemals lesen werde:

1.: Russia Is Running Out of Forest

2.: Saudis ‚fear sand shortage‘

3.: An Interview with a Gay, Russian Neo-Nazi … .oO(DA FUCK!)

… tihihihi …

Wenn ihr, meine lieben Leserinnen und Leser, nur einen der drei Links anklicken wollt, dann empfehle ich das Interview. Und sei es nur um sich deren Symbol anzuschauen: das zu erwartende Hakenkreuz im trauten Beisammensein mit gekreuzten, erigierten Schwaenzen Penissen Schwaenzen .oO(verfluchte Sozialisation). Aber auch das Interview selber lohnt sich zu lesen (sind auch nur zwei Seiten). Denn der Titel laeszt nur die Haelfte des Spasz‘ erahnen. Da jagt eine Schote die Andere, wie man, da wo ich herkomme, so schøn sagt.

Muenzwuerfe sind statistisch gut untersucht. Aber mit meinen Statistikkenntnissen ist’s nicht so weit her.

Und seit langer Zeit fragte ich mich, wie fair eine faire Muenze _zu mir_ ist.

Etwas konkreter fragte ich mich zwei Dinge:
1.: wie viel mehr ich „Kopf“ (oder „Zahl“ … im Weiteren ohne Anfuehrungszeichen) erhalte, und
2.: wie oft ich bspw. 3 mal, 4 mal, 5 mal etc. Kopf (oder Zahl) hintereinander werfe,
wenn ich eine faire Muenze bspw. 10 mal, 100 mal, 1000 mal, etc. werfe.

Ersteres bedeutet also das Folgende: wenn ich im Kasino immer nur auf Kopf setze, habe ich dann am Ende plus minus Null gewonnen oder verloren? Bei einer fairen Muenze wuerde ich das ganz naiv erstmal erwarten. Oder anders: ich erwarte also, dass, wenn ich einen Ueberschuss an Zahl habe, dies sich „automatisch“ ausgleicht.

Das Zweite ist die Frage danach wann ich Haus und Hof verspielt habe, wenn ich im Kasino immer auf Zahl setze und meinen Einsatz immer verdopple wenn Kopf kommt. Es geht hier also um Kopf-Ketten.
Mathematisch ist das sozusagen die Umkehrung des Prinips hinter Fellers Muenzwurfkonstanten.

Das ist alles schon geløst, aber wie ich oben schrieb, fehlt mir das mathematische Wissen.

Also dachte ich mir, dass ich ein paar anschauliche Experimente mache.

Ich programmierte mir ein kleines Programm, welches fuer mich die Muenze ganz oft warf und registrierte ob es Kopf oder Zahl war. Auszerdem wurde die Verteilung der Kopf-Ketten (und auch der Zahl-Ketten) gespeichert.

Ein Beispiel (50 Wuerfe):

ZKKKKZZKZKZKZKZKZKKZZZKKZKKZKZZZKZZKKZZKKKKZKZKZKZ

Nicht gespeichert wurde das konkrete Resultat jedes Wurfes.

Gespeicherte wurde aber:

Und auch wenn diese Information bereits in der Tabelle steckt, so wurde nochmal extra gespeichert, dass Kopf zwei mal øfter geworfen wurde als Zahl.

Nun habe ich das Programm natuerlich nicht nur eine Muenze bswp. 10 Millionen mal werfen lassen.

Nein, nein. Da das Werfen schon automatisiert war, wollte ich auch wissen, ob es das Gleiche ist, wenn eine Muenze 10 mal geworfen wird und dies 10 mal wiederholt wird oder ob ich eine Muenze gleich 100 mal werfe.

Ganz konkret liesz ich die Muenze 10 mal, 100 mal, 1.000 mal, …, 10.000.000 mal werfen und dies wurde jeweils 1.000 mal wiederholt.
Auszerdem liesz ich die Muenze 100.000.000 mal, 1.000.000.000 mal und 10.000.000.000 mal werfen und wiederholte dies jeweils 100 mal, 10 mal und gar nicht.

Dass die letzten Experimente nicht so oft wiederholt wurden liegt daran, wie viel Zeit so ein Experiment braucht:

Wenn ich die Muenze 10 Millionen mal werfe und das Experiment 1000 mal wiederhole, so benøtigt das ca. 10.000 Sekunden. Das sind beinahe 3 Stunden. Weil ich meinen Computer nicht mehr als ca. 10 Stunden rechnen lassen wollte, verminderte ich die Anzahl der letzten drei Experimente.

Genug fuer heute. Beim naechsten Mal zeige ich euch, meinen lieben Leserinnen und Lesern, dann wie typische Resultate aussahen.

Algerien? Die Menschen dort gehøren doch alle dem Islam an, nicht wahr. Das muss ja furchtbar sein fuer die Frauen!

Interessant, dass 70 % der Menschen die dort den Anwaltsberuf ausueben, und 60 % der Leute im Richterberuf, weiblichen Geschlechts sind.

Da frage ich mich doch, ob das nicht auch hier bei „uns“ ginge.

Mich beschleicht das Gefuehl, dass die Antwort darauf auf lange Zeit noch ein „Nein!“ sein wird.

Und mich duenkt, dass es auch mit dem ganzen Themenkomplex hierum zu tun hat: