Søren in Norwegen

Lang und breit habe ich mich hier darueber ausgelassen, wie dumm doch der Computer ist und was ich mir ueberlegen musste, um den dazu zu bringen, das zu machen, von dem ich wollte, dass es gemacht wird.

Irgendwann hab ich dann mal mit einem erfahreneren Programmierer (ich mag nicht „richtiger Programmierer“ sagen, denn ich programmiere ja auch richtig) geredet. Und der hat mir mal die Nuetzlichkeit des Konzepts von sog. „Dictionaries“ naeher gebracht.
Das war mir vorher schon bekannt. Ich hatte darueber schon gelesen und formal hatte ich das auch begriffen. Aber die Fibonacciuebung war das „erste Programmierding nach einer laengeren Pause“ und da griff ich natuerlich auf Konzepte zurueck, die mir wohlbekannt waren.

Die Tabelle im obigen verlinkten Beitrag ist ja im Wesentlichen ein dreidimensionales Feld. Der Computer unterscheidet zuerst wie lang die zu untersuchende Zeichenkette sein soll, dann, welche Zeichenkette es ist und letztlich wie oft die vor kommt.
Schlieszlich muss dann zwischen Zahlen und Zeichen unterschieden werden Zeichenketten („0002“) wurden in Zahlen (2) umgewandelt usw. usf. Ich beschrieb das ja alles schon.

Bei einem Dictionary hab ich diesen ganzen Kram nicht. Ein Dictionary merkt sich halt einen Eintrag und was dann dazu steht. Sozusagen so:

„1“ : 15 mal, „2“ : 3 mal, … , „002“ : 5 mal, … , „0007“ : 35098 mal, …

Der Vorteil liegt also auf der Hand: Zeichenketten mit fuehrenden Nullen kønnen direkt so behandelt werden. Es muss also kein „Trick“ ausgedacht werden, der das „Abschneiden von fuehrenden Nullen“ bei der Umwandung von Zeichenkette zu Zahl beruecksichtigt.

Ein weiterer Vorteil eines Dictionary ist, dass ich auf ein bestimmtes Element ganz einfach und direkt zugreifen kann. Kommt in der Folge also bspw. die Zeichenkette „0345“ vor, so schlage ich im Dictionary nach, wie der Wert von „0345“ ist (und erhøhe den dann um eins). Ich muss also nicht erst herausfinden, in welchem Feld denn nun die Erhøhung stattfinden muss.

Dies alles macht den Code deutlich lesbarer und spart vor allem Rechenzeit.

Ich habe die Rechenzeiten fuer die verschiedenen Parameter nochmals analysiert und die hier angegebenen Zeiten wurden auf 1/3 reduziert.

Das ist zwar keine Grøszenordnung, aber doch betraechtlich.

Toll wa! Was man alles lernen kann, wenn man mal mit Leuten redet, die sich auskennen.

 

Als Abschluss dieser Miniserie møchte ich gern auf ein Artefakt der Datenaufbereitung aufmerksam machen.

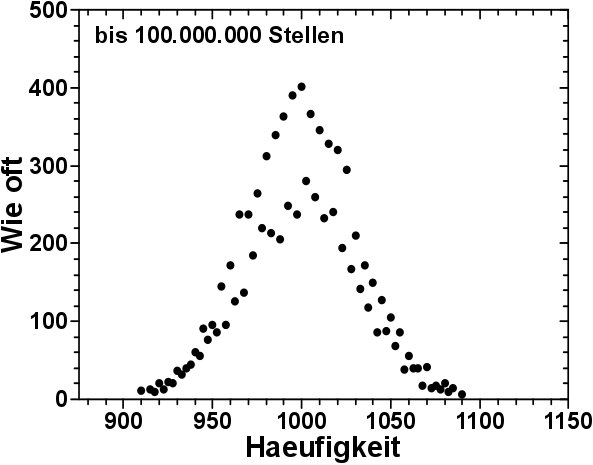
Wie hier erwaehnt, erstellte ich ein Histogramm der Daten. Ansonsten waere das alles naemlich nicht vernuenftig darstellbar / zu interpretieren gewesen. Dabei werden die Daten in eine bestimmte Anzahl (ich waehlte 100) gleich weite „Balken“ auf der Abzisse eingeteilt. Alles soweit ok und erstmal kein Problem.

Manchmal jedoch kommt es so vor, dass die Weite der Balken derart ist, dass (ehr vereinfacht ausgedrueckt) jeder zweite Wert „links“ der Grenze gezaehlt wird und die restlichen Werte „rechts“ der Grenze. Das Ganze sieht dann so aus:

Eine Art „Doppelpeak“.
Da hab ich natuerlich erstmal nicht schlecht geguckt.

Aber das laeszt sich ganz leicht løsen, indem man entweder die Breite der Balken veraendert, oder die Startpunkte aller Balken um einen gewissen Wert verschiebt.

Ich fand das witzig und wollte es euch, meinen lieben Leserinnen und Lesern, nicht vorenthalten.

 

Das war es dann nun tatsaechlich mit der Analyse der Fibonaccifolge.

Das war eigentlich mehr so fuer mich die Dokumentation einer Sache, welche mir in allen Punkten (Idee entwicklen, programmieren, Fehler entdecken und ueberwinden und letztlich die erhaltenen Daten auswerten) grosze Freude bereitete. Und einen Teil der Freude wollte ich auch gern weitergeben.