Nun rechnete und rechnete mein kleiner braver Laptop 15 Stunden ohne Unterbrechung und heraus kamen viele Zahlen.
Es werden nur noch die Daten fuer vierstellige Zeichenfolgen betrachtet.
Drei-, zwei- und einstellige Zeichenfolgen passen in das Modell gut rein, es sieht aber nicht so schøn aus. Also vom aesthetischen Anspruch mein ich.
Dies, weil sich bei nur 1.000, 100 bzw. 10 Datenpunkten statistische Schwankungen noch deutlich negativ auf das Erscheinungsbild auswirken kønnen, selbst wenn diese einer Normalverteilung folgen und mathematisch somit alles in Ordnung ist. Bei 4-stelligen Zeichenketten habe ich aber 10.000 Datenpunkte und die Schwankungen folgen einer schønen Glocke. Aber so weit sind wir ja noch gar nicht.
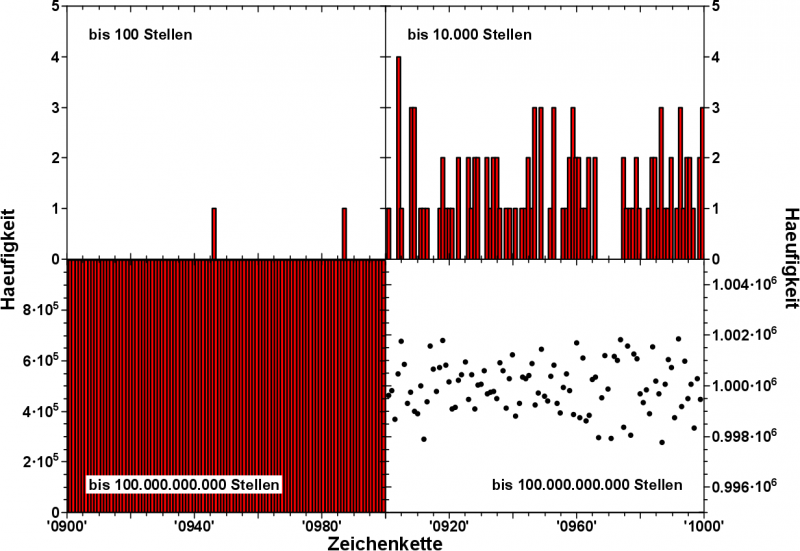
Wie sieht denn nun so eine Verteilung von 4-stelligen Zeichenketten aus. Im folgenden Bild stelle ich dies beispielhaft dar, fuer Fibonaccifolgenlaengen von 100, 10.000 und 1010 Zeichen.
Hier gezeigt ist die Entwicklung der Haeufigkeiten der Zeichenketten von „0900“ bis „1000“.
Bei einer Fibonaccifolgenlaenge von nur 100 Zeichen, kommen auch nur ca. 100 vierstellige Zeichenketten vor. Also im Durchschnitt kommt jede von den 10.000 vierstelligen Zeichenketten 0.01 mal vor. Dies zeigt die linke obere Verteilung sehr deutlich.
Bei einer Fibonaccifolgenlaenge von 10.000 Zeichen, kommt jede vierstellige Zeichenkette im Schnitt genau ein Mal vor. Dies bestaetigt die rechte obere Verteilung.
Hier spielt uns die menschliche Wahrnehmung aber einen Streich. Es scheint, als ob Haeufigkeiten von 2, 3 und gar 4, mal deutlich die Zahl der „Nullvorkommen“ ueberwiegen. Dem ist aber nicht so. Manuelles Nachzaehlen ergab, dass alle Haeufigkeiten die ueber eins liegen, die „Leerstellen“ ziemlich genau „auffuellen“, so dass im Durchschnitt eine Haeufigkeit von eins heraus kommt. So wie erwartet.
Bei einer Fibonaccifolgenlaenge von 1010 Zeichen ist die Erwartung, dass jede vierstellige Zeichenkette durchschnittlich eine Million mal auftritt. Dies sieht man in der linken unteren Verteilung bestaetigt. Im Balkendiagramm von 0 bis 1.000.000 gehen die Feinheiten aber unter. Deswegen ist unten rechts der Bereich der Verteilung um den Wert „1.000.000“ aufgespreizt zu sehen.
Und hier beginnt es interessant zu werden.
Dieses Zappeln um den Mittelwert ist ja das eigentliche Ziel meiner Fragestellung. Ist das normalverteilt?
Wie haeufig eine bestimmte Zahlenfolge vorkommt, ist also ueberhaupt nicht von Interesse. Aber wie sich die Haeufigkeit eben dieser Zahlenfolge von den Haeufigkeiten aller anderen Zahlenfolgen unterscheidet, DAS ist das Interessante. … Das Zappeln um den Mittelwert halt.
Ich kønnte hier gleich das Ergebnis praesentieren. Das waere aber langweilig.
Zunaechst einmal schauen wir uns das Zappeln und die Entwicklung des Zappelns ein bisschen naeher an.
Zur Analyse ist es unpraktisch, sich die Rohdaten anzuschauen. Da erhaelt man keine wesentlichen Informationen, denn ich habe ja prinzipiell 10.000 verschiedene Haeufigkeiten. Nun ist meine Vermutung aber, dass es deutlich wahrscheinlicher ist, dass das Vorkommen einer Zeichenkette um den Mittelwert liegt, als fern ab davon. Um dies besser zu „sehen“, erstellte ich fuer jede Potenz der Fibonaccifolgenlaenge ein Histogramm der Haeufigkeiten vierstelliger Zeichenketten. Bei diesen Histogrammen „mittelte“ ich derart, dass ich 100, gleich weite Balken hatte. Dieses Histogramm sollte dann natuerlich einer Normalverteilug entsprechen. Dazu aber an anderer Stelle mehr.
Es gibt die folgenden interessanten Grøszen:
– maximales und minimales Vorkommen;
– die Differenz daraus ergibt die Fehlerspanne;
– „DeltaMinus“ und „DeltaPlus“, der maximale Betrag der Abweichung vom Vorkommensmittelwert nach unten bzw. nach oben;
– eine Groesze die ich „relativer Fehler“ nenne: Quotient aus Fehlerspanne und Mittelwert.
Dies alles natuerlich in Abhaengigkeit von der Laenge der Fibonaccifolge.
Maximales und minimales Vorkommen sind nur in so fern von Interesse weil sich daraus andere Daten ergeben.
„Delta Minus“ und „Delta Plus“ haben eigentlich keine Bedeutung. Aber ich wollte gern mal wissen, ob die Abweichung nach oben tendentiell grøszer ist, als die nach unten (oder umgekehrt).
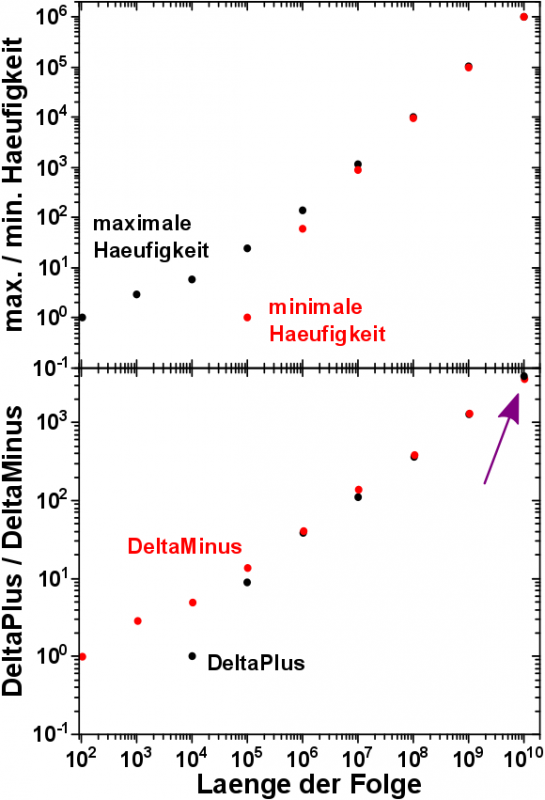
Bis zu einer Fibonaccifolgelaenge von 10.000 Stellen war das minimale Vorkommen immer null. Natuerlich gab es Zeichenketten, die ueberhaupt nicht aufgetaucht sind, wenn es nur so wenige potentielle Zeichenketten ueberhaupt gab.
Das maximale/minimale Vorkommen nimmt, wie zu erwarten war, exponentiell zu, nachdem die Fibonaccifolge eine Mindestlaenge von 10.000 Zeichen ueberrschritten hat.
Der Betrag des maximalen Abstands vom Vorkommensmittelwert nach unten (DeltaMinus, rote Punkte im unteren Grafen) ist zunaechst immer grøszer als der Abstand nach oben (DeltaPlus, schwarze Punkte im unteren Grafen). Erst im ganz letzten Messwert kommt es zu einem Umschlag dieses Verhaltens. Erwarten wuerde ich, dass es hierbei keine Praeferenz gibt. So weit scheinen die Daten allerdings Letzteres zu suggerieren. Mehr Daten sind vonnøten und ein strenger mathematischer Beweis dieser Behauptung.
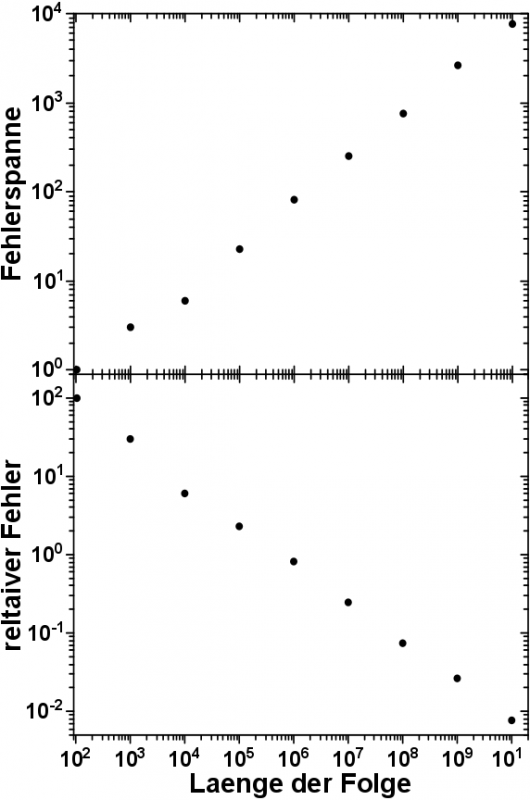
Die Fehlerspanne nimmt exponentiell zu. Der Abstand zwischen der Zeichenkette die am seltensten vorkommt und derjenigen, die am haeufigsten vorkommt, wird also absolut gesehen immer grøszer.
Auch dies ist so zu erwarten gewesen, kann sich das Vorkommen aller Zeichenketten bei laengeren Fibonaccifolgen doch ueber grøszere Bereiche „ausdehnen“.
Deswegen fuehre ich den „relativen Fehler“ ein. Auch wenn die Fehlerspanne immer grøszer wird, so wuerde ich erwarten, dass diese Fehlerspanne bezogen auf den Mittelwert des Vorkommens aller Zahlen abnehmen sollte. Die Haeufigkeiten sollten sich also relativ gesehen mehr und mehr an den Erwartungswert „anschmiegen“.
Diese Vermutung kommt _mir_ total natuerlich vor, weil ich eine Normalverteilung aller Zeichenketten annehme. Wenn ich aber mal so drueber nachdenke, dann beruht diese Annahme nur auf so ’nem „Bauchgefuehl“. Und wenn ich so weiter drueber nachdenke, dann werde ich mir unsicher, ob nicht selbst bei einer Normalverteilung der Werte, der relative Fehler immer grøszer werden kønnte … wenn also die Fehlerspanne schneller zu nimmt, als der Mittelwert grøszer wird … nein … mich duenkt, bei einer Normalverteilung kann dem nicht so sein. Aber eine Begruendung muss ich schuldig bleiben. Jedenfalls ist fest zu halten, im Allgemeinen kønnte der relative Fehler auch gleich bleiben, oder sogar zu nehmen. Wenn dem aber so waere, dann waere vermutlich die Annahme einer Normalverteilung falsch.
Jedenfalls ist in der Abbildung gut zu erkennen, dass meine Vermutung richtig war und im Umkehrschluss mglw. auch die Annahme der Normalverteilung. Dazu aber nicht mehr in diesem Beitrag. Auf dieses wunderschøne Ergebniss muesst ihr, meine lieben Leserinnen und Leser, euch bis zum naechsten Mal gedulden.
Zum Abschluss des Beitrages noch das Folgende.
ACHTUNG! Die Definition „_meines_ relativen Fehlers“ hat nichts mit dem relativen Fehler zu tun, wie er vom Studium und aus der Mathematik her bekannt sein sollte. Dieser wird naemlich bspw. fuer einzelne Messwerte angegeben, als (relative) Abweichung vom wahren Wert. Hier habe ich aber ein Ensemble von Messwerten und betrachte die Gesamtheit.