Eigentlich interessiert mich ja nicht die Haeufigkeit einer bestimmten Zeichenkette. Wirklich von Interesse ist die Streuung der Haeufigkeiten der Zeichenketten.
Oder einfacher (aber mit mehr Worten) erklaert: wenn bspw. die Zeichenkette „1234“ fuenf Mal vor kommt, so møchte ich wissen, wie viele Zeichenkette auch fuenf mal vorkomen. Dabei interessiert es mich nicht die Bohne, welche Zeichenketten das sind.
Bestimmte Zahlen weisen eine gewisse Haeufigkeit auf und mich interessiert es, wie oft diese Haeufigkeit auftritt. Hier vermute ich die Normalverteilung.
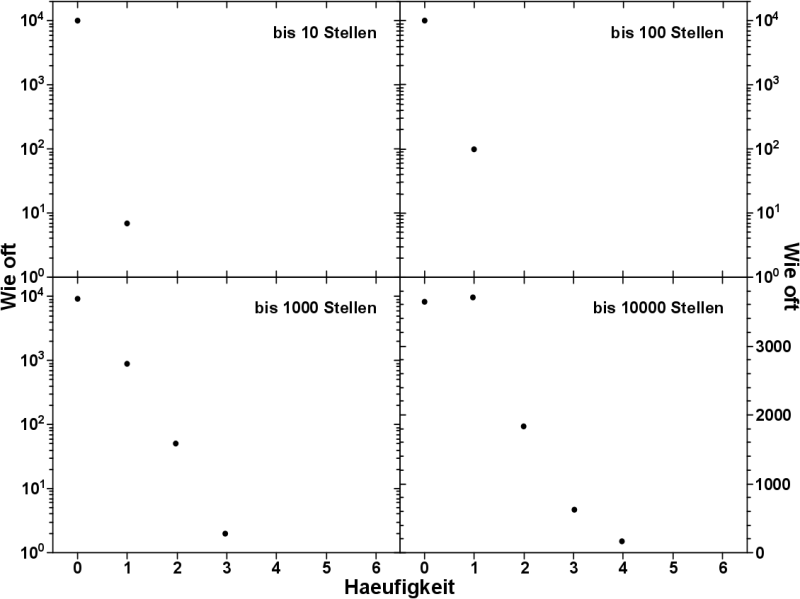
Aber schauen wir uns doch konkrete Daten, fuer vierstellige Zeichenketten, an:
So lange die Anzahl der Stellen in der Folge nicht ausreicht, damit jede Zahl mehr als ein Mal auftreten kønnte, ist natuerlich keine glockenførmige Verteilung zu erkennen. Dies sieht man in diesen vier Grafen.
Wenn die Folge nur 10 Zeichen lang ist, so kommen ca. 10.000 vierstellige Zeichenketten genau null Mal vor. Und ein paar wenige ein Mal.
Je laenger die Folge wird, desto mehr Zeichenketten kønnen ein Mal vorkommen (bis 100 Stellen) und irgendwann auch øfter als ein Mal (bis 1000 Stellen). Allerdings nimmt das Vorkommen høherer Haeufigkeiten exponentiell ab. Was zu erwarten war.
Ab einer Folgenlaenge von 10.000 Zeichen, kommt im Schnitt jedes Zeichen genau ein Mal vor. Das hatte ich ja bereits letztes Mal gezeigt.
Man beachte, dass die Ordinate nun linear ist!
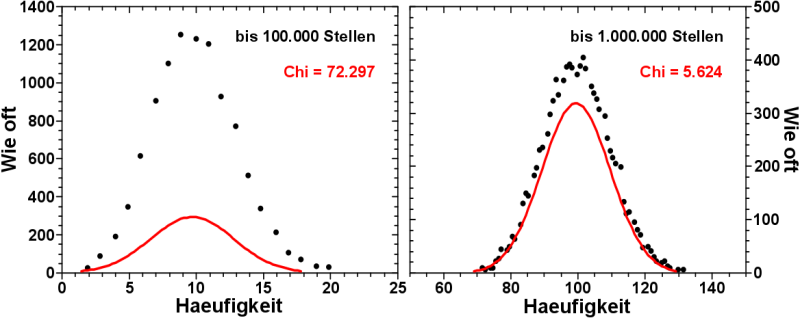
Und wenn die Folge weiter waechst, so stellt sich auch eine glockenførmige Verteilung ein:
Aber HAEH?! Wieso liegt denn die schicke rote Kurve (vulgo: der Fit) nicht auf den Datenpunkten? Und was ist dieses komische „Chi“?
Dies liegt daran, weil diese schøne rote Kurve den Daten angepasst wurde, unter der Annahme, dass diese normalverteilt sind. Und hier kommt Chi ins Spiel. Chi ist ein Ausdruck fuer die Guete des Fits. Je høher dieser Wert, desto schlechter stimmen die Daten mit der Annahme ueberein.
Oder andersherum: das Datenauswertungsprogramm passt die Parameter der Kurve derart an, dass Chi so gering wie møglich wird. Nicht, dass es am Schønsten aus sieht.
Demnach kønnte man sagen, dass bis zu einer Folgenlaenge von 100.000 Stellen fuer vierstellige Zeichenketten NICHT normalverteilt ist.
Aber wie das rechte Bild zeigt, so scheint sich sich die Verteilung einer Normalverteilung anzunaehern, mit zunehmender Folgenlaenge.
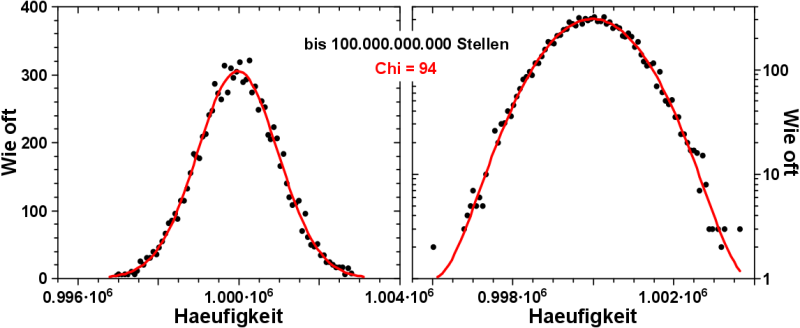
Und hier nun, ENDLICH, kommt das, worauf ihr, meine lieben Leserinnen und Leser, so lange warten musstet:
Bei einer Fibonaccifolgenlaenge von 100.000.000.000 Stellen, meine ich, dass man durchaus davon sprechen kann, dass vierstellige Zeichenketten normalverteilt sind. Toll wa!
Dies gilt insb. auch fuer kleine Vorkommen, was die logarithmische Darstellung im rechten Bild eindrucksvoll zeigt.
Damit hatte ich endlich herausgefunden, was ich herausfinden wollte. Natuerlich nur innerhalb meines eigenen, mathematisch nicht so anspruchsvollen Rahmens.
Und ihr, meine lieben Leser und Leserinnen, wisst es nun auch.
Leave a Reply