Søren in Norwegen

Wie im vorhergehenden Beitrag dieser Reihe beschrieben, braucht mein erster Ansatz, den Computer einfach erstmal die Folge ausrechnen und danach analysieren zu lassen, unheimlich viel Arbeitsspeicher.

Also musste ein neuer Plan her.

Fancypancy meinte ein studierter Experte, dass ich um „streaming“ wohl nicht drumherum komme. Das war dann auch das, was ich mir vorher schon dachte. Anstatt die ganze Folge zu erstellen, lass ich nur jeweils ein (neues) Element nach dem anderen analysieren, bevor das naechste Element erstellt wird.
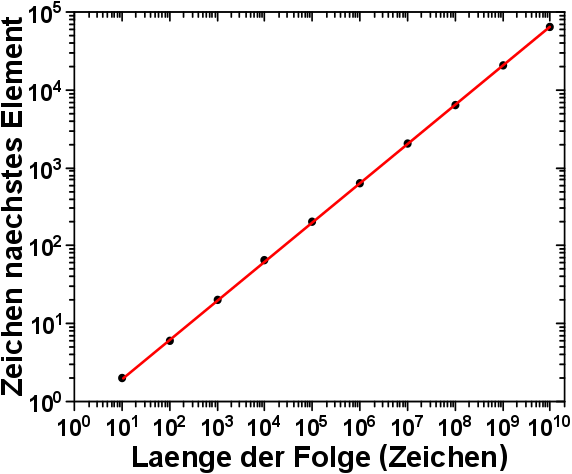
Das sollte natuerlich deutlich weniger Speicher benøtigen. Wie viel weniger, ist hier zu sehen:

Selbstverstaendlich verhaelt sich die Laenge des naechsten hinzuzufuegenden Elementes nach dem gleichen Gesetz wie die Laenge der gesamten Folge – exponentiell. Aber wenn man die Skala der Ordinate mit der in der Abbildung im oben verlinkten, vorhergehenden Beitrag vergleicht, so sieht man doch wie, absolut gesehen, gewaltig weniger die Laenge des naechsten Elementes im Vergleich zur Laenge der gesamten Folge waechst.
Wenn man den (maximalen) Speicherbedarf betrachtet, so muesste man die Anzahl der Zeichen des als naechstes hinzuzufuegenden Elementes verdreifachen. Dies deswegen, da ich ja immer zwei Elemente im Speicher behalten muss, um das neue (dritte) Element auszurechnen. Daher der Faktor drei. Aber ein Faktor drei … bei exponentiellem Wachstum … tihihi … ich lach mich kaputt … da spricht man nicht drueber ;)

Das (wenn auch exponentielle) Wachstum des naechsten hinzuzufuegenden Elementes geht also deutlich weniger schnell von statten, als das Wachstum der Laenge der gesamten Folge.

Damit war mein Plan zu „streamen“ auf ein solides Fundament gestellt.

Der Analyseteil blieb im Wesentlichen der Gleiche: so viele Zeichen abhacken wie benøtigt, die Haeufigkeit dieser Zahl um eins erhøhen, in der Folge um eins nach rechts ruecken, von vorne beginnen.

Das bedeutete aber nicht, dass es jetzt einfacher war. Ganz im Gegenteil. Ich musste viel mehr ueberlegen um den „streaming“-Teil richtig hin zu bekommen.

Natuerlich war es einfach das naechste Element erst dann auszurechnen und zu analysieren, wenn es benøtigt wird. Dabei muessen aber drei Sachen beachtet werden.
1.: Man benøtigt einen „Ueberhang“ der letzten Zahlen aus dem vorherigen Element.
2.: Aufpassen, dass beim „Ueberhang“ zaehlen nicht doppelt gezaehlt wird.
3.: Was ist, wenn das naechste anzuhaengende Element weniger Zeichen hat, als die Laenge der zu untersuchenden Zeichenketten.

Eine Veranschaulichung zu 1.
Wir nehmen die Zeichenkette 112 und uns interessieren nur ein- und zweistellige Zeichenketten. Dann haben wir darin folgende Verteilung: „1“ = 2 mal, „2“ = 1 mal, „11“ = 1 mal und „12“ = 1 mal
Das naechste Element ware die 3. Wenn wir NUR dieses betrachten wuerden, so wuerden zur obigen Verteilung hinzukommen: „3“ = 1 mal.
Wenn ich aber an die Zeichenkette 112 die 3 anhaenge, so erhalte ich 1123 und wenn ich dies analysiere, so erhalte ich: „1“ = 2 mal, „2“ = 1 mal, „3“ = 1 mal, „11“ = 1 mal, „12“ = 1 mal (bis hierhin also wie gehabt) und zusaetzlich: „23“ = 1 mal.
Beim „Uebergang“ von der 2 zur 3 „entsteht“ eine neue 2-stellige Zahl – die 23. Und die wuerde man uebersehen, wenn man einfach nur das neue Element analysiert.

Bevor man also das neue Element analysiert, muss man an dieses so viele Zeichen vorne ran haengen, wie die Laenge der laengsten zu untersuchenden Zeichenkette ist, minus ein Zeichen. Und das ist das, was ich „Ueberhang“ nenne.

Das ist gar nicht so schwer, sich diesen Ueberhang zu merken. Bei der Analyse muss man einfach nur schauen, wenn die Laenge der von der Folge abgehackten Zahlen, das erste Mal kuerzer wird, als die Laenge der grøszten zu untersuchenden Zeichenkette.

Eine Veranschaulichung zu 2. unter Beruecksichtigung des ersten Punktes.
Wir interessieren uns fuer vier-, drei,- und zweistellige Zeichenketten. Wir nehmen an, dass bis zur 11235813 alles untersucht wurde. Der Ueberhang muesste also 813 werden und das naechste Element wird die 21. Als neue Folge erhalten wir also 81321. Nach dem im vorhergehenden Beitrag vorgestellten Algorithmus untersuche ich dann zunaechst 8132. Davon wuerde die letzte Zahl abgehackt werden um die dreistellige Zeichenkette zu analysieren – also die 813. Hier ist es nun aber so, dass die 813 schon vorher gezaehlt wurde. Bei der Untersuchung der „alten“ Zeichenkette, bevor das neue Element erzeugt wurde. So auch die 81 und die 8.
Im naechsten Schritt waere alles ok mit der 1321 und mit der 132, aber die 13 und die 1 waere auch schon vorher gezaehlt worden.

Der Analysealgorithmus muss das Hinzuaddieren zur Haeufigkeit also rechtzeitig unterbrechen, so lange der Ueberhang noch involviert ist.

Eine Veranschaulichung zu 3.
Hierbei handelt es sich eher um ein technisches, als um ein logisches Hindernis.
Zunaechst denken wir uns das gleiche wie unter 2. Das naechste hinzuzufuegende Element (die 21) ist also ein Zeichen zu kurz um keine Probleme zu bereiten, wenn mich vierstellige Zeichenketten interessieren. Zunaechst ist alles ok. Aus 81321 mache erstmal 8132 und analysiere das. Dann folgt 1321 und dies wird untersucht.
Dann aber ist tritt bei der Umwandlung einer Zeichenkette zu einer Zahl etwas auf, was Probleme bereitet.
Die naechste Zeichenkette waere die 321, also nur noch drei Zeichen lang. Hierbei wuerde der von mir gewaehlte Algorithmus zunaechst annehmen, dass das vierte „Zeichen“ sozusagen „unsichtbar“ ist. Es wuerde also die Zeichenkette „321( )“ umgewandelt werden in … richtig … 321. Danach wuerde das letzte (unsichtbare) Element abgehackt werden und die 321 wuerde nochmal gezaehlt.

So ein Mist aber auch! Nun ja, ich konnte ich auch dieses Problem løsen. Drittens ist vor allem ein Anfangsproblem. Das taucht nicht mehr auf, sobald die neuen Elemente lang genug werden. Dennoch muss es waehrend der ersten Durchlaeufe natuerlich durch eine gut gewaehlte Abbruchbedingung beruecksichtigt werden. Zweitens ist zwar ein permanentes Problem, aber auch hier schafft eine passende Abbruchbedingung das daraus folgende doppelte Zaehlen aus der Welt. Und Erstens ist easy peasy zu bewerkstelligen.

Wie gesagt: dumme Computer! Machen genau das, was man ihnen sagt und nicht das, was man eigentlich møchte, was sie machen sollen.

Letztlich lagerte ich die Analyse des Ueberhangproblems in einen eigenen kleinen Algorithmus aus, der vor der eigentlichen Analyse des neuen Elementes ablaeuft.

Warum schreibe ich das alles … mhm … weil es ja mglw. wen interessiert und dieser weblog auch ein bisschen meiner eigenen Dokumentation dient :)

Falls es jemanden interssiert, so wuerde ich mit Freude den in Python geschriebenen Quellcode des von mir erstellten Programms teilen.
Insb. auch, weil ich hoffe Anregungen zu bekommen.
Es ist immer lehrreich An- und Bemerkungen von auszerhalb des eigenen Kosmos zu erhalten.

In den naechsten Beitraegen werde ich dann endlich die mithilfe dieses Programmes gewonnen Daten (oder vielmehr deren weitergehende Analyse) vorstellen.
Das war ja schlieszlich der eigentliche Grund, warum ich mir diesen ganzen Aufwand gemacht habe.
Das erste Ergebnis ist im Uebrigen schon hier (oben) zu sehen. Ich musste ja schlieszlich erstmal das Element mit 64.651 Stellen (und alle davor) ausrechnen, um euch diesen schønen Zusammenhang zeigen zu kønnen.