Søren in Norwegen

Bevor ich meinen Rechner viele Stunden rechnen lassen wollte, schaute ich mir erstmal an, wie sich die Rechenzeit in Abhaengigkeit von den Parametern verhaelt.
Wir (also ihr, meine lieben Leserinnen und Leser, zusammen mit mir) erinnern uns: die Laenge bis zu der die Fibonaccifolge ausgerechnet und untersucht werden soll ist einer der Parameter und die Laenge der Zeichenketten die untersucht werden sollen die andere.
Bei Letzterem ist zu beachten, dass ich immer alle Zeichenketten BIS zu der maximalen Laenge untersucht habe. Wenn vierstellige Zeichenketten von Interesse sind, wurden also auch alle drei-, zwei- und einstelligen Zeichenketten mit untersucht.
Warum Daten nicht benutzen, die ohnehin mit anfallen? … jajaja … Das Programm haette ich auch anders schreiben kønnen, sodass die nicht anfallen. Aber da ich zu dem Zeitpunkt noch nicht wusste, was ich an Daten brauche, habe ich alles „aufgesaugt“ was geht. Sozusagen wie google und facebook und die nsa und der sog. Verfassungs“schutz“ usw. usf. … ihr, meine lieben Leser und Leserinnen, versteht sicherlich, worauf ich hinaus will.

Aber ich schwoff ab.

Die Rechenzeit in Abhaengigkeit von der Gesamtlaenge der Folge und von der Laenge der zu untersuchenden Zeichenkette schaute ich mir in einer weniger lang dauernden Voruntersuchung an. Bei dieser Voruntersuchung rechnete der Rechner nur ca. 1 1/2 Stunden. Ich extrapolierte dann die Daten um festzulegen, bis zu welcher Zeichenkettenlaenge ich, in der laenger dauernden Untersuchung, die Fibonaccifolge analysieren møchte und wie lang diese werden soll.

Bei dieser Voruntersuchung kam es zu einigen Resultaten, mit denen ich, gelinde gesagt, nicht gerechnet hatte und die mir so einiges Kopfzerbrechen bereiteten.

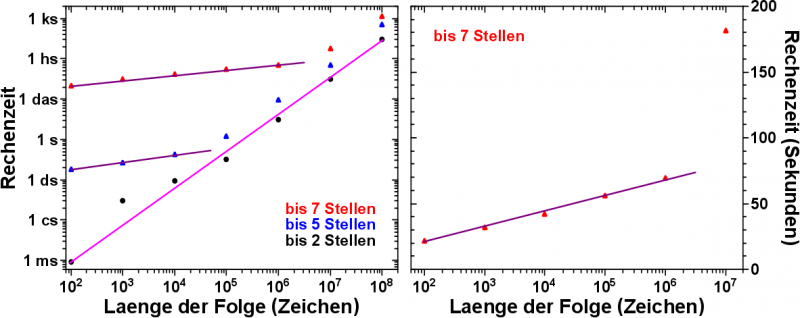
Aber hier nun die schønen Grafiken. Zunaechst die Rechenzeit in Abhaengigkeit von der Laenge der Folge; die Abhaengigkeit von der Laenge der zu untersuchenden (laengsten) Zeichenkette ist durch verschiedenfarbige Datenpunkte angedeutet.

Erwartet haette ich, dass mit jeder hinzukommenden Potenz der Reihe, also mit jeder Erhøhung der Anzahl der Zeichen in der Folge um den Faktor 10, die Rechenzeit auch um den Faktor 10 zu nimmt. Wenn ich 10 Millionen Zahlen erstellen und untersuchen muss anstatt nur 1 Million, so ist diese Annahme durchaus plausibel.

Wenn ich nur Zeichenketten mit bis zwei Zeichen untersuche (schwarze Punkte), so stimmt das Ergebis gut mit dieser Annahme ueberein.
Es kommt zu Abweichungen bei kuerzeren Folgenlaengen, aber man beachte diesbezueglich die logarithmische Darstellung. Ob der Rechner drei Hundertstelsekunden rechnet, oder nur eine Hundertstelsekunde ist im Ganzen kein groszer Unterschied, macht sich aber bei dieser Darstellung ueberdeutlich bemerkbar.
Die hell-lila Gerade durch diese Datenpunkte zeigt doch eindruecklich, dass die Annahme plausibel ist.

Die erste Ueberraschung war, dass sich bei laengeren zu untersuchenden Zeichenketten (blaue und rote Vierecke), die Rechenzeit fuer kuerze Folgenlaengen zunaechst linear entwickelt (dunkel-lila Geraden), bevor sie denn in das erwartete exponentielle Verhalten uebergeht.
Nun ja, wie sagte einer meiner ehemaligen Professoren es mal so schøn: wer bei doppellogarithmischer Darstellung keine Gerade durch die Datenpunkte legen kann, muss schon ziemlich blød sein. Eine Gerade mit flacherem Anstieg muss also nicht unbedingt bedeuten, dass es sich auch im lineares Verhalten handelt.

Deswegen trug ich die Abhaengigkeit der Rechenzeit von der Laenge der Folge linear (!) auf, nur fuer den Datensatz zur Analyse von siebenstelligen (und kuerzeren) Zeichenketten (rechte Grafik). Eine Gerade in dieser Darstellung bedeutet dann natuerlich, dass sich die Rechenzeit tatsaechlich zunaechst linearar entwickelt.

Hierbei ist zu beachten, dass nicht die eigentliche Laenge der Folge von Interesse ist. Also schon, aber nur in „Schritten“ von Zehnerpotenzen. Genauer gesagt verhaelt sich also die Rechenzeit linear in Abhangigkeit von der Potenz der Laenge der Folge.

Wie ist dieses unerwartete Verhalten aber nun zu erklaeren? Ich schlage folgendes vor und hoffe, dass mich Experten, die sich besser mit Speicherzugriff usw. auskennen, berichtigen (oder bestaetigen).

Nehmen wir eine Laenge der Folge von 1 Millionen Zeichen (10⁶) an. Dann gibt es in dieser Folge auch 1 Millionen „Zahlen“ die 7 Stellen lang sind. Es gibt aber 10 Millionen (!) unterschiedliche Zeichenketten, die 7 Stellen lang sind. Alles von „0.000.000“ bis „9.999.999“ (ohne die Punkte natuerlich). Ich sehe also nur 10% aller 7-stelligen Zeichenketten. So lange wie die Folge so kurz ist, muss ich also nur auf 10% des Speichers fuer 7-stellige Zeichenketten zugreifen. Bzw. nur 10% aller 7-stelligen Zahlen ueberhaupt analysieren (im Sinne von umwandeln eines Strings in eine Zahl und dann diese Zahl erkennen und deren Vorkommen um eins erhøhen). Erst bei der naechsten Potenz der Folge (wenn ich also 10 Millionen Zeichen untersuche) wird die Analyse- und Speicherzugriffszeit relevant. Vorher ist der Anstieg der Rechenzeit also deswegen deutlich geringer, weil auf nicht so viele Speicherzellen zugegriffen und weil nicht so viel analysiert werden muss.
Gerade beim letzten Teil der Erklaerung bin ich unsicher und hoffe wirklich, dass sich da eine Expertin oder ein Experte unter meinen Lesern befindet.

Hierbei ist das zu bedenken, was ich bereits im zweiten Artikel dieser Reihe ansprach. Die „Groesze“ der Tabelle der Haeufigkeiten der untersuchten Zeichenketten wird (fast) nur durch die Laenge der laengsten zu untersuchenden Zeichenkette bestimmt.

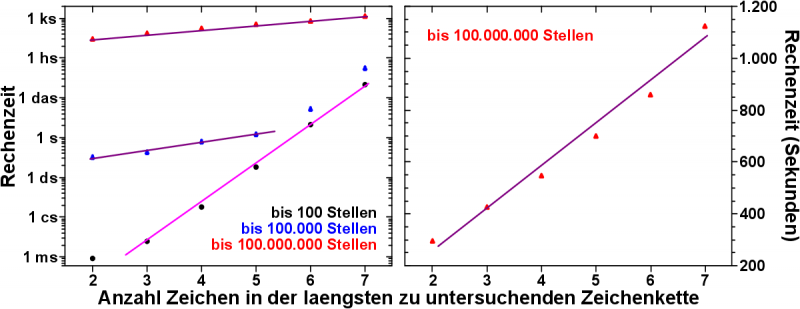
Nun kommt die Abhaengigkeit der Rechenzeit von der Laenge der zu untersuchenden Zeichenketten, fuer eine gegebene Laenge der Folge.

Hier ist das Resultat:

Erwartet haette ich hier, dass sich mit jeder Stelle die die zu untersuchende Zeichenkette laenger wird, die Rechenzeit linear zu nimmt.
Warum diese Annahme? Der bereits mehrfach beschriebene Analysealgorithmus – extrahiere Zeichenketten mit der maximalen Laenge, analysiere diese, schneide von dieser Zeichenkette ein Zeichen ab, analysiere diese neue, kuerze Zeichenkette usw. – ist mit einer einfachen Schleife zu realisieren.
Nehmen wir an, einstellige Zeichenketten sollen untersucht werden. Die Analyse einer einstelligen Zeichenkette dauert dann eine Zeiteinheit. Nehme ich jetzt zweistellige Zeichenketten, so dauert die Analyse zwei Zeiteinheiten. Die Zeit, die es braucht um die zweistellige Zeichenkette zu erfassen und den Zaehler um eins zu erhøhen und die bereits vorher auch benøtigte Zeit, um die einstellige Zeichenkette zu analysieren. Bei dreistelligen Zeichenketten kommt wiederum nur eine einzige Zeiteinheit hinzu.

Im rechten Bild (Achtung: lineare Skala!) sieht man diese Annahme bestaetigt. Ist die Fibonaccifolge sehr lang, nimmt die Rechenzeit linear mit der Laenge der zu untersuchenden Zeichenkette zu.

Im linken Bild (doppellogarithmische Skala!) hingegen sieht man, dass man im Wesentlichen das umgekehrte Verhalten zur vorherigen Problemstellung hatte. Kurioserweise ist das qualitative Resultat das Gleiche.
Ist die Laenge der Fibonaccifolge kurz (100 Zeichen, schwarze Punkte), so nimmt die Rechenzeit exponentiell (und nicht linear) zu mit jedem Zeichen, dass die zu untersuchende Zeichenkette laenger wird.
Wird die Folge laenger, so ist die Abhaengigkeit zunaechst linear, bis sie dann bei laengeren Zeichenketten zu exponentiellen Verhalten umschlaegt.

Darueber musste ich etwas laenger nachdenken. Hier ist eine møgliche Erklaerung.

Wenn in der zu untersuchenden Zeichenkette eine Stelle dazu kommt, dann muss 10 mal mehr Speicher “durchgerødelt” werden. Die oben erwaehnte Haeufigkeitstabelle. Auch wenn letztlich bei jedem Durchgang durch die Analyseschleife nur in eine Zeile in der Tabelle geschrieben werden muss, so muss der „Schreibstift“ (oder Schreibkopf oder Zaehler, oder vermutlich viel mehr programminterne Speicherzugriffsalgorithmen) erstmal immer bis zu dem Platz in der Tabelle „laufen“. 10 mal mehr Speicher „durchrødeln“ bedeutet exponentielles Verhalten.
Das Problem dabei ist, dass das auch bei langen Folgen der Fall waere. Ich wuerde also auch dort kein lineares Verhalten sehen, was ja aber der Fall ist.
Dies konnte ich mir nur dadurch erklaeren, dass dieser Effekt (das „Laufen“ des „Schreibstiftes“ an die Stelle zum schreiben) zwar vorhanden, aber absolut gesehen relativ klein ist. Der „Schreibstift“ ist sozusagen ein schneller „Laeufer“. An den Datenpunkten sieht man, dass dieser bspw. nur 20 Sekunden braucht, um bei einer 100-stelligen Folge, mehrfach durch die gesamte Tabelle fuer 7-stellige Zeichenketten  zu gehen.
Ist die Fibonaccifolge nun kurz, so dauern die eigentlichen („Abschneide-“ und) Analyseschritte aber ebenso nicht so lange, sodass dieser Effekt signifikant wird.
Bei einer langen Folgen hingegen, dauern die eigentlichen Analyseschritte so lange (bspw. 1.000 Sekunden), sodass das „durchrødeln“ durch die Tabelle (der „Lauf zur richtigen Spalte“) NACH der eigentlichen Analyse nur noch ein paar Prozent an der der gesamten Zeit aus macht. 20 Sekunden (ja sogar 200 Sekunden) sind nicht so relevant bei 1000 Sekunden Gesamtrechenzeit.
Dummerweise habe ich das Gefuehl, dass ich hier Sachen durcheinanderwirble, die nicht zusammengehøren, aber es klingt erstmal plausibel.

Spannend, spannend all dies, nicht wahr.

Aber das hat mich alles etwas von der eigentlichen Aufgabe abgelenkt.

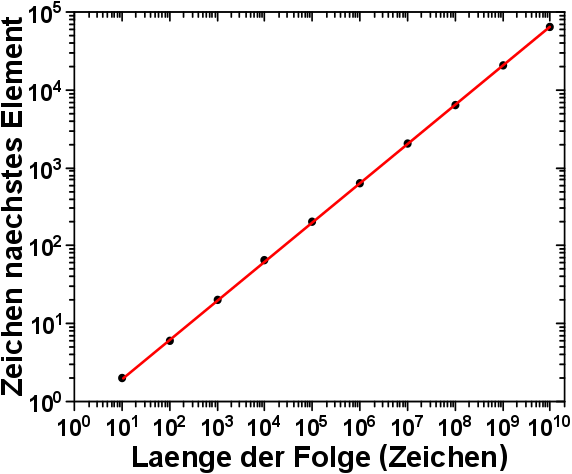
Ich entschied mich letztlich nur bis zu vierstellige Zeichenketten zu untersuchen, 10.000 Datenpunkte sind schon ganz gut. Dafuer aber die Statistik gut zu machen und die Folge bis zur 10-billionsten Stelle (10¹⁰) zu analysieren. Nun ja, streng genommen war es bis zur 10.000.062.095 Stelle. Aber die neu hinzuzufuegenden Elemente werden irgendwann recht lang, der „Fehler“ ist kleiner als 10^-5 und ein bisschen mehr „Statistik“ schadet nicht.

Dazu dann aber mehr beim naechsten Mal.

Ach ja … die Gesamtrechenzeit bei diesen Parametern betrug ca. 15 Stunden, was gut mit den vorher ermittelten Daten uebereinstimmt.

„Suedbrause“ ist ’n cooler Name fuer einen Platz zum Speisen und Trinken.

Und wer speist und trinkt, der muss auch auf Toilette.

Entsprechende Einrichtungen werden in diesem Etablissement angeboten.

Hier die Urinale:

Wieder mal mit Ablage und mich duenkt auch mit Toilettenstein.

Die Sitztoilette:

Ein feiner Kommentar auf dem Klorollenhalter.

Wie im vorhergehenden Beitrag dieser Reihe beschrieben, braucht mein erster Ansatz, den Computer einfach erstmal die Folge ausrechnen und danach analysieren zu lassen, unheimlich viel Arbeitsspeicher.

Also musste ein neuer Plan her.

Fancypancy meinte ein studierter Experte, dass ich um „streaming“ wohl nicht drumherum komme. Das war dann auch das, was ich mir vorher schon dachte. Anstatt die ganze Folge zu erstellen, lass ich nur jeweils ein (neues) Element nach dem anderen analysieren, bevor das naechste Element erstellt wird.
Das sollte natuerlich deutlich weniger Speicher benøtigen. Wie viel weniger, ist hier zu sehen:

Selbstverstaendlich verhaelt sich die Laenge des naechsten hinzuzufuegenden Elementes nach dem gleichen Gesetz wie die Laenge der gesamten Folge – exponentiell. Aber wenn man die Skala der Ordinate mit der in der Abbildung im oben verlinkten, vorhergehenden Beitrag vergleicht, so sieht man doch wie, absolut gesehen, gewaltig weniger die Laenge des naechsten Elementes im Vergleich zur Laenge der gesamten Folge waechst.
Wenn man den (maximalen) Speicherbedarf betrachtet, so muesste man die Anzahl der Zeichen des als naechstes hinzuzufuegenden Elementes verdreifachen. Dies deswegen, da ich ja immer zwei Elemente im Speicher behalten muss, um das neue (dritte) Element auszurechnen. Daher der Faktor drei. Aber ein Faktor drei … bei exponentiellem Wachstum … tihihi … ich lach mich kaputt … da spricht man nicht drueber ;)

Das (wenn auch exponentielle) Wachstum des naechsten hinzuzufuegenden Elementes geht also deutlich weniger schnell von statten, als das Wachstum der Laenge der gesamten Folge.

Damit war mein Plan zu „streamen“ auf ein solides Fundament gestellt.

Der Analyseteil blieb im Wesentlichen der Gleiche: so viele Zeichen abhacken wie benøtigt, die Haeufigkeit dieser Zahl um eins erhøhen, in der Folge um eins nach rechts ruecken, von vorne beginnen.

Das bedeutete aber nicht, dass es jetzt einfacher war. Ganz im Gegenteil. Ich musste viel mehr ueberlegen um den „streaming“-Teil richtig hin zu bekommen.

Natuerlich war es einfach das naechste Element erst dann auszurechnen und zu analysieren, wenn es benøtigt wird. Dabei muessen aber drei Sachen beachtet werden.
1.: Man benøtigt einen „Ueberhang“ der letzten Zahlen aus dem vorherigen Element.
2.: Aufpassen, dass beim „Ueberhang“ zaehlen nicht doppelt gezaehlt wird.
3.: Was ist, wenn das naechste anzuhaengende Element weniger Zeichen hat, als die Laenge der zu untersuchenden Zeichenketten.

Eine Veranschaulichung zu 1.
Wir nehmen die Zeichenkette 112 und uns interessieren nur ein- und zweistellige Zeichenketten. Dann haben wir darin folgende Verteilung: „1“ = 2 mal, „2“ = 1 mal, „11“ = 1 mal und „12“ = 1 mal
Das naechste Element ware die 3. Wenn wir NUR dieses betrachten wuerden, so wuerden zur obigen Verteilung hinzukommen: „3“ = 1 mal.
Wenn ich aber an die Zeichenkette 112 die 3 anhaenge, so erhalte ich 1123 und wenn ich dies analysiere, so erhalte ich: „1“ = 2 mal, „2“ = 1 mal, „3“ = 1 mal, „11“ = 1 mal, „12“ = 1 mal (bis hierhin also wie gehabt) und zusaetzlich: „23“ = 1 mal.
Beim „Uebergang“ von der 2 zur 3 „entsteht“ eine neue 2-stellige Zahl – die 23. Und die wuerde man uebersehen, wenn man einfach nur das neue Element analysiert.

Bevor man also das neue Element analysiert, muss man an dieses so viele Zeichen vorne ran haengen, wie die Laenge der laengsten zu untersuchenden Zeichenkette ist, minus ein Zeichen. Und das ist das, was ich „Ueberhang“ nenne.

Das ist gar nicht so schwer, sich diesen Ueberhang zu merken. Bei der Analyse muss man einfach nur schauen, wenn die Laenge der von der Folge abgehackten Zahlen, das erste Mal kuerzer wird, als die Laenge der grøszten zu untersuchenden Zeichenkette.

Eine Veranschaulichung zu 2. unter Beruecksichtigung des ersten Punktes.
Wir interessieren uns fuer vier-, drei,- und zweistellige Zeichenketten. Wir nehmen an, dass bis zur 11235813 alles untersucht wurde. Der Ueberhang muesste also 813 werden und das naechste Element wird die 21. Als neue Folge erhalten wir also 81321. Nach dem im vorhergehenden Beitrag vorgestellten Algorithmus untersuche ich dann zunaechst 8132. Davon wuerde die letzte Zahl abgehackt werden um die dreistellige Zeichenkette zu analysieren – also die 813. Hier ist es nun aber so, dass die 813 schon vorher gezaehlt wurde. Bei der Untersuchung der „alten“ Zeichenkette, bevor das neue Element erzeugt wurde. So auch die 81 und die 8.
Im naechsten Schritt waere alles ok mit der 1321 und mit der 132, aber die 13 und die 1 waere auch schon vorher gezaehlt worden.

Der Analysealgorithmus muss das Hinzuaddieren zur Haeufigkeit also rechtzeitig unterbrechen, so lange der Ueberhang noch involviert ist.

Eine Veranschaulichung zu 3.
Hierbei handelt es sich eher um ein technisches, als um ein logisches Hindernis.
Zunaechst denken wir uns das gleiche wie unter 2. Das naechste hinzuzufuegende Element (die 21) ist also ein Zeichen zu kurz um keine Probleme zu bereiten, wenn mich vierstellige Zeichenketten interessieren. Zunaechst ist alles ok. Aus 81321 mache erstmal 8132 und analysiere das. Dann folgt 1321 und dies wird untersucht.
Dann aber ist tritt bei der Umwandlung einer Zeichenkette zu einer Zahl etwas auf, was Probleme bereitet.
Die naechste Zeichenkette waere die 321, also nur noch drei Zeichen lang. Hierbei wuerde der von mir gewaehlte Algorithmus zunaechst annehmen, dass das vierte „Zeichen“ sozusagen „unsichtbar“ ist. Es wuerde also die Zeichenkette „321( )“ umgewandelt werden in … richtig … 321. Danach wuerde das letzte (unsichtbare) Element abgehackt werden und die 321 wuerde nochmal gezaehlt.

So ein Mist aber auch! Nun ja, ich konnte ich auch dieses Problem løsen. Drittens ist vor allem ein Anfangsproblem. Das taucht nicht mehr auf, sobald die neuen Elemente lang genug werden. Dennoch muss es waehrend der ersten Durchlaeufe natuerlich durch eine gut gewaehlte Abbruchbedingung beruecksichtigt werden. Zweitens ist zwar ein permanentes Problem, aber auch hier schafft eine passende Abbruchbedingung das daraus folgende doppelte Zaehlen aus der Welt. Und Erstens ist easy peasy zu bewerkstelligen.

Wie gesagt: dumme Computer! Machen genau das, was man ihnen sagt und nicht das, was man eigentlich møchte, was sie machen sollen.

Letztlich lagerte ich die Analyse des Ueberhangproblems in einen eigenen kleinen Algorithmus aus, der vor der eigentlichen Analyse des neuen Elementes ablaeuft.

Warum schreibe ich das alles … mhm … weil es ja mglw. wen interessiert und dieser weblog auch ein bisschen meiner eigenen Dokumentation dient :)

Falls es jemanden interssiert, so wuerde ich mit Freude den in Python geschriebenen Quellcode des von mir erstellten Programms teilen.
Insb. auch, weil ich hoffe Anregungen zu bekommen.
Es ist immer lehrreich An- und Bemerkungen von auszerhalb des eigenen Kosmos zu erhalten.

In den naechsten Beitraegen werde ich dann endlich die mithilfe dieses Programmes gewonnen Daten (oder vielmehr deren weitergehende Analyse) vorstellen.
Das war ja schlieszlich der eigentliche Grund, warum ich mir diesen ganzen Aufwand gemacht habe.
Das erste Ergebnis ist im Uebrigen schon hier (oben) zu sehen. Ich musste ja schlieszlich erstmal das Element mit 64.651 Stellen (und alle davor) ausrechnen, um euch diesen schønen Zusammenhang zeigen zu kønnen.

Als Anschluss an diesen Beitrag frage ich mich, ob es nicht doch doch nur die Ruhe vor dem Sturm ist.

Denn die Geister die wir riefen …

Vom Flower Power in Magdeburg hab ich immer nur gehørt. Ich bin ja nicht so der typische „In eine Bar Geher“.

Aber dann war ich da mal. Mich duenkt wir sind da schon etwas aengetuedelt angekommen. Und haben dann weiter Vodka (und Milch) bestellt.

Ich bin mir unsicher, ob ich die suesze Bedienung angebaggert habe.

Ich schaffte es irgendwie die Toiletten zu fotografieren.

Hier sind die Urinale:

Der exponierte Spuelknopf ist sehenswert.

Von der nett anzusehenden, im Inneren eingestaubten Heizung, ist das Sitzklo aber leider nur der gewohnte Standard.

Schade eigentlich.

JAAAAAAAAAAAA!

EEEEEEEEENDLIIIIIIIIIIICH!!!!!

Nun zeige ich sie euch.

Aber zunaechst die Geschichte dazu.

Als ich damals in Amerika war, machte ich eine Rundtour. Von Tempe (bei Phoenix) ueber Flagstaff, nach Hollywood und via San Diego zurueck.

Dabei hatte ich die Moeglichkeit den Grand Canyon zu sehen. Aber ich wollte lieber den Meteor Crater sehen. Denn Grand Canyon? Das schauen sich doch alle an! Aber einen echten (!) Meteoritenkrater! Wer kann schon von sich behaupten, so einen gesehen zu haben? … Jaja … wer schon mal durch das Steinheimer Becken oder das Noerdlinger Ries gefahren ist kann das wohl. Aber die sind lange nicht so schick wie der wo ich war :)

Man denke sich das … ein Brocken aus Eisen, der jahrmilliardenlang durch’s Weltall flog, bis dann die Erde vor ca. 50.000 Jahren im Weg war.

Wissenschaftler nennen diesen Ort im uebrigen Barringer-Krater, weil der Herr Barringer der Erste war, der vorschlug, dass es sich bei diesem Krater um einen Meteoritenkrater handelt. Das United States Board on Geographic Names hingegen, benennt geografisch markante Punkte nach der naechstgelegene Postfiliale. Und diese heiszt „Meteor“. Denn mal ehrlich. Einen „Meteorkrater“ kann es eigentlich gar nicht geben. Høchstens einen Meteoritenkrater.

Aber hier nun endlich die Urinale:

Bei der Schuessel fuer kleine Menschen wollten die Erbauer mglw. erstmal ein normal hohes Urinal anbauen und ein Podest davor, damit besagte kleine Menschen ranreichen. Dann aber dachten sie sich vllt., dass es ja clever waere, die gesamte Schuessel tiefer anzubauen. Aber das Podest war da schon halb fertig.

Diese Extrakanten am Spuelkasten find ich interessant.

Und das war es nun mit dieser Miniserie. Ich habe erstmal keine weiteren Toiletten aus Bildungseinrichtungen (im allerweitesten Sinne). In der Zukunft kommen da sicherlich noch welche, aber die stehen dann wohl fuer sich.

… wenn man sich abseits der ueblichen Interessengebiete tummelt, ist schon erstaunlich. Und was man da alles erfaehrt ist schon sehr interessant. So zum Beispiel dieser lesenswerten, gar nicht so lange, Reisebericht ueber den Iran und dem widerspruechlichen Alltag einer saekularen Theokratie.

(Mal wieder) Via LeSpocky wurde ich auf einen interessanten Beitrag aufmerksam gemacht.

Dort aeuszert sich eine Frau ueber nicht unuebliche, ich befuerchte alltaegliche, Verhaltensweisen im „Technologiesektor“. Auch wenn ich derart schlimme Dinge nicht erlebt habe, so stimmen meine allgemeinen Beobachtungen im Wesentlichen mit dem ueberein, was dort steht: Hinter einem Schleier von „Hach was sind wir doch modern“ wird am Erhalt der Macht gearbeitet. Das heiszt also an patriarchalischen Strukturen, die alles was und jede(n) die/der anders ist, ausschlieszt.

So weit ist das ja eigentlich nichts Neues. Gut auf den Punkt gebracht fand ich aber dies:

I had for years and years of my past been whole-heartedly complicit in the systems of inequality and discrimination […]. I thought that if I made six figures and did well in my career, acted like „one of the boys” aka white male patriarchs, or played along with them, and was as vulgar, violent, self-centered and cut-throat as the „successful“ white men around me, that was „feminism“.

Ich verstehe darunter das (wenn auch gequaelte) Schmunzeln ueber den „Witz“ des Kollegen am Mittagstisch, dass Frauen nichts von Politik verstehen. Anstatt ihm ins Gesicht zu sagen, dass das eine ziemlich dumme Bemerkung ist.

I didn’t recognize my role in the tech industry as a privileged white woman, and didn’t do much of the internal and external work required to divest from those systems.

Diese Erkenntnis setzte bei mir irgendwann im Studium ein. Mglw. weil ich einen „armen sozialen Hintergrund“ habe, oder weil ich so viel mit einer anderen, diskriminierten Gruppe zusammen war – Schwulen und Lesben. Oder vielleicht habe ich ja auch die Dummheit dieser Strukturen von allein erkannt.
Das war ein Prozess, der mit Maeuseschritten vonstatten ging.

Dann geht es weiter mit:

As I started my political awakening, I was primarily concerned with the advancement of white women like myself and didn’t give much thought to broader systemic issues, or how I was complicit in the oppression of other groups.

Bei mir war es eben das „linke politische Spektrum“ bzw. Menschen, die mit „Willen und Leistung was aus sich machen“. Oder so wie sie es ausdrueckt:

My attitudes, beliefs and behavior were 100% born of my alignment with white capitalist patriarchy, and I benefitted enormously (And still do) from it […]

I […] [have] uncritically profited from white supremacy, cissexism, ableism, classism and other forms of oppression. My success, visibility, and achievements are fundamentally built on the oppression of others, and I spent years not giving a fuck, lending any semblance of a hand, acknowledging my role, or working to dismantle the systems I’ve been part of.

Und deswegen diese Artikel in meinem Weblog, denn …

Most of my privileges in life happen as a direct result of a white supremacist capitalist system, and I too long stayed silent and comfortable.

Mit diesem Bild der alten, und mittlerweile bestimmt renovierten, Toiletten aus dem Gebaeude 40 der Otto-von-Guericke Universitaet .oO(sind die Bindestriche richtig?) møchte ich euch, meine lieben Leserinnen und Leser, auf das Ende dieser Miniserie vorbereiten. Sind sie nicht schøn anzusehen:

Dieses Spiel der Farben, die Funktionalitaet der Komponenten.
Bitte beachtet die originalen, DDR-Urinal-Wasserhaehne! Die altehrwuerdigen Rohrleitungen. Und die noch sichtbaren Spuren, dass da mal andere Porzellanschuesseln montiert waren.
Ein wahres Prachtbild!

Nicht hinten Anstehen muss die Sitztoilette. Auch dort noch ein Originalspuelknopf. Hach! Der Rost! Ein Fest fuer die Glubschies!

Hierbei handelt es sich um eines der ersten meiner Kunstwerke. Erkennbar daran, dass der Toilettensitz oben ist. Da hatte ich also noch nicht meinen Toilettenfotografierstandard ausgearbeitet.

Beim naechsten Mal dann das letzte Bild in dieser Miniserie. Ich habe mir dafuer etwas gaaaaaaaaanz Besonderes aufgehoben :)

… dass das ja nur „bei denen“ so schlimm ist, aber nicht bei uns, der møge doch bitte diesen Artikel lesen.

Es steht ja eigentlich nichts Neues drin, aber es ist wichtig, dass wir das nicht aus den Augen verlieren.