Søren in Norwegen

Einen Computer was ausrechnen zu lassen hørt sich ja erstmal nicht so schwer an. Und ist es auch nicht mit so einer einfachen rekursiven Folge. Also programmierte ich das erstmal so geradlinig.

Und die einzelnen Elemente wurden immer laenger und laenger und mit ihnen die Folge.

Und auch die Analyse wie oft eine Zeichenkette vorkommt ist erstmal recht simpel:
– Nimm vom Anfang der Folge so viele Zeichen wie du brauchst.
– Welche Zeichenkette ist das?
– Setze den Zaehler fuer diese Zeichenkette um eins nach oben.
– Gehe in der Folge einen Schritt nach rechts und beginne von vorn.
Dabei dachte ich so, dass ich wenn ich das Vorkommen bspw. aller sechsstelligen Zeichenketten untersuchen will, dann sozusagen im Vorbeigehen auch gleich das Vorkommen aller fuenf-, vier-, drei-, zwei- und einstelligen Zeichenketten untersuchen kønnte. So schwer ist das nicht, wenn man sich naemlich im ersten Schritt die zu untersuchende Zeichenkette (bspw. mit sechs Zeichen) aus der Folge extrahiert hat, dann muss man von dieser Zeichenkette immer nur eins „abhacken“ bis nichts mehr da ist.

Ein Beispiel. Die Folge sei „1123581221“ und die Aufgabe sei alle Zeichenkette mit sechs Zeichen oder weniger zu untersuchen.
– Extrahiere die Zeichenkette „112358“ von der Folge.
– Schema F: der numerische Wert dieser Zeichenkette ist 112358; setze den Zaehler fuer diesen Wert um eins nach oben.
– Plan 9: Entferne von „112358“ das letzte Glied und erhalte die neue Zeichenkette „11235“; verfahre nach Schema F mit der nun 5-stelligen Zahl.
– Verfahre nach Plan 9 und erhalte die neue Zeichenkette „1123“; verfahre nach Schema F mit der nun 4-stelligen Zahl.
– Wiederhole dies so lange, bis die neue Zeichenkette nur noch ein Zeichen lang ist.
– Hacke nun von der ganzen Folge (!) das erste Glied ab und beginne von vorne.
– Dies ist so lange zu wiederholen, bis die gesamte Zeichenkette „verbraucht“ ist.

Durch dieses Verfahren vermeide ich eine doppelte Zaehlung bereits gezaehlter Zeichenketten, da beim naechsten Durchlauf durch die gesamten Schritte alles um eins nach rechts „verschoben“ ist und somit neue sechs- , fuenf-, vier- usw. -stellige Zeichenketten gebildet werden.

Ein Problem ergibt sich aus dieser Vorgehensweise: die Umwandlung der Zeichenkette in den numerischen Wert wandelt Zeichenketten mit fuehrenden Nullen in numerische Werte um, die die falsche (eine kleinere) Laenge haben. Aus der Zeichenkette „0007“ wird der Wert 7.
Dadurch wuerde also in diesem Falle bei den vierstelligen Zeichenketten einmal zu wenig und bei den einstelligen Zeichenketten einmal zu viel gezaehlt.
Eine Variation der Konsequenz ist, dass Zeichenketten die mehr als eine Stelle haben, erst dann gezaehlt werden, wenn das erste Zeichen keine Null ist.
Dreistellige Zeichenketten werden bspw. erst ab der 100 gezaehlt, vierstellige ab der 1000 usw. Dadurch werden 10% der Daten fuer x-stellige Zeichenketten nicht gezaehlt, bzw. falsch zugeordnet werden.

Beides kann man relativ brutal umgehen, indem man die Tabelle, in der die Haeufigkeit einer gewissen Zeichenkette gespeichert wird, massiv erweitert.
Anstatt (nur bis alle zweistelligen Ziffern) …

0	23 mal
1	12 mal
2	7 mal
…	…
98	11 mal
99	44 mal

… also eine erweiterte Tabelle:

einstellige Zeichenkette	Vorkommen		zweistellige Zeichenkette	Vorkommen
0	23 mal		00	5 mal
1	12 mal		01	1 mal
2	7 mal		02	18 mal
…	…		…	…
9	15 mal		09	23 mal
			10	99 mal
			11	3 mal
			…	…
			98	11 mal
			99	44 mal

Man beachte, dass die Werte fuer die Zeichenkette „1“ natuerlich anders sind, als fuer die Zeichenkette „01“.
Am auffaelligsten ist natuerlich, dass Erstere ca. 10 mal haeufiger Vorkommen sollte als Letztere. Es gibt ja 10 mal so viele zweistellige Zeichenketten, wie einstellige. Mit all diesen muss sich die spezifische Zeichenkette „01“ das Vorkommen „teilen“.

Der Vorteil dieser Methode: ich muss mir keinen Kopf mehr machen, dass der numerische Wert von „0007“ eine 7 ist. Ich teile dem Programm einfach mit, dass es gefaelligst in der Spalte fuer vierstellige Zeichenketten den Wert von Sieben um eins erhøhen soll und ich behalte in Erinnerung, dass es sich dabei eigentlich um die „0007“ handelt.
Oder anders ausgedrueckt: ich kann einfach die Umwandlung von Zeichenkette in numerischen Wert beibehalten und muss mir da nix extra ausdenken, wie ich dem Computer klarmache, dass fuehrende Nullen wichtig sind.
Dadurch wird natuerlich auch kein Wert einer weniger langen Zeichenkette mehrfach gezaehlt. Bei jeder x-stelligen Zeichenkette wird immer nur der Eintrag in der richtigen Spalte der Tabelle gemacht.

Zwei Nachteile hat diese Methode.
1.: Will ich das Vorkommen zweistelliger Zeichenketten anstatt nur einstelliger Zeichenketten untersuchen, erhøht sich mein Speicherplatzbedarf schlagartig um das zehnfache. Will ich dreistellige (und zwei- und einstellige) Zeichenketten untersuchen so brauche ich 100 mal mehr Speicherplatz, wie als wenn ich nur einstellige Zeichenketten untersuchen wuerde; usw. usf.
2.: Das Speichermanagement wird vermutlich einen signifikanten Teil der Rechenzeit beanspruchen. Mit jeder neu untersuchten Zeichenkette (also nach jedem „abhacken“ eines Zeichens), muss der Rechner zu einer ganz anderen Spalte in der Tabelle gehen, dort das richtige Element finden und den Zaehler um eins erhøhen. Der Rechner muss also auf x-vielen Tabellen gleichzeitig arbeiten und nicht nur auf einer.

Letztlich dachte ich mir aber, dass die Vorteile (das richtige Zaehlen und dass ich dem Programm nicht die Wichtigkeit fuehrender Nullen beibringen musste) die Nachteile ueberwiegen. Speicherplatz ist heutzutage wahrlich kein Problem und wie lange das Rumrødeln auf den Tabellen dauert … mhm … davon hab ich keine Ahnung, aber ich wollten den Rechner ohnehin viele Stunden rechnen lassen.

 

Soweit dazu.

 

Als ersten Versuch erstellte ich also ein Programm welches mir eine immer laenger und laenger werdende Zeichenkette erstellte. Wenn diese Zeichenkette eine bestimmte Laenge erreicht hat, so stoppte das Programm mit dem weiteren Hinzufuegen von Zeichen und  zerhackte diese Kette dann in kleine Stuecke und untersuchte diese.
Im ersten Satz erkennt man auch den Fehler dieses Programms. Oder weniger ein Fehler, als vielmehr den Grund, warum ich dieses Programm nicht fuer die eigentliche Arbeit benutzen konnte.

Auch wenn jetzt ein Experte sagen kønnte „das kommt auf die Codierung an“, so belegt im schlimmsten Fall eine 2-stellige Zeichenkette 2 Byte Speicherplatz. Eine hundert-stellige Zeichenkette also 100 Byte usw. Wenn ich also die Fibonaccifolge bis zur 10-milliardsten Stelle untersuchen will, dann belegt diese Folge im schlimmsten Fall 10 Gigabyte im Arbeitsspeicher.
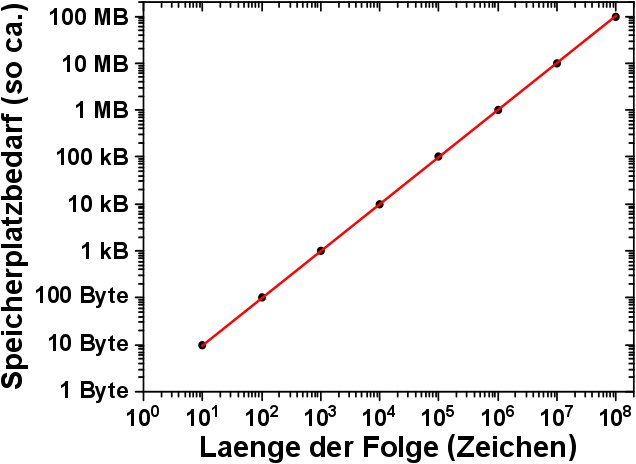
Weil ich grafische Veranschaulichungen so mag, hier eine eher sinnlose Darstellung dieses Sachverhaltes:

Tihihi … Man beachte bitte die doppellogarithmisch Darstellung. Der Speicherplatzbedarf nimmt also mit jeder Potenz der Laenge der Folge exponentiell zu. .oO(Hach wie schøn man einfache Zusammenhaenge doch unnøtig aufblaehen kann … Laenge der Folge in Abhaengigkeit von der Laenge der Folge … tihihi.)
In der Grafik ist der maximale Speicherplatzbedarf nur bis zu einer Fibonaccifolgenlaenge von 100 Millionen Zeichen dargestellt. Deswegen „sieht“ man noch nicht die oben erwaehnten 10 GB benøtigten Arbeitsspeicher. Meine Leserinnen und Leser møgen dies doch bitte selbst extrapolieren.

Ach so, der Speicher den die oben erwaehnte Tabelle braucht ist dagegen irrelevant.

Wieauchimmer, so viel Arbeitsspeicher habe ich leider nicht. Deswegen musste das Programm was das Erstellen der Zahl und einen Teil der Analyse angeht komplett umgeschrieben werden. Dazu aber im naechsten Artikel mehr.

Fuer dieses Mal ist festzuhalten: Ein Computer macht genau das was in den Anweisungen steht und erstmal nicht das, was man will, was der Computer machen soll. Deswegen muss man jedes noch so einfache Problem in kleine Schritt zerlegen und sich ueberlegen ob da nicht Sachen dabei sind, die der Computer dann genau so macht wie man es programmiert, die aber nicht der Løsung des Problems zutraeglich sind. Oder anders: man muss erstmal so dumm denken lernen wie ein Computer stupide das macht was man programmiert. Einen Teil dieses Prozess fuer diese spezielle Aufgabe habe ich hier dargelegt.