Parmanand Singh schreibt in der Historia Mathematica, Volume 12, Issue 3, August 1985, Seiten 229–244 in seinem Artikel „The so-called fibonacci numbers in ancient and medieval India“ (Volltext scheint fuer die Allgemeinheit verfuegbar zu sein), dass bereits Virahanka, Gopala und auch Hemachandra vor Leonardo da Pisa diese mathematische Folge von Zahlen und deren Bildungsgesetz angaben. Wohl auch in Europa war die Folge in der Antike bereits Nikomachos von Gerasa bekannt. Aber wie so oft, fallen Ruhm und Ehre wem anders zu, weil irgendwann mal irgendwer zu faul war ordentliche Literaturrecherche zu machen und hinterher will es wieder keiner gewesen sein und keiner gibt den Fehler zu und deswegen wird es bis heute nicht ordentlich gemacht. Aber letztlich ist’s ja doch auch nicht so richtig relevant, was fuer einen Namen das Kind traegt … wohohoho … DAS ist natuerlich eine ganz andere Diskussion im Zusammenhang mit wirklichen Kindern; aber darum soll es hier nicht gehen. Deswegen halte ich mich an diesen nach dem „filius Bonacii“ (Sohn des Bonacii) gegebenen Namen.
Die Fibonaccifolge ist eine so schøn einfache Folge. Das naechste Element bildet sich aus der Summe der ersten beiden Elemente. Aus 1 und 1 mach 2. Aus 1 und 2 mach 3. Aus 2 und 3 mach 5. Aus 3 und 5 mach 8 usw. ad infinitum. Hier sind mal die ersten Glieder:
1, 1, 2, 3, 5, 8, 13, 21, 33, 54, 87, 141, 228, 369, 597, 966, 1563 … … …
Diese Reihe waechst also relativ rasant.
Die Zahlen alle hintereinandergeschrieben ergeben eine neue Zahl. Im obigen Beispiel waere das 11235813213354871412283695979661563. Bis zum 17. Element „bildet“ die Fibonaccifolge eine 35-stellige Zahl.
Alles klar, alles einfach. Ich erzaehle das, um das anstehende Problem besser zu verdeutlichen.
In kurz (und mathematisch nicht ganz sauber formuliert) beschaeftigte mich seit Jahren der Gedanke, ob alle Zahlen gleich haeufig in der Fibonaccifolge vorkommen.
Oder anders: wie oft kommt mein Geburtsdatum in der Fibonaccifolge bis zur 100-millionsten Stelle vor und kommt jede andere achtstellige Zahl genauso haeufig vor.
AHAHAHA! In der zweiten Formulierung steckt schon etwas korrektere Mathematik – die Haeufigkeit einer Zahl.
Natuerlich kommen nicht alle Zahlen gleich oft vor bis zu einer gegebenen Stelle der Folge.
Zur Veranschaulichung denken wir uns 4-stellige Zahlen; bspw. die 1234 oder die 9999. Dann kann es natuerlich schon sein, dass die 1234 bis zu einer bestimmten Laenge der Folge exakt genau so oft drin ist, wie die 9999, oder die 8765. Aber von allen 4-stelligen Zahlen wird sicherlich die eine oder andere øfter oder weniger oft bis zu dieser Stelle der Folge drin sein.
„Genauso haeufig“ wuerde also auf die Frage hinaus laufen, ob das Vorkommen aller Zahlen bis zu einer gegebenen Laenge der Fibonaccifolge normalverteilt ist.
Und hier kønnte ein richtiger Mathematiker mich verbessern. Zum Ersten gibt es es einen ganzen Haufen von Wahrscheinlichkeitsverteilungen. Ich habe nicht die leiseste Ahnung, ob die Normalverteilung die Richtige ist (sein kønnte). Bei der Wahl der Verteilung folgte ich dem Indifferenzprinzip (und dem Einfachheits- bzw. Faulheitsprinzip: keine Ahnung haben = nimm das was du kennst).
Zum Zweiten ist die Normalverteilung eine stetige Wahrscheinlichkeitsverteilung. Bei dem Problem handelt es sich aber um ein „diskretes Problem“. Ich sollte das also dahingehend umformulieren, ob sich das Vorkommen aller Zahlen einer Normalverteilung angleicht. Ich habe aber wiederum keinen blassen Schimmer inwiefern das gerechtfertigt ist (sein kønnte).
Das erinnert mich etwas daran, dass ich erstmal zeigen sollte, dass es eine Løsung gibt bevor ich mich an das Berechnen dieser Løsung mache.
Wieauchimmer, mich duenkt, dass dieses Problem mit dem Problem verwandt ist, ob eine Zahl normal ist. Auch bei dieser Behauptung bleibe ich mir (und euch, meinen lieben Leserinnen und Lesern) den Beweis der Richtigkeit derselben schuldig.
Im uebrigen ist das bei Pi (und anderen irrationalen Zahlen) eine offene Frage. Bis zur 100-millionsten Stelle scheint es aber wohl ganz gut zu passen.
Das Problem laeszt sich also auf zwei einfache Probleme herunterbrechen:
1.: addiere zwei Zahlen nach einem bestimmten Schema und haenge die Summe an die Kette ran; brich ab, wenn die Kette eine bestimmte Laenge hat;
2.: zaehle wie oft gewisse Zahlen vorkommen.
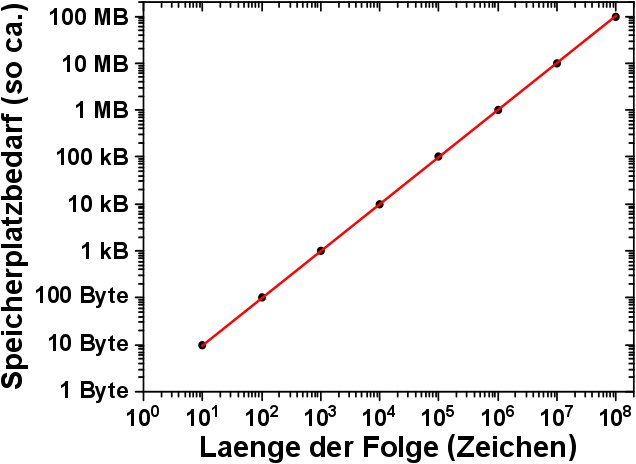
„Einfach“ in so fern, dass man sich das leicht vorstellen kann. Am Beispiel oben sieht man ja aber, wie rasant die einzelnen Elemente wachsen. Zur Addition wuerde ich also einen Computer empfehlen. Und eine Zahl mit 100 Millionen stellen zu untersuchen ist auch recht langwierig. Da der Computer ohnehin schon zur Hand ist, sollte der gleich auch zur Analyse benutzt werden. Schlieszlich handelt es sich um ein Zahlenverarbeitungsproblem. Dafuer wurden die Dinger schlieszlich erfunden.
Eigentlich greife ich mit all diesen Ausfuehrungen schon viel zu weit vor. Ich war ja dabei, dass mir das Problem seit Jahren im Kopf rumspukte. Ich hatte aber nie die Musze, mich da mal naeher mit zu beschaeftigen. Wusste ich doch, dass ich dafuer zumindest rudimentaere Programmierkenntnisse haben muss.
Dann aber geschah es, dass ich vor einiger Zeit bei einem Quiz dabei war. Ich will jetzt nicht sagen, dass ich „mitgeschleppt“ wurde. Ich bin da aus eigener Initiative mitgegangen. Aber mein Wissen zu norwegischen Gerichten, Werbespruechen oder anderen bei solchen Quiz‘ gefragten Sachen halten sich doch sehr in Grenzen.
Ich hatte aber einen Stift in der Hand und eine Serviette vor mir liegen. Zunaechst malte ich nur die ueblichen Krusedull (ein Wort, welches ich sehr sehr toll finde). Etwas im Geiste finge ich dann an, die ersten Elemente der Folge aufzuschreiben. Dann begann ich noch mehr Elemente ordentlich auszurechnen. Ich schrieb die Folge bis zu einer gewissen Laenge auf (mich duenkt bis zur 39. Stelle oder so) und zaehlte, wie oft die Zahlen 0 bis 9 darin vorkamen. Dannn zeichnete ich ein Histogramm.
Und dann geschah das, was i.A. als Nerd-Sniping bekannt ist. Ich fing an mir mit meinen (mittlerweile vorhandenen) rudimentaeren (wirklich nicht mehr!) Programmierkenntnissen Gedanken ueber eine Automatisierung des Ganzen zu machen. Nebenbei lief das Quiz natuerlich weiter und ich warf auch ab und zu mal ein Kommentar ein.
Hier ist die Arbeit des beschriebenen Abends zu sehen:
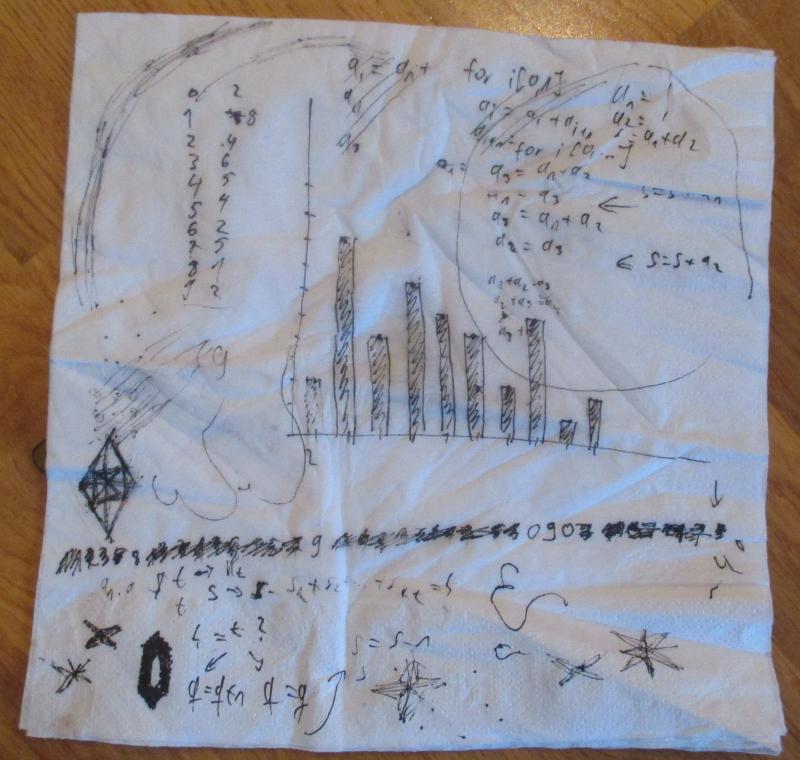
Damit løse ich natuerlich nicht das eigentliche mathematische Problem dahinter. Aber ich sage mal so. Wenn ich sehe, dass sich die Haeufigkeiten fuer bspw. alle vierstelligen Zahlen bis sagen wir zur 100-millionsten Stelle der Fibonaccifolge einer Normalverteilung genuegend angleichen, dann sehe ich das Problem fuer meine Beduerfnisse als geløst an.
Eine technische Sache noch an dieser Stelle. Bisher schrieb ich bspw. „4-stellige Zahlen“. Natuerlich sind damit 4-stellige Zeichenketten gemeint.
4-stellige Zahlen beginnen bei der 1000 und enden mit der 9999.
Bei der „0007“ hingegen handelt es sich um eine 4-stellige Zeichenkette, auch wenn die Zahl selber einstellig – die Sieben eben – ist.
Wenn man sich auf die Ziffern 0 bis 9 als Zeichen beschraenkt beginnen 4-stellige Zeichenketten bei der „0000“ und enden bei der „9999“. Man hat also insgesamt 10.000 verschiedene 4-stellige Zeichenketten.
Ich entdeckte dieses Problem erst als ich schon „mittendrin“ war. Sicherlich auch dadurch bedingt, weil ich die ganze Zeit ja irgendwie mit Zahlen arbeite. Da musste ich durch „Fehler in den Resultaten“ erstmal auf den Unterschied zwischen Zahl und Zeichenkette gestoszen werden.
Aber genug fuer heute.
Die naechsten Beitraege werden sich zunaechst dem „technischen Hintergrund“ widmen, bevor ich mich an die Dartellung der spannenden (und schønen) Ergebnisse mache.