Søren in Norwegen

Olavs Pub ist hier gleich neben dem Nova Kino. Und das Nova Kino kenne ich ganz gut. An manchen Tagen im Jahr verbringe ich da mehr Zeit als zu Hause.

Ich muss aber sagen, dass ich dort noch nie speiste oder trank. Zumindest kann ich mich nicht erinnern. Also im Pub, nicht im Kino. Also da ja sowieso nicht. Ist ja ein Kino und kein Platz zum lustigen Beisammensein! Wo kaemen wir denn da hin!

Ganz toll, wie mir das Stehklo begegnete:

Mal von den schønen Fliesen abgesehen, scheint dort wer kurz vorher ein bisschen zu feste gefeiert zu haben. Aber naja, Scherben bringen Glueck. Und zum Polterabend haben wir frueher auch Waschbecken geschleppt.

Zunaechst interessant ist diese „Black Box“, die offensichtlich Chemikalien ins Wasser leitet. Aber ich mag den sprøden Charme von Urinsteinen lieber.

Das Sitzklo wurde aufgehuebscht von Gaesten:

So muss das sein! Pappt die Aufkleber dahin wo Platz ist, bekritzelt die Waende und hinterlasst das Klo so, wie ihr es selber gerne vorfinden wuerdet.

WATT? WIE? Ich putz hier doch nicht! … *lacht*

Nachdem das Religionsbedürfnis aber anthropologisch ein solides Fundament aufzuweisen scheint, ist ein Ende dieser Emanationen geistiger Schlichtheit leider nicht absehbar.
(von hier)

Die Kunst zu beleidigen, ohne dass es sofort so aufgefasst wird … tihihi.

Den Heisenberg hatten wir ja neulich schon. Da bietet es sich natuerlich an zu zeigen, dass seine Wirkstaette auch auf meinem Arbeitsweg liegt:

Tihihi

Und nein! Keine Links fuer die Banausen an dieser Stelle. Immer nur Løten … da wird man doch bekloppt!

Es wird so oft in einigen Teilen „meiner Kreise“, immer auch etwas abschaetzig, rueckstaendig und unmodern meinend, als „totes Holz“ bezeichnet. Sei’s drum.

Das Buch ist aber nicht nur Lesestoff oder Informationsquelle. Durch das Umblättern der Seiten, den teilweise muffigen Geruch alter Bücher, das Wissen darum, wie viele Jahre so ein Werk bereits überdauert hat, wird das Lesen zu einem Erlebnis für alle Sinne.

Eine kleine Insel im Fjord. Wobei die waehrend der Eiszeit sicherlich unter Wasser lag und damit (noch) keine Insel war. Also unter festem Wasser natuerlich. Sehr viel festem Wasser. So ca. 1000-1500 Meter unter Wasser lag die Insel (siehe hier oder hier).

Aber das meinte ich nicht. Ich meinte, wenn all das feste Wasser damals nicht auf Norwegen gelegen und dieses wunderschøne Land heruntergedrueckt haette, dann waere die Oberflaeche von Munkholmen unter Wasser gewesen.

Anderseits, wenn all das feste Wasster einfach nur nicht da gewesen waere, also auch nicht im fluessigen Zustand, dann waere der Meeresspiegel natuerlich viel niedriger und ich wuesste nicht, ob meine obige Aussage noch gelten wuerde.
Aber wenn wir mal annehmen, dass eine wieauchimmer geartete Entitaet in der Lage gewesen waere innerhalb kurzer Zeit, sagen wir mal 100 Jahre, aber 1 Tag fetzt natuerlich mehr, genuegend Energie zuzufuehren kønnte, um all das feste Wasser zu schmelzen, dann … … … uiuiui … ueberschlagen wir das mal kurz …Erstmal ein paar vereinfachende Annahmen.

Die Dicke des festen Wassers wird als homogen angenommen und die Zahl setze ich auf den Wert auf Trondheimhøhe – 1500 Meter. Was im Uebrigen relativ genau der Haelfte der maximalen Dicke des damals real existierenden festen Wassers entspricht.
Das geht, wenn man ein lineares Dickenprofil des festen Wasser annimmt. Also duenn im Sueden und dick im Norden. Das ist natuerlich ad hoc um’s mir hier einfacher zu machen. Rein intuitiv kønnte ich mir denken, dass das richtige Profil sowohl eher eine logarithmische als auch eine exponentielle „Form“ gehabt haben kønnte. Aber ich kønnte nicht schluessig begruenden warum. Und „nur so ein Gefuehl“ hørt sich fuer mich schlimmer an als „ad hoc“.

Die vom festen Wasser bedeckte Landflaeche ist recht genau bekannt – 32 Prozent.

Bei einem Erdradius von ca. 6400 km, wobei 71 % von fluessigem Wasser bedeckt sind, macht das ca. 7500 von festem Wasser bedeckte Quadratkilometer.

Meerfestwasser muessen wir nicht beruecksichtigen, da es ja nicht wirklich beitraegt zur Erhøhung des Meeresspiegels.

Trotz der massiven Ausdehnung des festen Wassers, muss ich die (ungefaehre) Kugelform der Erde hier nicht in Betracht ziehen, weil ja sowohl die Unter- als auch die Oberseite der Gravitation folgten.

Unter den obigen Annahmen folgt daraus, dass ca. 10¹⁶ g – 10 Petagram oder gern auch 10 Pg – festes Waser zu schmelzen sind.

Wie wir ja schon aus der Schule wissen, ist die benøtigte Energie um einen Stoff zu erwaermen abhaengig von der spezifischen Waermekapazitaet.
Bei festem Wasser ist dieser Wert relativ stark temperaturabhaengig. Ich nehme an, dass das feste Wasser keine Temperatur von -100 Grad Celsius hatte. Ad hoc lege ich den Wert auf -20 Grad Celsius fest (ich hab da so’n Gefuehl … *lacht*) und die spezifische Waermekapazitaet betraegt dann ca. 2,06 kJ pro kg und Kelvin.
Das bedeutet, man muss ca. 40 kJ Energie zufuehren um 1 kg festes Wasser von -20 Grad Celsius auf null Grad Celsius zu erwaermen.
Und nun haben wir immer noch festes Wasser, nur dass das jetzt waermer ist.

Die Schmelzwaerme von Wasser betraegt 333,5 kJ pro kg.
Holy mackerel! Um das selbe Kilogramm Wasser nun zu schmelzen benøtigt man also fast zehn mal so viel Energie.
Oder anders: wenn man so viel Energie zufuehren kann, um das viele feste Wasser in den fluessigen Aggregatzustand ueberzufuehren, dann muss man sich sicherlich um die Energie fuer die zuvor zu erfolgende Temperaturerhøhung des festen Wassers keine Sorgen machen.

Mit diesen Werten kann ich jetzt behaupten, dass die oben angenommene Entitaet ca. 3,5 mal 10¹⁸ kJ – 3,5 Exajoule oder gern auch 3,5 EJ – dem festen Wasser zufuehren muss, um es zu schmelzen.

Wie kønnte man nun diese Energie zufuehren?
Als erstes faellt einem natuerlich ein (oder eine Million) Laser ein. … *ein leises, leicht entruecktes Kichern ist zu høren* … tihihi

Schauen wir uns doch mal an, wie Wasser elektromagnetische Strahlung absorbiert, damit wir die Eigenschaften der Laser optimieren kønnen.

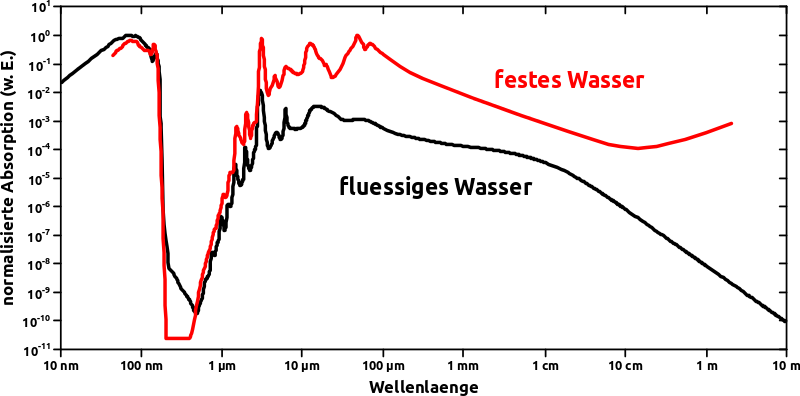
Dieses Bild zeigt die Absorptionskurve fuer elektromagnetische Strahlung von festem (rote Kurve) und fluessigem Wasser (schwarze Kurve).
Man beachte, dass es sich um eine doppellogarithmische Darstellung handelt.
Die Daten fuer festes bzw. fluessiges Wasser kønnen hier und hier gefunden werden.
Fuer festes Wasser fand ich dazu auch einen Artikel. Fuer fluessiges Wasser sind diese wohl aus: D. J. Segelstein, „The complex refractive index of water,“ University of Missouri-Kansas City, (1981). Das habe ich aber nicht ueberprueft.

Zunaechst faellt auf, dass sich das Absorptionsverhalten von festem und fluessigem Wasser sehr aehnelt.
Das ist nicht so toll, denn das feste Wasser soll ja geschmolzen werden und nicht das gerade fluessig gewordene Wasser aufgewaermt. Gluecklicherweise kommt da ein anderes Naturphaenomen zu Hilfe: Gravitation. Das fluessige Wasser flieszt einfach ab. Gut wa!
Die Unterschiede bei groszen Wellenlaengen kønnten ausgenutzt werden. Allerdings ist die Absorption dort vier oder mehr Grøszenordnungen geringer, als bei anderen Wellenlaengen. Deswegen betrachtete ich dies nicht weiter. Nuetzt ja schlieszlich auch nichts, wenn das fluessige Wasser zwar nicht so stark aufgewaermt, das feste Wasser aber auch nicht geschmolzen wird.

Im Weiteren wird nur noch die Absorptionskurve des festen Wassers betrachtet.
Bei sehr kleinen Wellenlaengen ist die Absorption i.A. grosz. Das merken wir uns fuer spaeter.
Es gibt mehrere markante Linien in der Absorptionskurve. Relevant sind die bei ca. 3 µm, 12 µm und 47 µm. Das merken wir uns auch fuer spaeter.

Um die Verfilmung dieses Ereignisses noch spektakulaerer zu machen als es an sich schon ist, postuliere ich, dass die Entitaet diese vielen Laser im Weltraum positionieren wird. Ist ja auch praktischer.

Das bedeutet aber, dass die Opazität (Absorption und Streuung) in der Atmosphaere beruecksichtigt werden muss.
Dazu habe ich leider keine zusammenhaengenden Originaldaten gefunden. Alles was ich fand waren nur Ausschnitte in kleinen Wellenlaengenbereichen.
Die NASA hat aber diesen schønen Plot erstellt. Nach zwei Tagen Sucherei und absolut keiner Lust, die Kurve aus den vielen Verøffentlichungen zusammenzustueckeln, da dachte ich mir: „NASA … ach der kønnen wir schon mal unhinterfragt alles glauben, nicht wahr“.

Hier ist der fuer meine Zwecke angepasste Plot .oO(Public Domain ist schon was Feines):

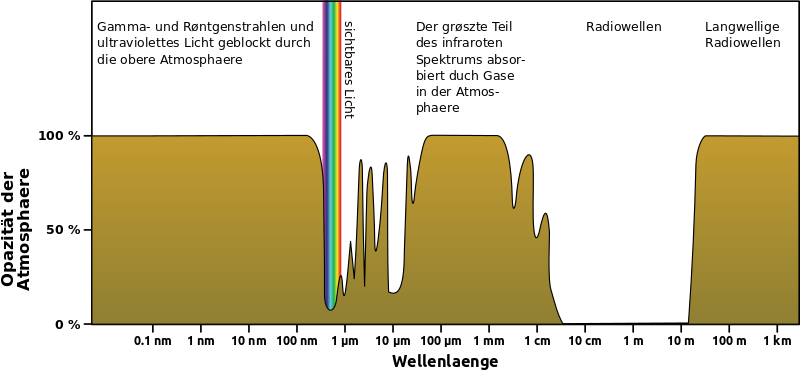
Wir sehen die Opazitaet der Atmosphaere, welche umgekehrt proportional ist zur Durchlaessigkeit (fuer die jeweilige Wellenlaenge).
Eine hohe Opazitaet bedeutet also, dass die jeweilige Strahlung nicht durch kommt.
Ein Glueck, dass dies fuer kleine Wellenlaengen gilt.
Damit ist aber die Idee einen Gammastrahlenlaser zu benutzen leider dahin :(. … … … .oO(Gammastrahlenlaser … wie geil! *lacht* … ich mach doch immer noch die besten Gags selber)

Das „optische Fenster“ zwischen ca. 2 cm und ca. 15 m bietet sich erstmal an. Aber zum einen ist da die Absorption des festen Wassers nicht mehr so gut (siehe Bild oben) und zum anderen sollte die Erde lieber nicht auch noch als Mikrowellenofen herhalten muessen.

Schauen wir uns den Bereich um die drei oben erwaehnten, markanten Linien etwas genauer an.

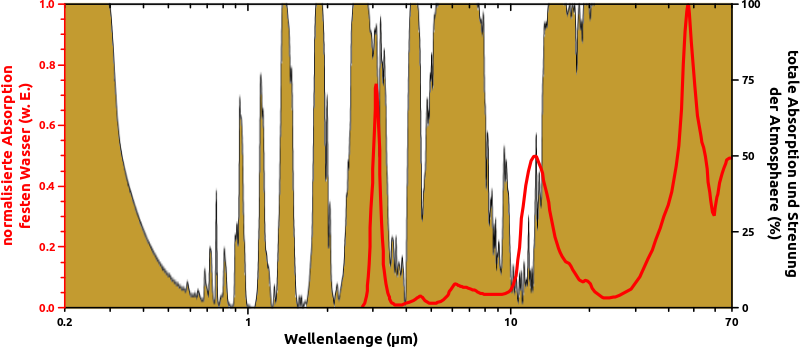
Hier zu sehen ist die bekannte Kurve des Absorptionsverhaltens festen Wassers (rot) aus dem Bild weiter oben, im Wellenlaengenbereich zwischen 0,2 µm und 70 µm. Liebe Leserinnen, liebe Leser, bitte beachtet, dass die Absorption jetzt linear dargestellt ist. Die linke Ordinate ist die fuer diese Kurve zu Gebrauchende.
Im Hintergrund ist die totale Absorption (und Streuung) der Atmosphaere dargestellt. Die rechte y-Achse ist fuer diese Kurve zu gebrauchen.
Das Bild habe ich schamlos geklaut.

Auch hier gestaltete sich die Suche nach Rohdaten als letztlich dann zu aufwendig. Die Absorption und Streuung in der Atmosphaere ist naemlich verdammt kompliziert, weil das alles abhaengig ist von den verschiedenen Gasen, Druecken, Temperaturen und was weisz ich noch alles.
Aber diese Gestalt der Kurve begegnet einem øfter, wie bspw. hier, oder hier, oder hier, oder hier. Und auch an anderen Stellen. Ich hoffe meine Leserinnen und Leser nehmen mir es nicht all zu uebel, dass ich deswegen nicht weiter nach Originaldaten suchte.

Leider muss festgestellt werden, dass ausgerechnet die prominentesten Linien bei 3 µm bzw. 47 µm vollstaendig auch von der Atmosphaere absorbiert werden.
Mhm … hat ja auch was Gutes, denn damit liegt die Laserwellenlaenge fest: 12 µm.

Das Licht wird zwar ein paar Mikrometer weiter eindringen in das feste Wasser, aber dieses ist ja so dick, dass letztlich doch alles absorbiert wird.
Wir brauchen also keine høhere Laserleistung.
Ach was rede ich denn hier???
SELBSTVERSTAENDLICH brauchen wir eine høhere Laserleistung! Und mehr Laser! VIEL MEHR Laser … MUAHAHAHAHAHA.

Bei einer Wellenlaenge von 12 µm ist das Spektakel leider nicht zu sehen *weep*.
In der Multi-Milliarden-Dollar-Verfilmung werden wir da aber groszzuegig drueber hinwegsehen.
Auszerdem duerften aufgrund der benøtigten Leistung der Laser Ionisierungseffekte in der Atmosphaere auftreten. Wir koennen also doch alles sehen.
Was das fuer die Absorption der Laserstrahlung bedeutet, werde ich an dieser Stelle nicht diskutieren. Stellt euch einfach vor, dass das keinen Unterschied macht … *Bauchschmerzen bekomm*

Apropos Laserwellenlaenge. Wenn wir nicht auf eine wieauchimmer geartete Entitaet warten wollen, so kønnten wir das mit vorhandener Lasertechnologie auch heute schon realisieren. Kohlenstoffdioxidlaser strahlen zwar bei 10,6 µm (was einer weiteren Verminderung der Absorption im festen Wasser um ca. den Faktor drei bedeuten wuerde), aber es sind die Laser mit den heutzutage høchsten realiserbaren Leistungen im Dauerstrichbetrieb.
.oO(Mhmmmm … das bringt mich auf eine Idee … brauch ich blosz noch jemanen, der mir das finanzieren wird) … MUAHAHAHAHAHA.

Nun zur bereits erwaehnten Leistung der Laser.

3,5 EJ muessen innerhalb eines Tages darnieder ins feste Wasser gebracht werden. Das sind 10¹⁴ Wh – 0,1 Petawattstunden oder gern auch 0,1 PWh.
Bei einer Million Lasern entspricht das einer Leistung von 4 MW pro Laser.

Megawattlaser … Ist das realistisch? … *hust*.
Oder wir nehmen handelsuebliche CO₂-Laser wie bspw. diesen hier, der eine Leistung bis 10 kW hat.

Da braeuchten wir dann zwar 4 Milliarden von, aber mehr Laser … das ist immer gut.
Diese Zahl verdopple ich mal lieber und runde auf zur naechsten Grøszenordnung. Ist immer wichtig! Um bspw. auf der sicheren Seite zu sein bzgl. solcher Dinge wie Ausfall, Schwankung in der Leistung, Erringung der Weltherrschaft etc. pp.
Also wir (wie immer, das Kønigliche) braeuchten nur 10 Milliarden handelsuebliche CO₂-Laser um all das feste Wasser zu schmelzen, welches in der letzten Kaltperiode auf den Landflaechen lastete.

Kleine Notiz am Rande: die radioaktiven Prozesse im Erdkern haben eine konstante Leistung von ca. 3,5 TW.
Der geneigte Leser møge den interessanten Rest selbst ausrechnen.

Aber ich schwoffte ab.

Auf Munkholmen gibt es eine Art „Stube“, wo man auch was Essen und Trinken kann. Auszerdem gibt es dort auch Toiletten, die auch von den Besuchern dieser Staette benutzt wird.
Und das Urinal ist gar wunderschøn anzusehen:

Hach … diese schicken Abflussrohre, Fliesen und „Frischesteine“. Auch die Form des Urinals passt dazu. Und zwei unterschiedliche Spuelknøpfe. Da kønnte man glatt auf die Idee kommen, dass sich da jemand mal Gedanken gemacht hat.

Auch das Sitzklo passt sich gut ein.

Insbesondere die Klobrille. Wobei natuerlich die schicken Details etwas fehlen. Aber da sind Urinale ja ohnehin im Vorteil.

Eine Metabemerkung zum Abschluss.

Ich hoffe dass ihr, meine lieben Leserinnen und Leser so viel Freude beim Lesen dieses Artikels hattet, wie ich beim Schreiben.
Erst dachte ich, dass es schnell geht, wie eigtl. fast alle Artikel in dieser Kategorie. Aber dann hatte ich so ’ne Idee … und dann war ich drei Tage mit recherchieren, Daten aufarbeiten und diskutieren beschaeftigt.
Das fetzt zwar, aber bei dieser Rate an geschriebenen Artikeln, wuerde es ewig dauern euch, meiner lieben Leserschaft, alle meine Toilettenbilder zu praesentieren.

Mehr aus dem neulich empfohlenen tollen Interview:

I bawled [my sister] out one time for not doing more with the talents she had. She replied that having talent doesn’t carry with it the obligation that something has to be done with it.

So einfach ist das also mit den anarchistischen Prinzipien.
Ganz im Gegensatz zum herrschenden Arbeits“ethos“:

This was startling news to me. I thought people were supposed to grab their talents and run as far and fast as they could.

Wie bereits angekuendigt, eine noch fetzigere Umsetzung des perfiden Fliegentricks:

Endlich mal ein Tor, welches sogar die Amerikaner treffen kønnen. … … … Nicht, dass ich Ahnung davon haette, wenn 20 erwachsene, aber offensichtlich bekloppte, Menschen hinter ’ner Kugel herlaufen um die in einen Kasten zu beførdern. Wo dann zu allem Unfug auch noch jemand steht, der diesen armen Menschen ihren Spasz verderben will. Und ich will ueberhaupt erst gar nicht von den zahlreichen Oberbescheuerten anfangen, die sich das sogar nur anschauen und nicht mal dran teilnehmen.

Irgendwie fuehle ich mich jedes mal etwas an diesen immer wieder sehenswerten Klassiker erinnert. (Ich hoffe ihr duerft das auch sehen, dort bei euch, in Zensurhausen).

Weil damit das Niveau so schøn gehoben ist, und weil beim Schreiben dieses Artikels diese unsaegliche „wm“ noch im Gange ist, gleich noch ein Kommentar von Ian Buruma in The New York Review of Books vom August 2005 (via):

In Europe, where overt nationalism has become a taboo since the great wars of the last century, soccer games are now almost the only focus of chauvinist mass hysteria.

Das Zitat ist zwar _vøllig_ aus dem Zusammenhang gerissen, aber wer mag da schon widersprechen?

Wieauchimmer, O’Learys ist eine „Sportbar“. Die als Pommesdip missbrauchte Hamburgersausze ist recht lecker ab und an. Und solange man es nicht zu oft isst, schmeckt auch der vegetarische Cesarsalat recht passabel.

Das Pissoir gefaellt mir ganz gut muss ich sagen. Wieder: passend. Wieviel so gewisse farbige Fliesen und so ein Gimmick im Pissbecken schon ausmachen kønnen.

Beim Bild des Sitzklos gefaellt mir die Unschaerfe … ob Heisenberg hier mal strullern war … tihihi … doppelt lustig … aber mich duenkt, dass nur der kleine Mann auszer mir auch den zweiten Gag versteht … und die Form der Spuelknoepfe … so schøn unsymmetrisch.

Auch die Fliesen an Wand und Boden laden ein zum Verweilen (nicht, dass man eine Wahl haette, aber ich wollte das schon immer mal in diesem Zusammenhang schreiben).

Es braucht also gar nicht viel um ein Klo gut zu gestalten.

Aus dem neulich empfohlenen tollen Interview:

You know what H. L. Mencken said one time about religious people? He said he’d been greatly misunderstood. He said he didn’t hate them. He simply found them comical.

… tihihi:

Neulich (Februar 2012) las ich am Zeitungsstand dies:

Uebersetzung: „Wir sind so gierig auf Grandiosa [Anm.: Norwegens Favoritpizzamarke], dass 30 mehr in der Fabrik angestellt werden muessen.“

Sogar etwas wichtiger war (da auf den Seiten 26 und 27, also noch vor der Pizzageschichte), dass Frauen in jeder vierten Beziehung mehr verdienen als der Mann.

Groszartig, nicht wahr!
Ich finde dieses Land – Norwegen – einfach toll.

Es sind zwar auch nur Babyschritte aus dem jahrtausendealten Dreck hinaus, aber wenigstens geht man diese. Und sollte ich doch irgendwann nochmal ’ne Tochter haben, dann wird diese mglw. doch mal in einer besseren Welt aufwachsen.